gamma分布简介
大写:Γ
小写:γ
Gamma 函数在概率统计中频繁现身,众多的统计分布,包括常见的统计学三大分布(t 分布,χ2 分布,F分布)、Beta分布、 Dirichlet 分布的密度公式中都有 Gamma 函数的身影;当然发生最直接联系的概率分布是直接由 Gamma 函数变换得到的 Gamma 分布。
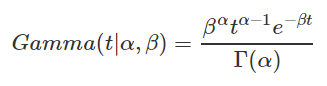
θ=1/β称为scale parameter,同样决定曲线有多陡。
固定 =4,可以看到随着θ参数的增加,x轴的scale在增加,其分布相对就越广。若放在同一个x轴上,增加θ将得到更平缓的曲线(相应地,y轴的scale减小)。

固定α=4,随着β参数的增加,x轴的scale在减小,其分布相对就越窄。若放在同一个x轴上,增加β将得到更陡的曲线(相应地,y轴的scale增加)。
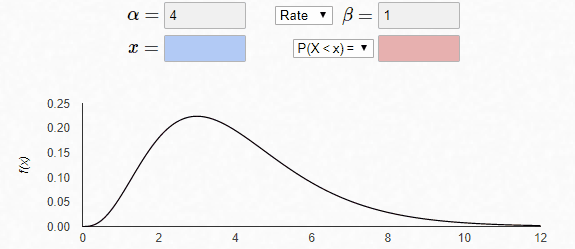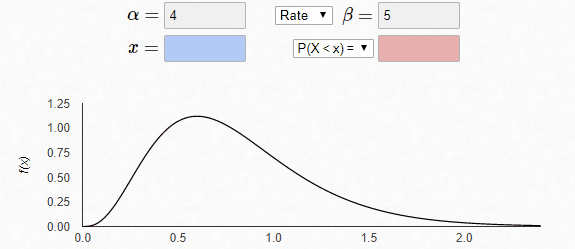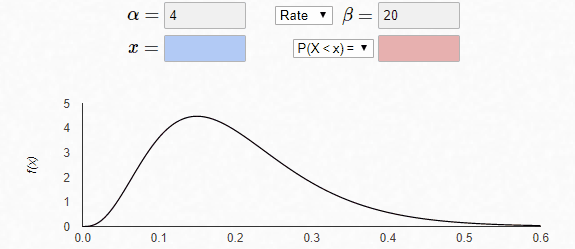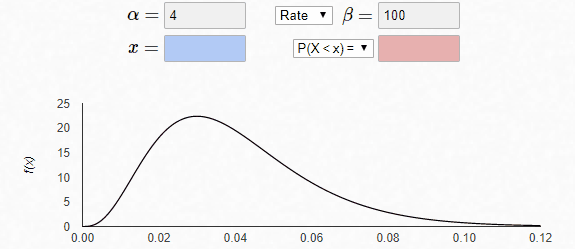
最后,固定β=1,α改变,曲线的形态发生改变
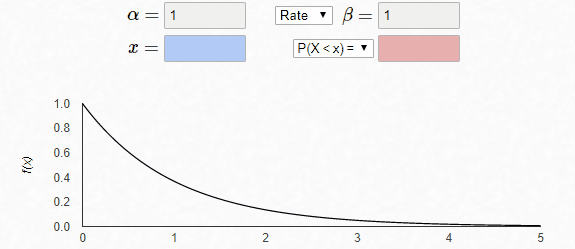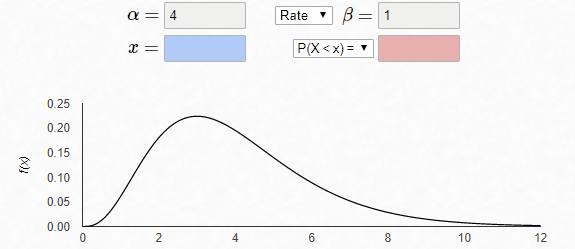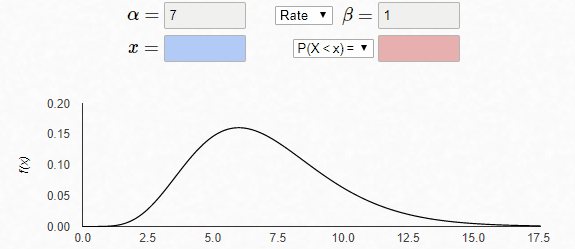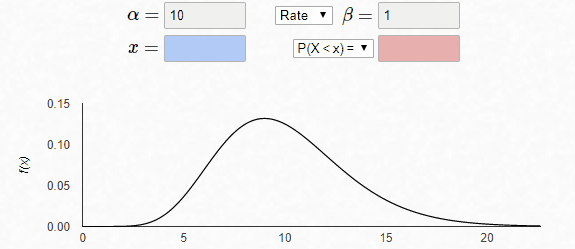
gamma相关函数
这几个R中的函数d-/p-/q-/r-,把gamma换成binom就成了binomial分布相关的计算,换成norm就成了normal分布的计算。gamma的函数,你不一定能用上,但是norm相关的几个函数肯定是会用得到的。
# 概率密度函数值 pdf# 算的是某一个点上的概率密度。dgamma(x, shape, rate = 1, scale = 1/rate, log = FALSE)# 概率分布函数值 cdf 累积概率pgamma(q, shape, rate = 1, scale = 1/rate, lower.tail = TRUE,log.p = FALSE)# 概率分位函数值qgamma(p, shape, rate = 1, scale = 1/rate, lower.tail = TRUE,log.p = FALSE)# 产生服从伽马分布的随机数rgamma(n, shape, rate = 1, scale = 1/rate)
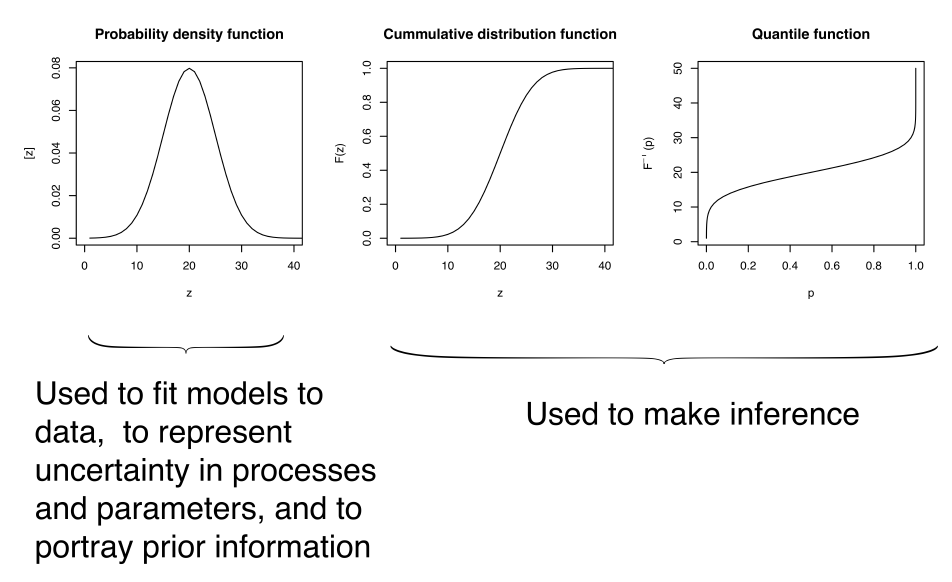
pdf和cdf
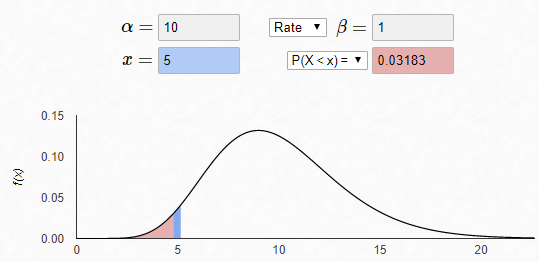
pgamma给定一个值计算累计概率
R: pgamma(5,10,1,lower.tail = T)
Matlab: gamcdf(5,10,1)
[1] 0.03182806
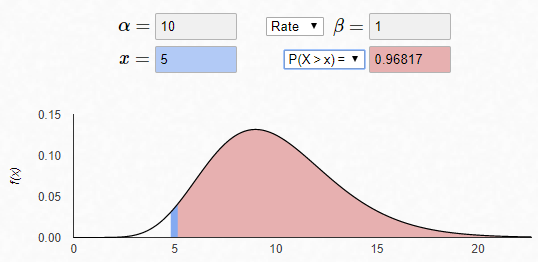
R: pgamma(5,10,1,lower.tail = F)
Matlab: gamcdf(5,10,1,'upper')
[1] 0.9681719
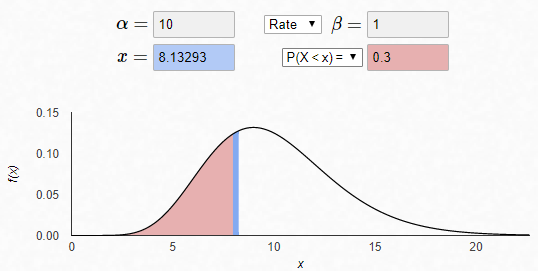
qgamma给定累计概率计算对应的值(相当于找cutoff)
R: qgamma(0.3,10, lower.tail=T)
Matlab: gaminv(0.3,10,1)
[1] 8.132928
R: qgamma(0.3,10, lower.tail=F)
Matlab: gaminv(0.7,10,1)
[1] 11.38727

gamma和inverse gamma
set.seed(1)1/rgamma(n=1, shape=10,scale=1/2)[1] 0.2608497set.seed(1)rinvgamma(n=1, shape=10,scale=2)[1] 0.2608497
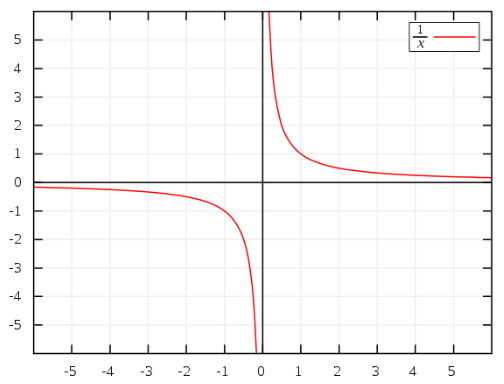
invser gamma分布就是gamma分布的倒数(reciprocal)。更准确的说如果x服从gamma(a,b),则y=1/x服从inverse-gamma(a,1/b)。其实知道它们的关系是很重要的,因为有的时候用的不是方差,而是precision(方差的倒数)作为分布的参数。
什么是reciprocal
gamma分布的应用
gamma/inverse-gamma分布在Bayesian Inference中使用比较广泛。无论是empirical Bayes还是基于MCMC采样的后验分布计算,它主要作为非负实数的先验分布(比如方差)出现。在empricial Bayesian的计算中,gamma分布是正态似然函数的共轭先验,因此有关的后验分布可以不做MCMC,直接根据公式计算。

例如在方差未知的条件下,我们假设方差来自gamma分布。
下面的例子是方差和均值都未知的情况,假设总体的均值来自于Norm(μ0, σ0^2),总体的方差来自于gamma(α, β)。
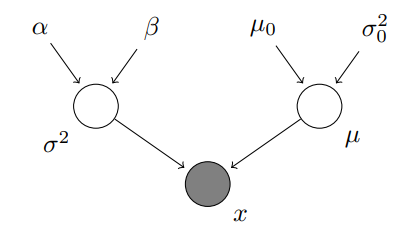
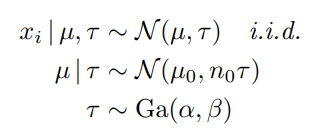
后验分布为:
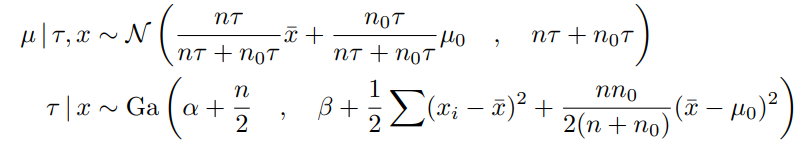
当然很多情况下是无法产生像上面一样的解,因此需要做MCMC采样,gamma/inverse-gamma分布也经常作为未知参数(比如,方差)的先验分布。
(附赠一份先验选择速查表)
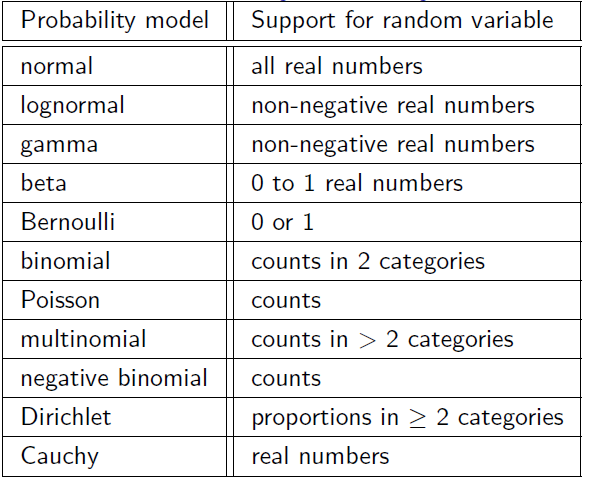
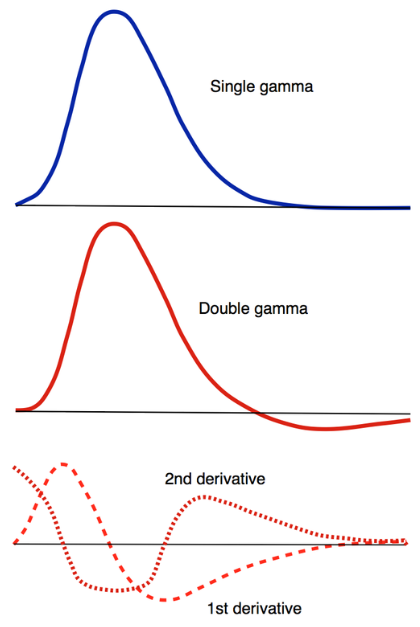
btw, SPM默认的HRF就是用两个gamma函数生成的
见spm_hrf.m和spm_Gpdf.m
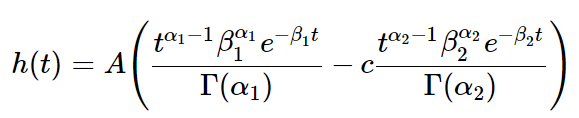

Recap:
gamma分布的参数及作用
dgamma/qgamma/pgamma/rgamma函数的用法
gamma分布的应用







