论文名称:A Unified Framework for Marketing Budget Allocation
本文试图解决的问题是:营销预算应该如何在不同子市场之间进行分配,以达到销量最大化的目标。在计算广告中,也会涉及到如何将广告主的预算分配在不同的子流量上(如搜索、推荐等),以达到ROI最高(或其它指标)的目标,具有一定的参考意义
1.摘要
营销预算分配在传统商业中已经有十几年的研究历史,而在电子商务中,由于环境的动态性和决策过程的复杂性给营销预算分配的研究带来了诸多挑战。本文提出了一个新的营销预算分配统一框架。基于丰富的数据资源,使用数据驱动的方法可以帮助我们克服挑战,并作出更智能的决策。在该方法中,我们建立了一个半黑盒模型来预估动态市场的反馈,并提出了一种有效的方法来解决复杂的分配任务。通过半黑盒模型探索历史数据,预测各个细分市场的反馈,其中,我们通过神经网络扩展了logit需求曲线的能力。反馈模型能够给出销量和营销成本之间的关系,在反馈模型的基础上,预算分配被表述为一个优化问题。在一个统一的优化范式中支持多种业务约束,包括成本上界、利润下界或ROI下界。该框架易于实现,且适合处理大规模问题。它已经成功应用于阿里巴巴集团的多个场景,离线实验和在线A/B实验均证明了该方法的有效性
2.介绍
你应该在什么时候和在什么地方花钱?这个问题的答案是营销预算分配的关键,它在传统商业中已经研究了几十年。相比传统商务环境,电子商务的环境和决策过程更加动态和复杂。电子商务环境中,营销预算分配是比较复杂的,需要经常调整,比如每周甚至每天,而传统商务的营销预算分配一般每年只需要调整几次。这给拥有大型和多样化市场的公司带来了巨大的挑战。幸运的是,在电子商务环境中,商业活动可以通过从多个来源收集的数据来跟踪和描述。通过利用这些数据,数据驱动的方法可以帮助我们克服上述挑战。智能技术可以让我们对市场有更透彻的了解,并作出更明智的决策。此外,当市场处于被自动监控和分析的状态时,可以更快地发现新的市场趋势,从而及时调整预算分配。在本文中,我们提出了一个新的营销预算分配统一框架,它包含两个循序渐进的步骤:1)从历史数据中学习市场反馈的模型;2)在反馈学习模型的基础上优化预算分配。整个框架如图1所示:
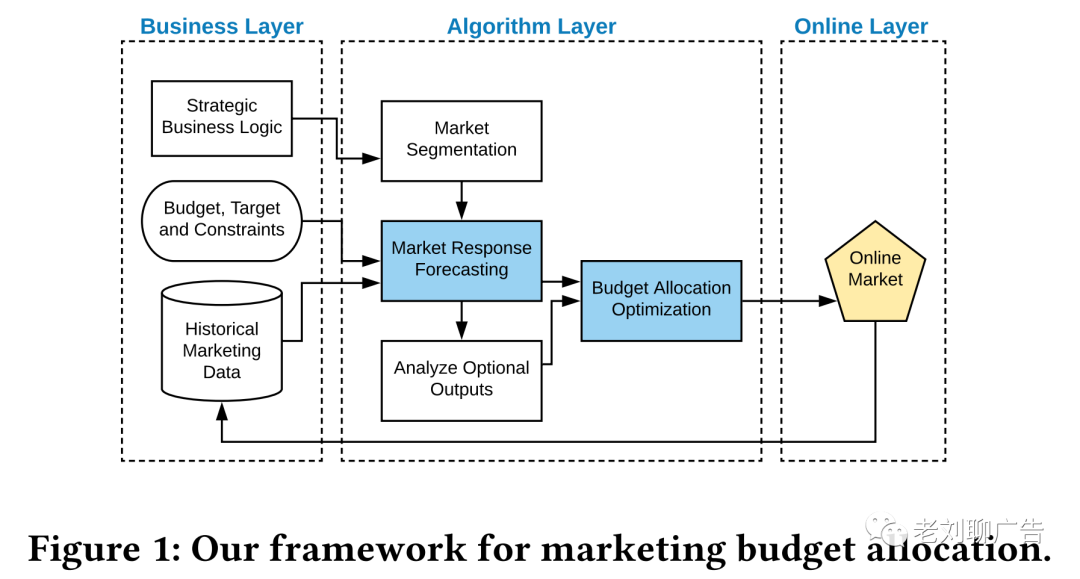
在市场营销中,整个市场根据商品种类、顾客种类、消费时间等细分为许多不同的细分市场。为了解决如何将预算分配到每个细分市场,我们需要预测这么一个事情:给定预算划分到每个细分市场的分配方案,每个细分市场的销量反馈。虽然神经网络等黑盒预测方法在许多应用中得到了广泛的应用,但在预测和决策之间仍存在一些差距。最大的挑战之一是如何将黑盒预测转化为分配决策。相比之下,经济学中非常流行的logit需求曲线有着明确的表达方式。然而,如果单独拟合每个细分市场的logit曲线的话,不同细分市场之间的信息就不能实现共享,这可能会导致严重的数据稀疏问题。因此,我们提出了一种半黑盒模型,借助神经网络来扩展logit需求曲线的能力。预测的输入首先分为两个不同的部分:独立变量和上下文变量。独立变量是指分配给每个细分市场的预算,上下文变量是指细分市场的内在属性,如商品品牌、消费者居住城市、消费时间等。结果表明,logit反馈模型的市场平均成本(或市场成本)弹性是由偏差参数决定的。我们以上下文变量为输入,使用同一个神经网络计算所有细分市场的偏差参数。在此基础上,将对logit需求曲线的拟合扩展为对市场成本弹性的学习过程,并给出每个细分市场的特定敏感性系数,明确地描述了销量与成本的关系
只要得到反馈模型,预算分配就可以表述为一个最优化问题。用表示细分市场的数量,在一定的预算约束下,预算分配需要对个变量进行优化才能使得销量最大化。由于需求曲线的非凸性,优化问题也是非凸性的,我们将问题重新表述为一个等价的凸优化问题。通过引入对偶变量,应用拉格朗日乘子法,根据KKT条件,将原问题简化为对偶变量的寻根问题,只需对一个对偶变量进行二分求解,而无需搜索个原变量。该算法在几轮迭代中就会收敛,每次迭代的时间复杂度是,因此,适合处理大规模问题。类如成本上界、利润下界或者ROI下界,都可以在一个统一的优化框架中得到支持,只需要进行少量调整即可。更重要的是,优化框架可以很容易地扩展到离散场景,预算变量只能从一组离散值中获取。之所有考虑离散决策变量,主要是因为在许多折扣或者高价的场景下,存在大量以99、199等结尾的价格。我们将证明离散场景下的问题可以由松弛连续问题的解构造一个多选择背包问题(MCKP)来求解。该框架易于实现,且已经成功在阿里巴巴多个业务场景下得到应用,如淘票票、双十一购物节等
3.市场反馈
3.1 logit反馈模型
营销预算分配的基础组成部分是当预算花在某个细分市场上时,这个细分市场的销量反馈。神经网络作为一种黑盒预算方法,具有强大的功能和广泛的应用场景。然而,将黑盒预算转化为分配决策还存在许多挑战。相比之下,经济学中的需求曲线通常有明确的表达式。需求曲线有很多种,如线性、对数线性、常弹性、logit等,我们主要关注logit需求曲线
第个细分市场的logit模型定义如下:
图2给出了一个简单的例子:
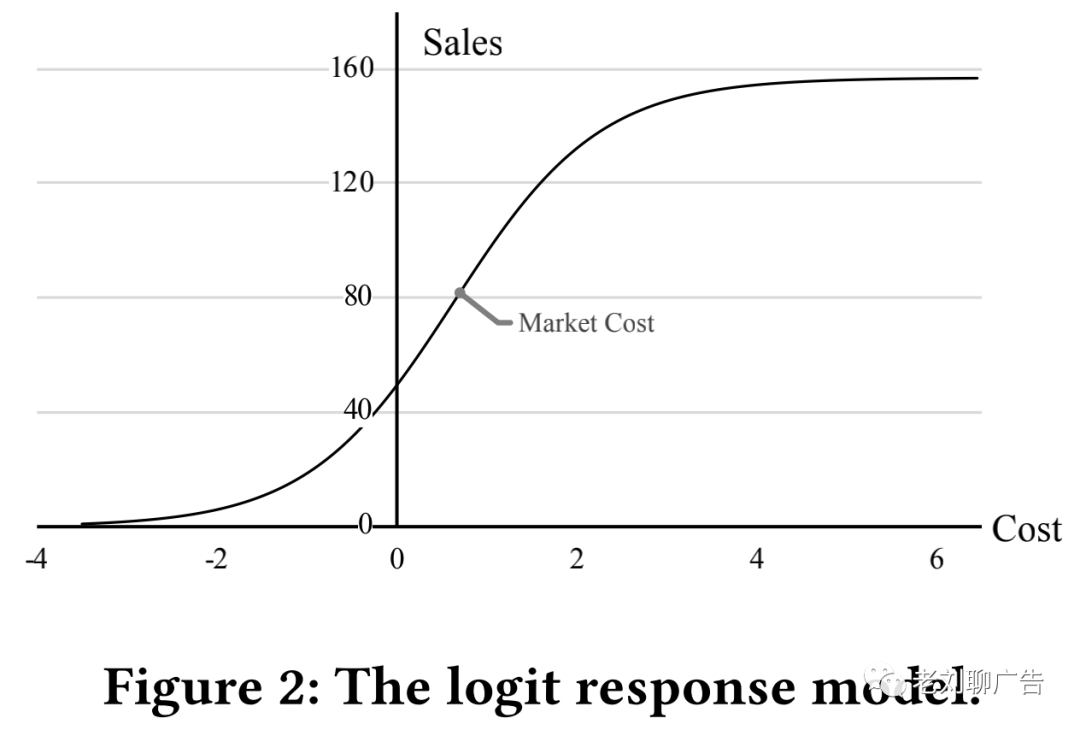
其中是单位营销成本,是第个细分市场的整体规模。可以大于0,也可以小于0。大于0的成本表示正在进行价格促销,小于0的成本表示价格溢价。第个细分市场的整体规模可以提前使用统计方法获取。因此,需要学习的参数是。表示正常情况下的灵敏度,这意味着更大的营销成本可以带来更高的销量。在图2中,反馈曲线在点处非常陡峭,这个点我们称作market cost,它表示第个细分市场的平均营销成本。当营销成本在点附近时,销量和营销成本的关系是非常敏感的。换句话说,即使成本的变化很小,销量也会有很大的变化。当成本远离市场平均成本时,它们之间的关系就不那么敏感了,这被称为边际效应递减
最常用的敏感度测量方法是弹性。受价格弹性的启发,我们将成本弹性定义为销量的百分比变化与成本的百分比变化的比值:
因此,点处的弹性可以通过对公式(2)求极限获得:
THEOREM 1:logit模型在市场成本的弹性是
3.2 半黑盒模型
模型利用数据的能力是有限的,更具体地说,当我们在学习参数和时,模型没有办法共享不同细分市场之间的信息。对于那些历史上预算分配值不同次数比较少的细分市场,可能会导致严重的数据稀疏问题。实际上,预测模型的输入变量可以分为独立变量和上下文变量两种。独立变量就是分配给每个细分市场的预算,用表示,上下文变量是市场的内在属性,用表示,其中可能包括商品品牌、商品类别、消费者居住城市、消费时间等。虽然上下文变量在不同的细分市场有所不同,但它们不会随着每个细分市场的独立变量变化而变化。传统的神经网络将和同时作为输入,并以黑盒的方式将它们与销量联系起来。与之相反的是,模型的输入只有,并把它与销量以明确的方式联系起来。我们提出了一个半黑盒模型,它以和为输入,并以明确的方式保持和销量之间的关系
假设一:logit反馈模型的市场成本弹性取决于上下文变量
直观上这个假设是合理的。例如,T-shirts在夏天的弹性要比冬天低很多,电影票在周末的弹性要比工作日低很多。与直接预测最终销量不同的是,我们使用一个神经网络来预估市场成本弹性,即每个细分市场的。基于,不同市场之间的弹性信息可以实现共享。因此,传统的模型被扩展为一个半黑盒模型:
该方法结合了神经网络的预测能力和需求曲线的表达能力
神经网络的参数和需要学习获得。我们首先定义市场份额如下:
其中,,可以提前使用简单的统计方法获得,因此,可以很容易地在每个细分市场上构建训练集,然后可以通过梯度下降来最小化下面的负对数似然函数来学习参数:
4.预算分配
只要得到反馈模型,预算分配就可以表述为一个优化问题
4.1 问题定义
假设有个细分市场,预算分配需要在一定预算约束下对每个细分市场分配预算。定义,我们的目标是在预算约束下找到最优的来最大化整体销量。因此,该问题可表述如下:
其中,是我们的预算约束,它可以是正数,也可以是负数。正数代表成本上界,负数代表利润下界
因为是关于的非凸优化问题,直接解决这个问题是非常困难的。我们可以重新将这个问题表述为一个等价的凸优化问题。当时,是一个明显的单调增函数,我们可以得到它的反函数,将市场份额映射到营销成本,如下:
我们定义以及约束函数如下:
THEOREM 2:g(q)是关于q的凸函数
因此,我们可重新定义原问题如下:
它是关于的凸优化问题
4.2 算法
通过引入对偶变量,利用拉格朗日乘子法求解凸优化问题(10):
KKT条件。目标函数和约束函数都是可微的,而且是凸的,KKT条件是:
其中,分别是原问题和对偶问题的最优解,且对偶间隙是0
由于是凸函数,它的最小值是存在的,用表示它的最小值。为了获得最小值,我们对求偏导并使其等于0。可以得到:
可以通过Lambert W函数获得:
其中是Lambert W函数。如果,该问题无解;如果,可以直接得到最优解;如果,则下面的假设成立:
ASSUMPTION 2:存在,使得成立
当上述假设成立时,约束条件满足Slater条件,等式(12)中的KKT条件为最优性提供了充要条件
THEOREM 3:第4个KKT条件等价于:
我们可以看到最优解可以用对偶变量来表示。这就是说,搜索个最优变量等价于搜索一个对偶变量。重新定义如下:
以及:
如果只有一个解,那么问题的最优解就是
决策方法。二分法是一种数值求解方法,该方法反复将两个值定义的间隔一分为二,当间隔足够小时中断
THEOREM 4. 函数是关于严格单调递减的,且

当假设2成立时,存在使得。结合THEOREM 4,使用二分法可以求得的解,如算法1所示。从上面可以看到,为了满足约束,我们设置。在实践中,当或者时,搜索将会被中断
时间复杂度:如算法1的第2~4行描述,找到满足的至多需要次迭代。如第5~12行描述,找到满足要求的解至多需要。因此,总的迭代次数小于。如果算法被条件提前中断,迭代次数至多为。因此,总的迭代次数是小于一个常数的,如。实践中只需要少量迭代即可收敛,每次迭代的时间复杂度为O(N),因此适合处理大规模数据问题
4.3 扩展
在很多情况下,很难去确定一个具体的总预算值,可以限定预算支出和收入的比值不低于某个值,用表示的下界,方程(7)表示的原始问题可表述如下:
约束函数(9)可以重写如下:
THEOREM 5:是关于的凸函数,是关于的单调递减函数,且
经过简单推导可知,新的优化问题仍旧能够使用算法1来解决。等式(16)中的计算方式可以用下式替代:
预算不再是必需的
附录
THEOREM 1证明:
对等式(1)求导可得:
将上市代入式(3)可得:
将代入即可
THEOREM 2证明:
对函数g求二次导,证明其大于等于0.即可证明其是凸函数






