2020年参加了MothorCup建模竞赛选择了C题承运人平台定价问题,其中第三问尝试了非常有挑战性的ELM算法,一直想把找个机会总结一下这个模型。
摘要
针对问题三,首先,选取附件 1 中已成交的历史交易数据,并选取问题 1 中分析出的三种调价形式下影响其定价的主要因素,作为其自变量,线路价格作为因变量;选取影响三种调价形式的公共因素,作为计算线路总成本的自变量,线路总成本作为因变量, 构建四个基于极限学习机智能优化算法的线路定价回归模型,训练模型,直至训练一个成熟模型。其次,可以对附件 2 中的新的数据集进行预测,得出三次报价和线路总成本。通过计算预测精度以及误差等测度,分析评价得出的结果,并给出合理的调价策略。
一:问题重述
1.1问题背景:
无车承运人平台需解决承运线路的科学定价问题,以保证围绕货主、无车承运人平台以及承运人为主体的运营模式得以合理高效。研究从无车承运人视角出发,仅考虑面向承运人的线路运输任务提出动态定价具有重要意义。本文通过建立数学模型,提出具有针对性解决策略,解决无车承运平台通过合理定价、调价,以较低的承运成本,较短的交易时间,高效促成货主与承运人双边市场的成交问题。
1.2:问题分析
问题 3 要求建立线路定价数学模型,解决定量计算附件 2 中新的交易任务的三次报价及总成本定价,并且计算出的结果将用于测试报价的准确性,对某个任务,若三次报价中又一次成交,则后续价格将不再考虑。这就要求三次报价需要全部给出,无论该任务属于何种调价形式。同时给出调价策略以及评价本问题中计算出的所有定价。此类问题属于一种回归预测类型的问题,可以通过附件 1 中已成交的历史交易数据,并选取问题 1 中分析出的三种调价形式下影响其定价的主要因素,作为其属性,定价作为标签,构建四个回归模型,进行训练,直至训练一个成熟模型,然后可以对附件 2 中的新的数据集进行预测,通过计算预测精度以及误差等测度,分析评价得出的结果,并给出合理的调价策略。
二:模型假设
1、假设数据中所发布线路任务全部为固定车型的整车任务,即任务与某种车型一一对应,不考虑拼载任务。
2、假设在外部环境对无车承运平台的影响是复杂的,主要体现在服务需求量的变化中。
3、假设无车承运平台与达成的运价报价一定时期内不变,模型中的定价为无车承运平台的报价。
三、符号说明
符号 | 解释说明 |
W1 | 主成分分析权重 |
W2 | 灰色关联度分析权重 |
W | 两种方法组合权重 |
rij | 相关系数 |
akj |
标准化后指标 |
ai | 表示主成分 Fj 的信息贡献率 |
四、模型的建立与求解
通过问题 1 对三种形式的调价情况的分析,首先,对每种调价形式的定价与其影响因素之间的关系,分别选取前 6 个、前 5 个、前 4 个指标为三种调价的影响因子。基于考虑总成本定价与不同调价形式下的定价都存在着某种内部联系,故选取三种调价形式的公共影响指标作为其影响因子。其次,建立基于 Extreme Learning Machine (ELM)的线路定价回归数学模型,分别将上述三次调价形式与总成本定价的影响因子作为输入向量,训练模型,并对附件 2 中新给出的所有线路任务交易数据的报价进行回归预测,最终确定所有线路任务的三次报价及总成本定价。
(1)平台处于初步发展过程中时,进行首次报价是以实际承运商司机和货主为主要影响因素进行定价。其依赖这两个双边市场的规模,其规模越大,无车承运平台对双边用户的定价会相对较低。此外,双边市场用户对无车承运平台的体验满意度越高,其对双边市场用户定价越高。无车承运平台的服务成本和需求弹性越大,对双边用户的定价越高。
(2)对于面临相对较为稳定的竞争环境下,无车承运平台定价时,需要考虑不同平台采取不同的定价结构。如对优势平台,需采取对货主收取较高价格,对实际承运商收取较低价格的倾斜定价。
(3)对于面临激烈竞争环境下,无车承运平台定价,需要考虑两阶段的利益,为获得竞争优势,需要在第一阶段对货主和实际承运商定价较低,考虑第二极端的利益,需要采取对货主收取较低价格,对实际承运平台提高定价的倾斜定价策略。
对计算出的三次报价和线路总成本进行评价时,采用问题 2 中的方法,首先将所有数据的三次报价和线路总成本作为 4 个评价指标,其次,采用基于 K-means 无监督聚类算法,将数据集聚类成 4 个簇,分别代表优、良、中、差 4 个等级的样本簇。根据实验测试,我们利用 K-Means 将表中的数据分为 4 类,由于 4 个评价指标的量纲都一致,所以无需对数据进行标准化处理,直接可以做聚类
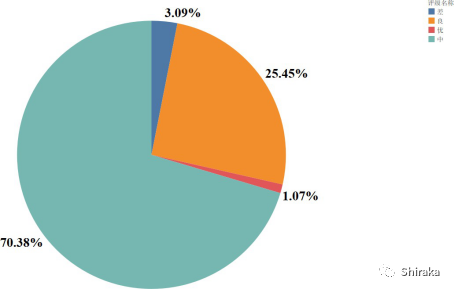
图 4-11 各评价等级百分比图
通过聚类类别情况结果,统计每个簇的频数及百分比并整理每个簇的样本数据,并且将统计的方差分析差异对比结果最优进行加粗标注,以便后续进行分析。
cluster_1(n=38) | cluster_2(n=1427) | cluster_3(n=14) | cluster_4(n=10) | |
总里程 | 2544.00±0.00 | 96.72±76.62 | 2548.06±15.20 | 2569.17±23.36 |
需求类型 2 | -1.00±0.00 | -0.74±0.67 | 1.00±0.00 | -0.60±0.84 |
车辆长度 | 15.00±0.00 | 6.67±2.31 | 15.00±0.00 | 15.00±0.00 |
车辆吨位 | 30.00±0.00 | 6.80±5.50 | 30.00±0.00 | 30.00±0.00 |
标的展示策略 | 1.00±0.00 | 0.47±0.88 | 0.29±0.99 | 0.60±0.84 |
需求紧急程度 | 0.31±0.05 | 0.37±0.19 | 0.39±0.14 | 0.90±0.00 |
根据聚类类别方差分析差异对比结果,样本中有 70.38%是“中”,有 25.45%是“良” 差和优相对最少,只含有 3.09%、1.07%。承运商成交的价格,数值越低,说明承运人平台以较低的成交价格促成交易,达到效益最大化,并在相对较少的调价时间内,同时也节省了时间开销。此外,此结果也说明了本次计算的三次报价和最终成交价格大部分是较为正常的数据,属于中等级别以上,可供平台定价参考。
五、模型评价与改进
本文模型在计算未知交易任务的定价过程中,分别对不同调价形式进行基于ELM 的回归预测,充分利用 ELM 智能算法的良好泛化性能与较低的时间复杂度,只需调节其中的隐层神经元的个数,易于实现给定规模的样本数据,并且模型预测效果较好,误差较低,有良好的实用价值。
本文模型均是通过给定历史交易数据,从中挖掘有用信息,但是在实际情况中,平台定价还会涉及到其他各类因素,在此模型中忽略实际运输作业的货物集散、装卸后续流程,比较有局限性。
本文模型均忽略货主参与实际承运过程中的议价博弈过程,模型考虑情况较为理想化,还有待完善。
5.2模型的推广
继续深入挖掘平台历史交易数据的潜在价值,对有价值的数据采取量化建模,有力实现对平台定价的评价与预测。
由于智能算法在模型训练时往往对参数依赖性较强,对任何数据集,探索性采取一定方法进行参数寻优,以达到提高模型训练速度与泛化性能。






