提到KNN(K-Nearest Neighbors),大家的第一印象大概是它是比较简单且易于实现的有监督算法,既可以解决分类问题,也能解决回归问题。
尽管KNN已不是时代的主流,但深入了解它的基本原理还是有必要的。大家可以通过下面几个问题来看看自己对KNN的理解情况:
1. KNN基本原理是什么?
2. 如何确定k?
3. 如何选择距离度量方法?不同距离度量方法对数据集有哪些要求?
4. KNN如何实现距离加权?
5. 多数类投票的优化目标等价是什么?
6. 均值回归的优化目标是什么?
7. 什么是KD树,为什么KD树能加快KNN的检索效率?
8. KD树如何构造?
9. KD树如何检索?
如果以上问题你都能轻松回答,那本文后续的内容可以帮助你加强知识记忆。如果对上述问题有疑惑,那本文后续内容将会帮助你进一步加深对KNN的理解。
在看算法具体细节之前,我个人建议是先了解下它是怎么来的。本文先简单介绍KNN的历史,然后介绍算法的基本原理,之后针对如何加快KNN的检索效率,介绍KD树相关内容。
一、KNN简史
1951年,Evelyn Fix和Joseph Lawson Hodges Jr. 最早提出了最近邻规则。但由于当时社会环境问题,他们并未发表这方面的工作。
1962年,George S Sebestyen在《Decision-making processes in pattern recognition》中将KNN称作邻近算法(Proximity Algorithm)。
1965年,Nils J. Nilsson在《Learning Machines: Foundations of Trainable Pattern-Classifying Systems》中将KNN称作最小距离分类器(Minimum Distance Classifier)。
1967年,Thomas Cover和Peter Hart在论文《Nearest neighbor pattern classification》中正式介绍了KNN,这也是KNN的首次正式发表。
在KNN提出之后,后续的研究工作主要集中在两个方面:效率和效果
效率优化:KNN比较适用于样本量较大的问题,样本量较小的问题采用KNN比较容易产生误判。因此,事先对样本特征进行约减,删除对分类结果影响较小的属性,便成了KNN效率优化的一个主要方向。2006年,Zhang等人在论文《SVM-KNN: Discriminative nearest neighbor classification for visual category recognition》中提出基于SVM和KNN在相似性度量框架中考虑视觉类别识别。在2007年,Zhang等人在论文《ML-KNN: A lazy learning approach to multi-label learning》中针对有限的数据设计了针对多标签数据的KNN算法。2009年,Chen等人在论文《Fast Approximate kNN Graph Construction for High Dimensional Data via Recursive Lanczos Bisection》中利用两种divide and conquer方法来近似KNN的计算。
效果优化:效果优化的核心目标是提升KNN的分类精度。1986年,Stanfill和Walt在《Toward memory-based reasoning》中采用价值距离指标(Value Distance Metric/VDM)。Han等人于1999年在《text categorization using weight adjusted k-nearest neighbour classification》中针对文件分类实做可调整权重的k最近邻居法WAkNN (weighted adjusted k nearest neighbor),以提升KNN的分类效果。2004年,Li等人认为不同分类的文件本身有数量上有差异,因此应该按照训练集合中各种分类的文件数量,对KNN选取不同的k。2004年,Goldberger等人在《Neighbourhood components analysis》(NCA)中将马氏距离应用于KNN中,实现降维的效果。NCA主要目的是通过找到一个线性变化矩阵,来最大化leave-one-out (LOO)分类精确度。
以上是对KNN发展的简介,从最开始的思想萌发,到后续的效率和效果的不断优化,研究人员们持续了近60多年的探索。值得一提的是:虽然KNN已经渐渐淡出大众视野,但它仍然是大多数领域首选Baseline。
二、算法介绍
下面我们开始进入KNN算法的具体细节。
1、算法原理
KNN是一种分类、回归算法,既可用于解决分类问题,又可用于解决回归问题,其核心思想可以概括如下:
分类问题:对于样本,根据其个距离最近的训练样本的类别,采用多数类投票方式来预测的类别 回归问题:对于样本,根据其个距离最近的训练样本标签的均值作为的预测结果
KNN的核心三要素如下:
的选取 距离度量 决策规则
与传统机器学习算法不同,KNN属于lazy learning
算法,它不具有显式学习的过程(即不需要对模型进行训练),对于待预测样本,直接根据训练集进行预测。
lazy learning
:开始时算法将训练样本储存好,并不会根据训练样本来优化模型。到预测阶段,算法才会分析待预测样本与训练样本之间的关系,来判定待预测样本的预测值结果eager learning
:在训练阶段,算法先利用训练数据训练一个预测模型。到预测阶段,算法会利用预测模型对待预测样本进行打分
此外,KNN属于非参数学习算法(是超参数,无需训练)。由于KNN具有非常高的容量(Capacity),它在具有较大数据集上能达到较高的精度。
但,KNN具有如下三个比较明显的缺点:
传统KNN的计算成本高,时间复杂度为 训练集较小时,泛化能力很差,容易过拟合 没法判断特征重要性
2、k的选取
对于不同数据集,值没有一个通用的确定方法。但在实际应用中,一般选择一组比较小的值(如,3、5、7、9等),再采用交叉验证法来最终确定最优的。
需要说明的是:的大小会直接决定了模型的复杂度:
值较小时,对应模型的复杂度较高,相当于利用较小邻域的训练样本进行预测,学习的偏差较小;由于只有邻域内的训练样本会对预测结果起作用,预测结果会对近邻的样本点非常敏感,这样导致学习方差较大。因此,减小值意味着模型变复杂,也就易发生过拟合
值较大时,对应模型的复杂度较低,相当于利用较大邻域的训练样本进行预测,学习方差较小;但由于较远的训练样本也会对预测结果起作用,学习偏差较大
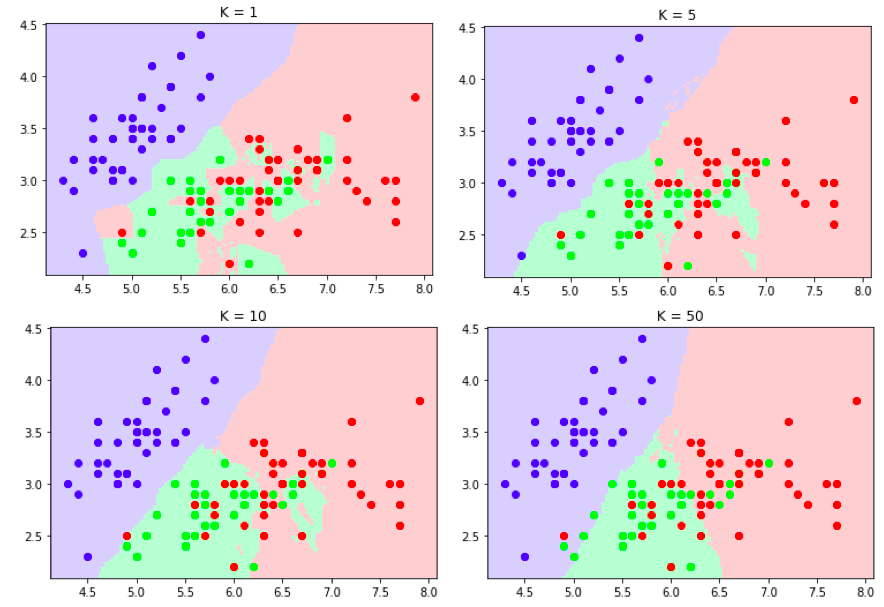
决定了模型的复杂度,当数据集较复杂、数据量较多时可以选择较小的,反之如果数据相对简单、数据量较小,可以选择相对较大的。
3、距离度量
KNN另一个核心问题是如何在特征空间中确定近邻样本,即如何度量样本间的距离。
关于距离度量大家可以参考我之前的一篇公众号文章《19种距离度量方法》,里面总结了常用的19种距离度量方法。
不同的距离度量所确定的最近邻点是不同的,这里只简单介绍下距离:
其中,为维特征空间的两个样本点
当时,表示欧氏距离 当时,表示曼哈顿距离 当是,表示切比雪夫距离(各维度差异的最大值)
4、预测规则
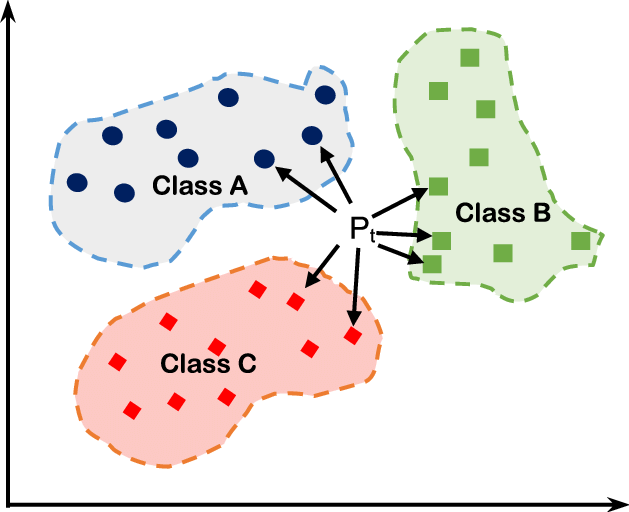
A) 分类决策
KNN在做分类时,通常采用多数类投票;也可以根据距离远近加权:距离越近则样本的权重越大。
多数类投票:
其中,表示的第个近邻样本的label。最终决策为:
距离加权:
距离加权投票的决策为
其中,权重可以根据样本与训练近邻样本的距离决定,距离越近权重越大,越远则权重越小:如
可以通过数学证明:多数类投票方法等价于经验风险最小化(感兴趣的可以自己证明一下)
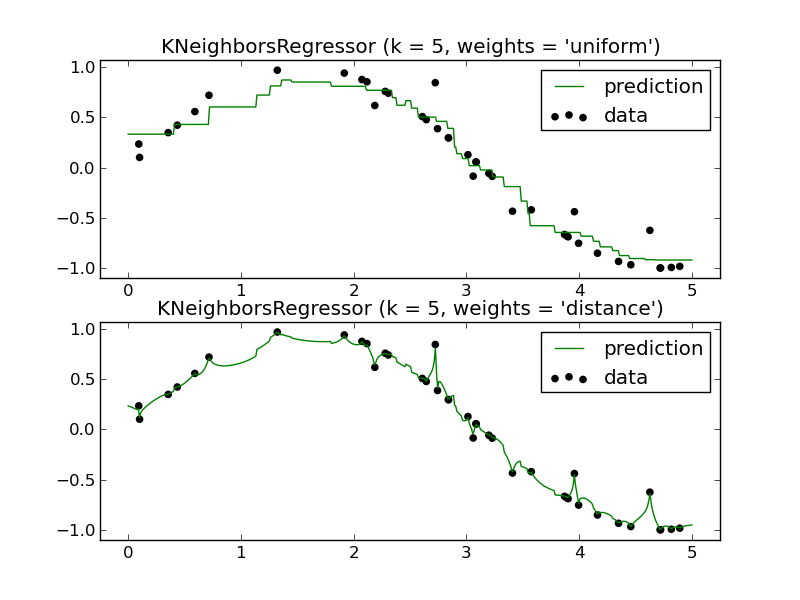
B) 回归决策
采用KNN做回归任务时,通常采用均值回归;也可以根据距离远近加权:距离越近则样本的权重越大。
均值回归:
其中,表示的第个近邻样本的标签值。
距离加权:
同样可以通过数学证明:均值回归等价于经验风险最小化(感兴趣的可以自己证明一下)
三、KD树(K-Dimensional Tree)
KNN在应用中的一个核心问题是:如何在训练数据中快速进行邻搜索。
最简单的办法是直接进行线性扫描
:针对输入样本,计算其与每个训练样本的距离,最终得到最近的个训练样本。但这种方法耗时高(时间复杂度)、效率低,当训练集较大时,无法满足应用需求。
KD树是一种高维数据的快速查询结构(二叉树),能对k维空间的样本点进行存储和快速检索。因此,通常采用KD树来实现对近邻样本的快速检索,使KNN的查询时间复杂度降至。下面我们具体了解下KD树算法。
1、KD树构造
KD树的构建算法如下:

对应python
代码如下:
def kd_tree_build(points, dim, l=0):
if len(points) > 1:
points.sort(key=lambda x: x[l])
l = (l + 1) % dim # py中维度下标是从0开始的
half = len(points) >> 1
return [
kd_tree_build(points[:half], dim, l), # left
kd_tree_build(points[half+1:], dim, l), # right
points[half] # current_node
]
elif len(points) == 1:
return [None, None, points[0]]
KD数的构造过程如下:

图片来源:Hierarchical data representation structures for interactive image information mining
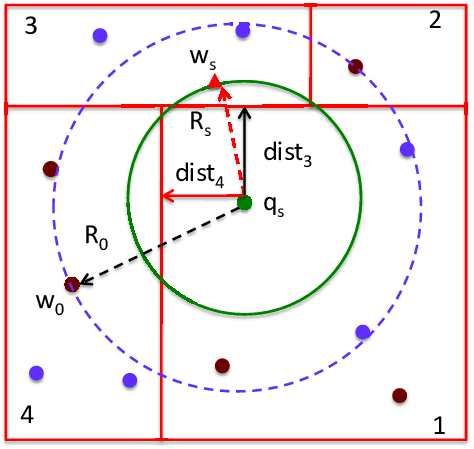
2、KD树搜索
KD树的查询算法如下:

对应python
代码如下:
def kd_tree_search(node, point, k, dim, dist_func, l=0, heap=None):
is_root = not heap
if is_root:
heap = []
if node is not None:
dist = dist_func(point, node[2])
diff = node[2][l] - point[l]
if len(heap) < k:
heapq.heappush(heap, (-dist, node[2]))
elif dist < -heap[0][0]:
heapq.heappushpop(heap, (-dist, node[2]))
l = (l + 1) % dim
for b in [diff < 0] + [diff >= 0] * (diff * diff < -heap[0][0]):
kd_tree_search(node[b], point, k, dim, dist_func, l, heap)
if is_root:
neighbors = sorted((-h[0], h[1]) for h in heap)
return neighbors
其中dist_func
是距离度量函数,如下面的欧氏距离,更多距离度量方法可以参考之前的公众号文章:《19种距离度量方法》
import numpy as np
def euclidean_dist(x, y):
n_x = np.array(x)
n_y = np.array(y)
return np.sqrt(np.sum(np.square(n_x - n_y)))
参考文献
[1] E. Fix and J.L. Hodges. An Important Contribution to Nonparametric Discriminant Analysis and Density Estimation. 1951
[2] Who invented the nearest neighbor rule? http://37steps.com/4370/nn-rule-invention/
[3] George S Sebestyen. Decision-making processes in pattern recognition. 1962
[4] Nils J. Nilsson. Learning Machines: Foundations of Trainable Pattern-Classifying Systems. 1965
[5] C. Stanfill and D. Waltz. Toward memory-based reasoning. Communications of the ACM, vol. 29, pp. 1213-1228, 1986.
[6] https://github.com/Vectorized/Python-KD-Tree






