“ 上篇主要讲述了各种检验方法及适用条件,我回去细看了一下,感觉可能写得不够全面,很多都是我理所当然觉得大家能理解的,对小白可能还是不够友好,所以适当做下补充。”
01
—
什么是假设检验
A、先对总体的参数(或分布形式)提出某种假设,然后利用样本信息判断假设是否成立的统计方法。
B、有参数检验和非参数检验。
C、逻辑上运用反证法,统计上依据小概率原理,两者强强联合。
02
—
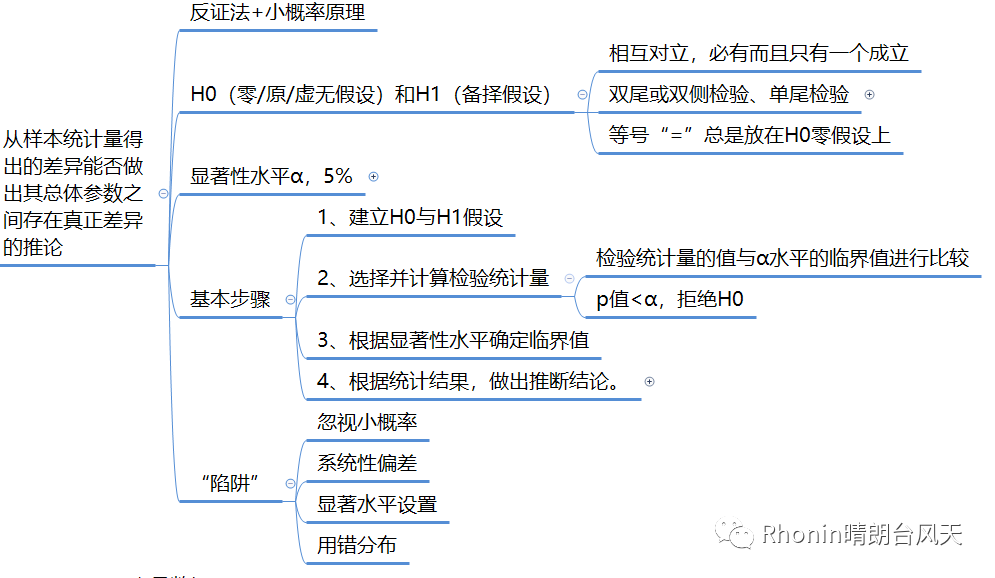
H0(零/原/虚无假设)和H1(备择假设)
A、H0与H1是一个完备事件组,两者相互对立,必有而且只有一个成立。
B、一般H1代表我们真实意愿,H0是对立意愿,我们通过证明H0结论发生的概率特别特别小,这样就可以推翻H0结论,接受和它相反的H1结论。
先确定H1(备择假设),再确定H0(零假设)。
C、如果假设是没有特定方向性,并含有“=”或“≠”符号的假设检验称为双尾或双侧检验。
如果假设是有特定方向性,并含有“>”、“<”、“>=”、“<=”符号的假设检验称为单尾检验。
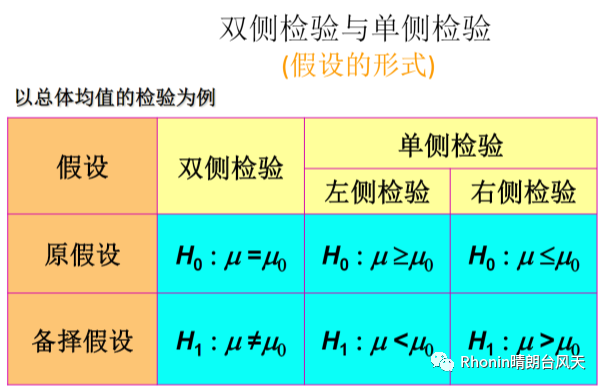
D、等号“=”总是放在H0零假设上。
03
—
两类错误与显著性水平
我们的推断决策是建立在样本信息基础上,但是样本是随机的,那么就有可能犯错误。有分以下两类错误:
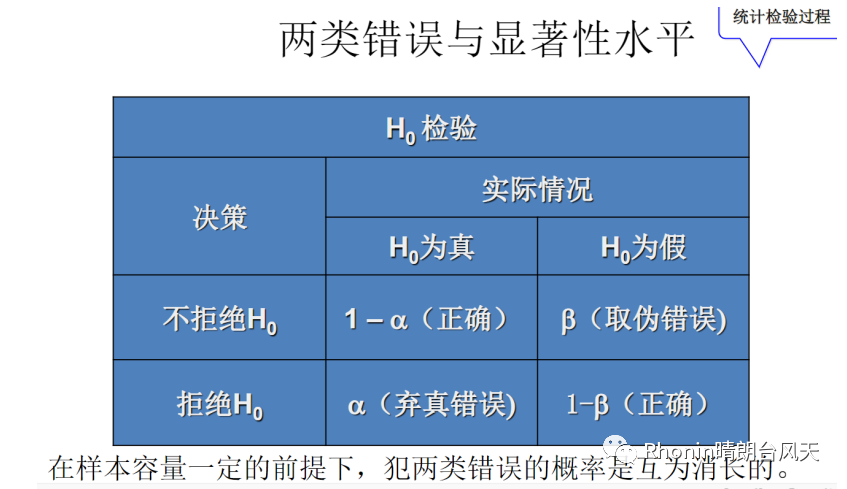
一般来说要看哪类错误的代价成本会高些,就控制哪类错误发生的概率,第Ⅰ类错误会先被控制。
其实别太纠结这个,我们重点放在α这个显著性水平上。
常用的α值有:1%,5%,10%。选择哪个标准要看情况,通常都是5%。
04
—
假设检验基本步骤
A、基本步骤:
1、建立H0与H1假设
2、选择并计算检验统计量
3、根据显著性水平确定临界值
4、根据统计结果,做出推断结论。
B、检验统计量
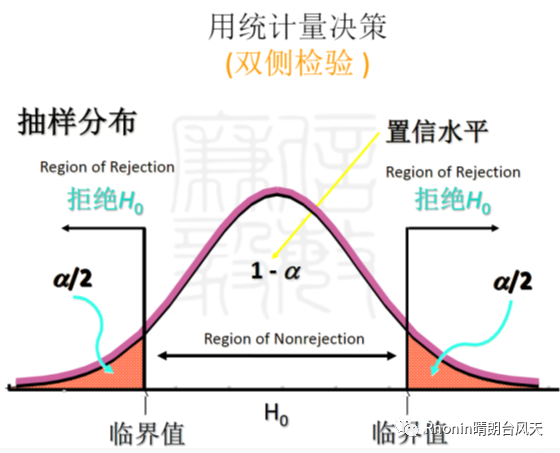

C、判断关键:检验值和P值
检验值决策规则:
1、给定显著性水平α,查表得出相应的临界值,比如Zα或Zα/2。
2、将检验统计量的值与α水平的临界值进行比较。
3、做出决策
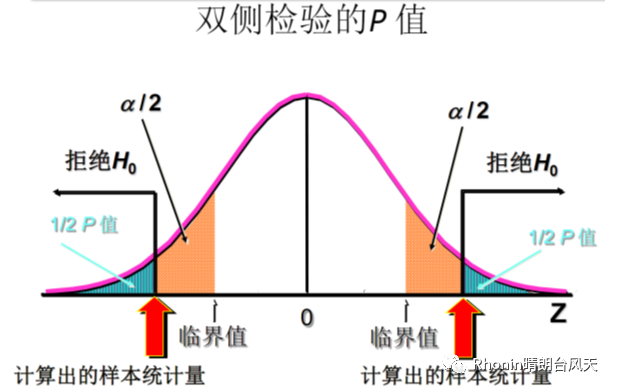
双侧检验:|统计量|>临界值,拒绝H0
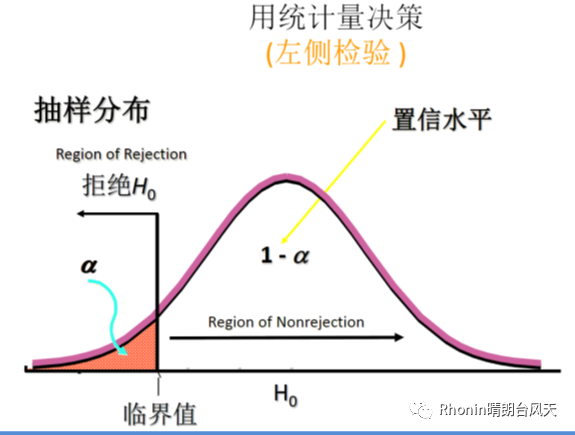
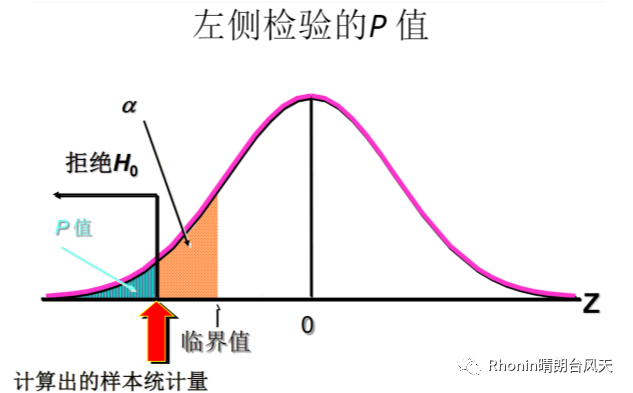
左侧检验:统计量<-临界值,拒绝H0
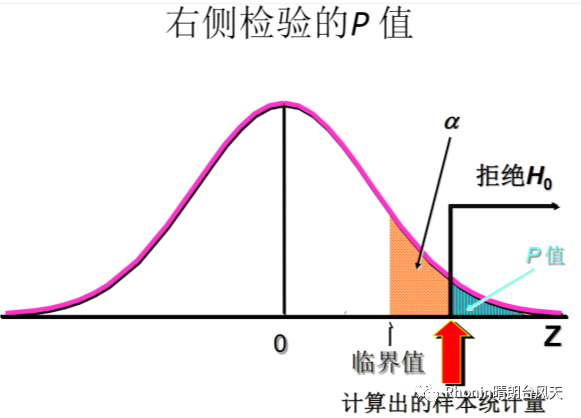
右侧检验:统计量>临界值,拒绝H0
P值,样本的概率,决策规则:p值<α,拒绝H0
我个人会更倾向于用这个,方便直观,反正一看p值<0.05就可以拒绝了。
D、推断结论参考:
“单样本t检验(写明采用的检验方法)结果显示,XX(样本数量)验证对象的XX变量(写明A样本均值与样本误差)显著性高于常模总体均值)或对比变量(写明B样本均值与样本误差),t/F/Z/卡方值=XX,p值XX<0.05,效应量值=XXX。
决策:拒绝H0/不拒绝H0
结论:根据情况写明。比如改良新品种产品显著提高。”
05
—
假设检验的“陷阱”
1、小概率原理虽然是人们总结出来实用性很强的原理,但依然不能忽视小概率“灰犀牛”的存在,也是假设检验本身的缺陷所在。
2、样本、样本、样本,幸运者偏差,只要数据分析师愿意,TA可以给你一个你想要的结论,利用系统性偏差,违反了随机原则而导致的代表性误差,所以老板或业务不懂点统计学,真的会被忽悠咯~
3、显著水平的设置要根据实际情况。
4、为啥验证要分什么t\Z\F\卡方\非参数检验,就是告诉咱们不要觉得正态分布是神就可以随便套用,用对检验方法是为了降低误差。还记不记得你是怎么被平均的吗?







