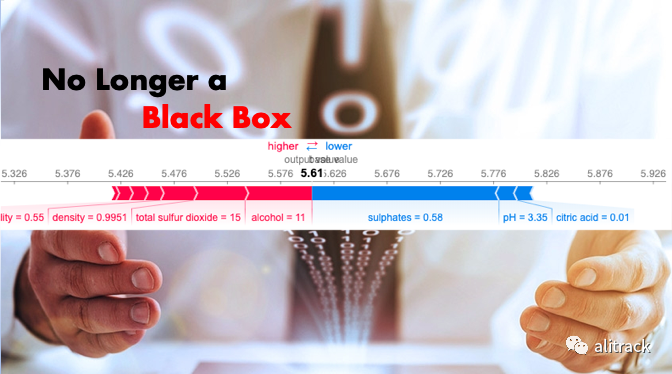
更好的可解释性才有更好的应用
你训练的模型容易理解吗?复杂的机器学习算法通常可以产生准确的预测,但其臭名昭著的“黑匣子”性质根本无助于应用。想一想:如果你让我吞下一个黑色药丸而不告诉我里面有什么,我当然不想吞下它。模型的可解释性就像药瓶上的标签。我们需要使我们的有效药丸透明化,以便于应用。
我们该怎么做?和 LIME,InterpretML,或 ELI5 一样,SHAP 值也是可解释人工智能或可信人工智能的重要工具,这是人工智能的新兴发展。在本文中,我将向您展示什么是 Shapley 值以及 SHAP(Shapley Additive exPlanations)值是如何从 Shapley 概念中产生的。我将向您展示 SHAP 值如何提高模型透明度。本文最后还附带了 Python 代码,以便您在应用程序中产生不错的效果,或者您可以在Github(https://github.com/dataman-git/codes_for_articles/blob/master/Explain your model with the SHAP values for article.ipynb)中下载 Notebook 。
什么是 Shapley 值?
让我用一个故事来解释 Shapley 值:假设 Ann、Bob 和 Cindy 一起将一根 38 英寸的“Error”木原木锤到地上。下班后,他们去当地的一家酒吧喝酒,我这个数学家也加入了他们。我问了一个很奇怪的问题:“每个人的贡献(英寸)是多少?”
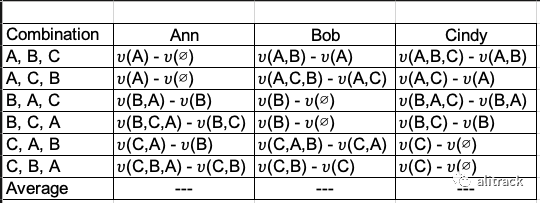
如何回答这个问题?我列出了所有排列并得出了表 A 中的数据。(有些人问我如何得出这个表。请参阅文章末尾的注释。)当顺序是 A、B、C 时,三者的边际贡献分别为 2、32、4 英寸。
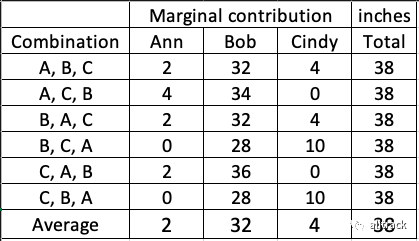
该表显示(A,B)或(B,A)的联盟为 34 英寸,因此 C 对该联盟的边际贡献为 4 英寸。我取了每个人所有排列的平均值来得到每个人的贡献:Ann 是 2 英寸,Bob 是 32 英寸,Cindy 是 4 英寸。**这就是计算 Shapley 值的方法:它是所有排列的边际贡献的平均值。**我将在本文末尾用正式的数学术语描述计算。但是现在,让我们看看它是如何应用于机器学习的。
我将木头日志称为错误日志有一个特殊的原因:它是机器学习上下文中的损失函数
。误差
是实际值与预测值之间的差异。锤子是攻击错误日志的预测器。我们如何衡量锤子(预测器)的贡献?Shapley 值!
从 Shapley 值到 SHAP(Shapley Additive exPlanations)
SHAP(Shapley Additive exPlanations)值得拥有自己的空间,而不是 Shapley 值的扩展。通过若干模型解释性的方法(1[1],2[2],3[3],4[4],5[5],6[6],7[7]),Lundberg and Lee (2016)[8]提出的 SHAP 值作为一个统一的方法来解释任何机器学习模型的输出。这里值得一提的三个好处。
第一,全局可解释性——集体 SHAP 值可以显示每个预测变量对目标变量的积极或消极贡献。这类似于变量重要性图,但它能够显示每个变量与目标的正负关系(请参阅下面的 SHAP 值图)。 第二,局部可解释性——每个观察都有自己的一组 SHAP 值(参见下面的单个 SHAP 值图)。这大大增加了它的透明度。我们可以解释为什么一个案例会收到它的预测以及预测变量的贡献。传统的变量重要性算法只显示整个群体的结果,而不是每个个体的结果。局部可解释性使我们能够查明和对比这些因素的影响。 第三,可以为任何基于树的模型计算 SHAP 值,而其他方法使用线性回归或逻辑回归模型作为替代模型。
模型可解释性并不意味着因果关系
重要的是要指出 SHAP 值不提供因果关系。在“识别因果关系”系列文章中,我展示了识别因果关系的计量经济学技术。这些文章涵盖以下技术:回归不连续性(参见“通过回归不连续性识别因果关系[9]”)、差异差异(DiD)(参见“通过差异差异识别因果关系[10]”)、固定效应模型(参见“通过固定[11]差异识别因果关系[12]”)效应模型[13]”),以及具有因子设计的随机对照试验(参见“变革管理实验设计[14]”)。
数据可视化和模型可解释性
数据可视化和模型可解释性是数据科学项目中不可或缺的两个方面。它们是双筒望远镜,可帮助您查看数据中的模式和模型中的故事。

如何在 Python 中使用 SHAP?
我将使用 Kaggle.com 中的红酒质量数据[15]进行分析。该数据集的目标值是从低到高(0-10)的质量等级。输入变量是每个葡萄酒样品的含量,包括固定酸度、挥发性酸度、柠檬酸、残糖、氯化物、游离二氧化硫、总二氧化硫、密度、pH、硫酸盐和酒精。有 1599 种葡萄酒样品。
在本文中,我构建了一个随机森林回归模型,并将在 SHAP 中使用 TreeExplainer。一些读者询问是否有一个适用于任何 ML 算法的 SHAP Explainer——无论是基于树的算法还是非基于树的算法。就在这里。它被称为*KernelExplainer。*你可以阅读我的第二篇文章“用 SHAP 值解释任何模型——使用 KernelExplainer[16] ”,其中我表明如果你的模型是基于树的机器学习模型,你应该使用TreeExplainer()
经过优化以快速渲染的树解释器结果。如果您的模型是深度学习模型,请使用深度学习解释器DeepExplainer()
。对于所有其他类型的算法(例如 KNN),请使用KernelExplainer()
。
想要深入了解机器学习算法的读者,可以查看我的帖子“我的关于随机森林、梯度提升、正则化和 H2O.ai 的讲义[17]”。对于深度学习,请查看“以回归友好的方式解释深度学习[18]”。对于 RNN/LSTM/GRU,请查看“股票价格预测的 RNN/LSTM/GRU 技术指南[19]”。
SHAP 值适用于连续或二进制目标变量的情况。二进制案例在[此处](https://github.com/dataman-git/codes_for_articles/blob/master/Explain your model with the SHAP values for article.ipynb "此处")的 Notebook 中实现。
import pandas as pd
import numpy as np
np.random.seed(0)
import matplotlib.pyplot as plt
df = pd.read_csv('/winequality-red.csv') # Load the data
from sklearn.model_selection import train_test_split
from sklearn import preprocessing
from sklearn.ensemble import RandomForestRegressor
# The target variable is 'quality'.
Y = df['quality']
X = df[['fixed acidity', 'volatile acidity', 'citric acid', 'residual sugar','chlorides', 'free sulfur dioxide', 'total sulfur dioxide', 'density','pH', 'sulphates', 'alcohol']]
# Split the data into train and test data:
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size = 0.2)
# Build the model with the random forest regression algorithm:
model = RandomForestRegressor(max_depth=6, random_state=0, n_estimators=10)
model.fit(X_train, Y_train)
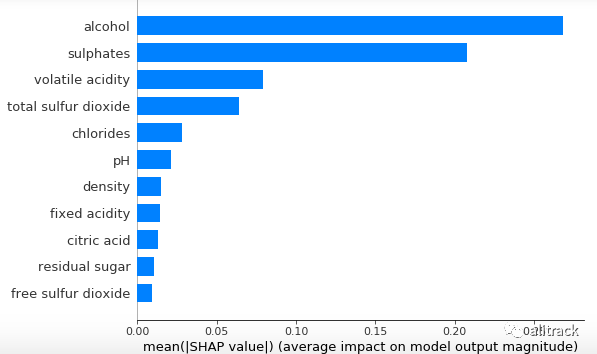
(A) 变量重要性图——全局可解释性
在shap.summary_plot
与功能plot_type=”bar”
让你产生变量重要性情节。变量重要性图按降序列出最重要的变量。顶部变量比底部变量对模型的贡献更大,因此具有较高的预测能力。
import shap
shap_values = shap.TreeExplainer(model).shap_values(X_train)
shap.summary_plot(shap_values, X_train, plot_type="bar")
读者可能想要输出任何汇总图。虽然 SHAP 没有内置函数,但您可以使用matplotlib
以下命令输出绘图:
import matplotlib.pyplot as plt
f = plt.figure()
shap.summary_plot(rf_shap_values, X_test)
f.savefig("/summary_plot1.png", bbox_inches='tight', dpi=600)
SHAP 值图可以进一步显示预测变量与目标变量的正负关系。该代码shap.summary_plot(shap_values, X_train)
生成以下图:
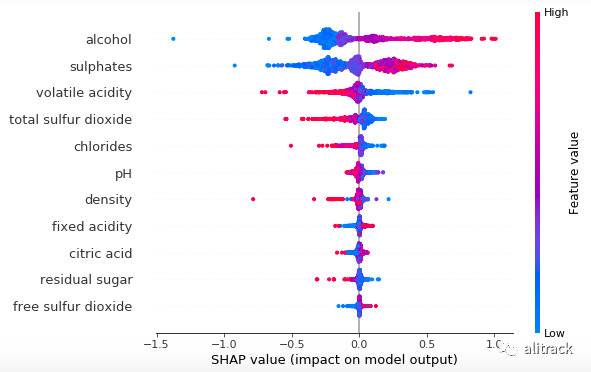
该图由训练数据中的所有点组成。它展示了以下信息:
*特征重要性:*变量按降序排列。 影响:水平位置显示该值的影响是否与更高或更低的预测相关联。 *原始值:*颜色显示该变量对于该观察值是高(红色)还是低(蓝色)。 相关:一个高的“酒精”含量水平具有较高的和积极的质量等级的影响。“高”来自红色,“正面”影响显示在 X 轴上。同样,我们会说“挥发性酸度”与目标变量负相关。
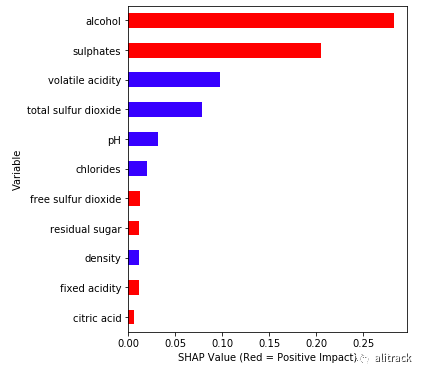
**简化图:**为了便于解释,我做了以下简化版本。它突出了颜色的相关性。红色表示特征与目标变量正相关。python 代码在文末提供给有兴趣的读者。
(B) SHAP 依赖图——全局可解释性
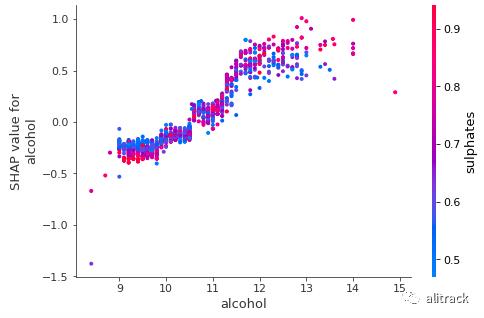
您可能会问如何显示部分依赖图。部分依赖图显示了一个或两个特征对机器学习模型的预测结果的边际效应 ( JH Friedman 2001[20] )。它告诉目标和特征之间的关系是线性的、单调的还是更复杂的。为了创建依赖图,您只需要一行代码:shap.dependence_plot(“alcohol”, shap_values, X_train)
. 该函数会自动包含另一个与您选择的变量交互最多的变量。下图显示“酒精”与目标变量之间存在近似线性的正趋势,“酒精”与“硫酸盐”频繁相互作用。
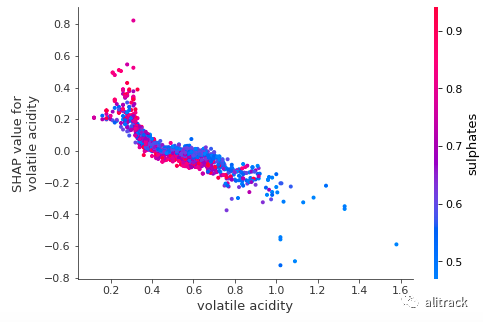
假设你想知道“挥发性酸度”和它相互作用最多的变量,你可以这样做shap.dependence_plot(“volatile acidity”, shap_values, X_train)
。下图显示“挥发性酸度”与目标变量之间存在近似线性但负相关的关系。这种负相关已经在变量重要性图图表 (K) 中得到了证明。
(C) 个体 SHAP 值图——局部可解释性
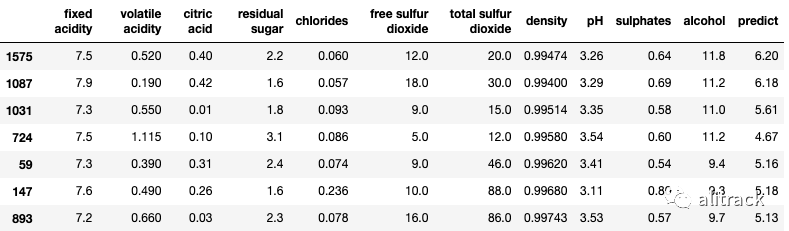
为了向您展示如何在个别情况下完成 SHAP 值,我将执行几个观察。我随机选择了一些观察结果,如下表 B 所示:
# Get the predictions and put them with the test data.
X_output = X_test.copy()
X_output.loc[:,'predict'] = np.round(model.predict(X_output),2)
# Randomly pick some observations
random_picks = np.arange(1,330,50) # Every 50 rows
S = X_output.iloc[random_picks]
S
如果您使用 Jupyter notebook,则需要使用 initjs() 对其进行初始化。为了节省空间,我编写了一个小函数shap_plot(j)
来执行表 B 中观测值的 SHAP 值。
# Initialize your Jupyter notebook with initjs(), otherwise you will get an error message.
shap.initjs()
# Write in a function
def shap_plot(j):
explainerModel = shap.TreeExplainer(model)
shap_values_Model = explainerModel.shap_values(S)
p = shap.force_plot(explainerModel.expected_value
, shap_values_Model[j], S.iloc[[j]])
return(p)
让我一步一步地引导你完成上面的代码。以上shap.force_plot()
取三个值:
基值( explainerModel.expected_value[0]
)SHAP 值( shap_values_Model[j][0]
)特征值矩阵 ( S.iloc[[j]]
)。
基值或期望值是模型输出在训练数据上的平均值X_train
。它是下图中使用的基值。
当我执行时,shap_plot(0)
我得到了表 B 第一行的结果:

让我详细描述一下这个优雅的情节:
输出值是该观察(在表 B 中的第一行的预测是 6.20)的预测。 该基值:在原论文[21]解释说,基准值 E(y_hat)是“如果我们不知道电流输出的任何功能,就用预测值。” 换句话说,它是平均预测,或 mean(yhat)。您可能想知道为什么是 5.62。这是因为 Y_test 的平均预测为 5.62。您可以通过 Y_test.mean()
产生 5.62 来测试它。红色/蓝色:将预测推高(向右)的特征以红色显示,将预测推低的特征以蓝色显示。 酒精:对质量评级有积极影响。该酒的酒精度为 11.8(如表 B 第一行所示),高于平均值 10.41。所以它把预测推到了右边。 pH:对质量等级有负面影响。低于平均 pH 值 (=3.26 < 3.30) 将预测推向右侧。 硫酸盐:与质量等级呈正相关。低于平均硫酸盐 (= 0.64 < 0.65) 将预测推向左侧。 您可能想知道我们如何知道预测变量的平均值。请记住,SHAP 模型是建立在训练数据集上的。变量的均值是: X_train.mean()
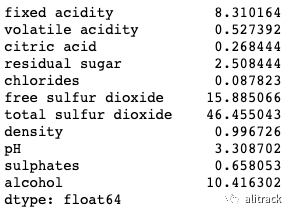
表 B 中第二次观察的结果是什么样的?让我们做shap_plot(1)
:

表 B 中的第三个观察结果如何?让我们做shap_plot(2)
:

只是在你感到无聊之前再做一次。表 B 中的第四个观察是这样的:shap_plot(3)

SHAP 值不能做什么
自从我发表了这篇文章、它的姊妹文章用 SHAP 值解释任何模型——使用 KernelExplainer[22] 以及最近的发展用更优雅的图表的 SHAP[23] ,读者与我分享了他们与客户会面时遇到的问题。问题不是关于 SHAP 值的计算,而是观众认为 SHAP 值可以做什么。一个主要评论是“您能否确定我们制定战略的驱动因素?”
上述评论是有道理的,表明数据科学家已经提供了有效的内容。然而,这个问题涉及相关性和因果关系。SHAP 值不识别因果关系,通过实验设计或类似方法可以更好地识别因果关系。有兴趣的读者,请阅读我的另外两篇文章变革管理的实验设计[24]或机器学习还是计量经济学?[25]
尾注:数学形式的 Shapley 值
二十多年前,当我还是一名研究生学习合作游戏和 Shapley 价值时,我不太确定是否有任何实际应用,但我被 Shapley 价值概念的优雅所吸引。二十年后,我看到 Shapley 价值概念成功地应用于机器学习。在上面的故事中,我用通俗的语言来描述它,这里我将用数学的形式来解释它。
Lloyd Shapley[26] 在 1953 年为合作博弈提出了这个解决方案概念。Shapley 想计算每个参与者在联盟博弈中的贡献。假设有N
个玩家并且S
是这 N 个玩家的子集。而v(s)
为S
玩家的贡献。当玩家 i
加入S
时,玩家i
的边际贡献为 v(S∪{i}) − v(S)。如果我们对可以形成联盟的可能不同排列的贡献取平均值,我们得到玩家i的正确贡献:
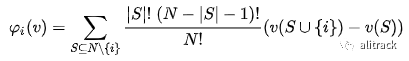
为了实现公平的贡献,Shapley 建立了以下四个公理:
公理 1:效率(Efficiency)。所有代理的 Shapley 值的总和等于总联盟的值。 公理 2:对称性(Symmetry)。所有玩家都有公平的机会加入游戏。这就是为什么上面的表 A 列出了所有玩家的排列。 公理 3:傀儡(Dummy)。如果玩家i对任何联盟 S 没有贡献,则玩家i的贡献为零,即*φᵢ(v)=0。*显然我们需要设置边界值。 公理 4:可加性。对于任何一对游戏v,w:φ(v+w)=φ(v)+φ(w),其中对所有S, (v+w)(S)=v(S)+w(S)。此属性使我们能够进行简单的算术求和。
我将 Shapley 值计算应用于表 (A) 以获得边际贡献:
在现实生活中,很难让三个锤子反复轮流记录表 A 的 Shapley 值。然而,在机器学习环境中这是很自然的。让我们用随机森林或梯度提升算法来说明这个概念。变量在模型树中按顺序或重复进入机器学习模型。在树生长的每一步中,算法都会平等地评估所有变量中的每一个,以选择贡献最大的变量。建造了数千棵树木。可以想象,变量的各种排列都是可用的。因此可以计算每个变量的边际贡献。
如何生成简化版?
对于对代码感兴趣的读者,我将其提供如下:
def ABS_SHAP(df_shap,df):
#import matplotlib as plt
# Make a copy of the input data
shap_v = pd.DataFrame(df_shap)
feature_list = df.columns
shap_v.columns = feature_list
df_v = df.copy().reset_index().drop('index',axis=1)
# Determine the correlation in order to plot with different colors
corr_list = list()
for i in feature_list:
b = np.corrcoef(shap_v[i],df_v[i])[1][0]
corr_list.append(b)
corr_df = pd.concat([pd.Series(feature_list),pd.Series(corr_list)],axis=1).fillna(0)
# Make a data frame. Column 1 is the feature, and Column 2 is the correlation coefficient
corr_df.columns = ['Variable','Corr']
corr_df['Sign'] = np.where(corr_df['Corr']>0,'red','blue')
# Plot it
shap_abs = np.abs(shap_v)
k=pd.DataFrame(shap_abs.mean()).reset_index()
k.columns = ['Variable','SHAP_abs']
k2 = k.merge(corr_df,left_on = 'Variable',right_on='Variable',how='inner')
k2 = k2.sort_values(by='SHAP_abs',ascending = True)
colorlist = k2['Sign']
ax = k2.plot.barh(x='Variable',y='SHAP_abs',color = colorlist, figsize=(5,6),legend=False)
ax.set_xlabel("SHAP Value (Red = Positive Impact)")
ABS_SHAP(shap_values,X_train)
代码产生这个图:

原文:Explain Your Model with the SHAP Values
链接:https://towardsdatascience.com/explain-your-model-with-the-shap-values-bc36aac4de3d
作者:Dr. Dataman
参考资料
1: https://www.kdd.org/kdd2016/papers/files/rfp0573-ribeiroA.pdf
[2]2: https://link.springer.com/article/10.1007/s10115-013-0679-x
[3]3: https://arxiv.org/pdf/1704.02685.pdf
[4]4: https://www.andrew.cmu.edu/user/danupam/datta-sen-zick-oakland16.pdf
[5]5: https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0130140
[6]6: https://onlinelibrary.wiley.com/doi/abs/10.1002/asmb.446
[7]7: https://blog.datadive.net/interpreting-random-forests/
[8]Lundberg and Lee (2016): https://papers.nips.cc/paper/7062-a-unified-approach-to-interpreting-model-predictions.pdf
[9]通过回归不连续性识别因果关系: https://medium.com/@Dataman.ai/identify-causality-by-regression-discontinuity-a4c8fb7507df
[10]通过差异差异识别因果关系: https://medium.com/@Dataman.ai/identify-causality-by-difference-in-differences-78ad8335fb7c
[11]通过固定: https://medium.com/@Dataman.ai/identify-causality-by-fixed-effects-model-585554bd9735
[12]差异识别因果关系: https://medium.com/@Dataman.ai/identify-causality-by-difference-in-differences-78ad8335fb7c
[13]效应模型: https://medium.com/@Dataman.ai/identify-causality-by-fixed-effects-model-585554bd9735
[14]变革管理实验设计: https://towardsdatascience.com/design-of-experiments-for-your-change-management-8f70880efcdd
[15]红酒质量数据: https://www.kaggle.com/uciml/red-wine-quality-cortez-et-al-2009
[16]用 SHAP 值解释任何模型——使用 KernelExplainer: https://towardsdatascience.com/explain-any-models-with-the-shap-values-use-the-kernelexplainer-79de9464897a
[17]我的关于随机森林、梯度提升、正则化和 H2O.ai 的讲义: https://medium.com/analytics-vidhya/a-lecture-note-on-random-forest-gradient-boosting-and-regularization-834fc9a7fa52
[18]以回归友好的方式解释深度学习: https://levelup.gitconnected.com/a-tutorial-to-build-from-regression-to-deep-learning-b7354240d2d5
[19]股票价格预测的 RNN/LSTM/GRU 技术指南: https://medium.com/swlh/a-technical-guide-on-rnn-lstm-gru-for-stock-price-prediction-bce2f7f30346
[20]JH Friedman 2001: https://statweb.stanford.edu/~jhf/ftp/trebst.pdf
[21]原论文: http://papers.nips.cc/paper/7062-a-unified-approach-to-interpreting-model-predictions.pdf
[22]用 SHAP 值解释任何模型——使用 KernelExplainer: https://towardsdatascience.com/explain-any-models-with-the-shap-values-use-the-kernelexplainer-79de9464897a
[23]用更优雅的图表的 SHAP: https://dataman-ai.medium.com/the-shap-with-more-elegant-charts-bc3e73fa1c0c?sk=7b4aee5d67f52db8ac824b07fd0b84a6
[24]变革管理的实验设计: https://towardsdatascience.com/design-of-experiments-for-your-change-management-8f70880efcdd
[25]机器学习还是计量经济学?: https://medium.com/analytics-vidhya/machine-learning-or-econometrics-5127c1c2dc53
[26]Lloyd Shapley: https://en.wikipedia.org/wiki/Lloyd_Shapley
欢迎关注公众号

有兴趣加群讨论数据挖掘和分析的朋友可以加我微信(witwall),暗号:入群

也欢迎投稿!






