昨天详细解释了SHAP，今天介绍下如果通过 Spark 来加快 SHAP Value 运算， 可以理解使用 PySpark Pandas UDF 加速机器学习任务续集，都属于通过 Spark 来加速机器学习范畴。更多参考文章：
Shapley 价值观是 Lloyd Shapley 于 1951 年提出的合作博弈理论的解决方案概念，他后来在 2012 年获得了诺贝尔经济学奖。决定经营企业的人）可以得到最佳分配，因为某些成员的贡献比其他成员多或少。总之，该理论指出，联盟中的每个参与者在该参与者可能参与的所有可能联盟下的平均边际贡献都是值得的。
随着对隐私和使用算法做出的决策的公平性的担忧增加，可解释性问题变得更加流行。经济学家无法想象的是，这个概念将彻底改变当今数据科学家解释机器学习模型的方式。机器学习算法是专用于预测任务的函数，它越精确，就越复杂，可解释性越低。将回归模型和决策树视为最简单的模型，将集成和深度神经网络视为最复杂的模型。
在 Shapley 值的上下文中，算法是联盟，模型的特征/变量是这个合作游戏的成员/参与者。与传统的特征重要性方法（如信息增益和基尼指数）相比，这些方法提供了关于特征相关性的洞察，沙普利值方法更进一步，增加了对特征相关性的洞察，每个特征如何影响单个数据点的预测和特征平均如何影响模型的结果。尽管如此，鉴于该概念涉及复杂的计算，对具有大量数据的数据集进行计算可能会变得乏味，有时根本不可行。
这篇博文的重点不是深入挖掘这些概念，而是展示如何扩展黑盒模型的可解释性，特别是使用 CatBoost、PySpark 和 Pandas UDF。最后，我们将回答以下问题：
是否可以缩放大型数据集中每个点的 Shapley 值，以便我们可以单独解释每个预测？ 如果我们使用 Spark 扩展/分发数据，计算时间是否会增加？ 从分布式数据和集中式数据获得的 Shapley 值之间有什么区别吗？
那么，让我们开始吧！
定义数据集
让我们从创建一个合成数据集开始。Scikit-learn 提供了一个非常好的 API，用于创建用于分类问题的数据集。这个 API 有很多选项（我们鼓励你检查这些选项），其中，我们选择了以下选项来生成一个包含一百万行、十个特征（其中七个是信息性的）和 2 类目标变量的数据集。
X, y = datasets.make_classification(n_samples=1000000, n_features=10, n_informative=7, n_classes=2, random_state=123)
该数据集将分为训练（80%）和测试（20%）。
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=123)
训练模型
现在，数据将用于创建训练 CatBoost 分类器模型所需的 Pool 对象。
train_c = Pool(data=X_train, label=y_train)test_c = Pool(data=X_test, label=y_test)
在这里，CatBoost 分类器使用超参数进行训练，以加快训练的执行速度。在本文中，我们不会关注这些参数的调整，也不会关注模型的性能。
model_c = CatBoostClassifier(iterations=1000, random_seed=123, boosting_type="Plain", bootstrap_type="Bernoulli", rsm=0.1, loss_function='Logloss', use_best_model=True, early_stopping_rounds=50)model_c.fit(train_c, eval_set=test_c, plot=True, verbose=False)
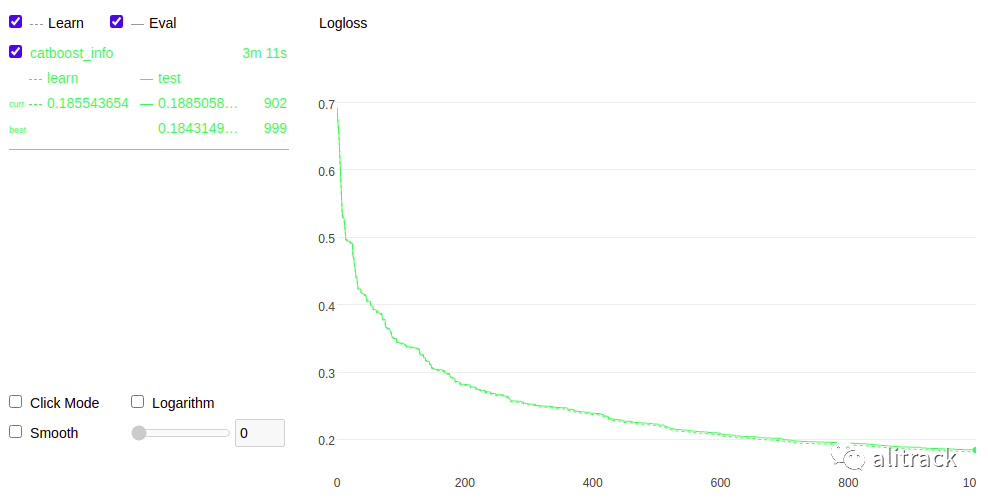
作为检查，让我们看看模型的最终精度。
accuracy = accuracy_score(model_c.predict(X_test), y_test)print(accuracy)0.934085
计算特征重要性
特征重要性是模型可解释性最常见和最简单的方法之一。为了在此处介绍的方法之间进行公平比较，用于计算的数据集将是完整的数据集。选择此选项是为了使计算时间更长，并且更少受到测量不准确的影响。
%%timeft_importance = model_c.get_feature_importance(Pool(X, y), prettified=True)CPU times: user 6.18 s, sys: 65.5 ms, total: 6.24 sWall time: 6.17 ssns.barplot(x=ft_importance['Feature Id'], y=ft_importance['Importances'])
功能重要性。
通过从 Catboost 模型中获取特征重要性的默认类型，可以观察到计算时间相对较短，正如预期的那样，由于方法的简单性。三个最重要的特征分别是 7、4 和 3。
计算 Shapley 值
最后我们来计算沙普利值。使用的 API 与 Feature Importance ( get_feature_importance ) 相同，只是添加了参数type=”ShapValues”。作为第一次观察，计算时间几乎是原来的两倍。鉴于计算的复杂性，这是意料之中的。
%%timeshap_values = model_c.get_feature_importance(Pool(X, y), type="ShapValues")CPU times: user 2min 33s, sys: 2.76 s, total: 2min 36sWall time: 14 s
变量shap_values是一个 numpy 矩阵，其中最后一列由表示预期值的相等元素组成。如果您需要有关这方面的更多信息，请在此处[1]查看此链接。换句话说，沙普利值将是这个 numpy 矩阵的所有元素，但最后一列。
expected_value = shap_values[0,-1]shap_values = shap_values[:,:-1]
shapley 值的汇总图如下图所示。可以看出特征重要性和 shapley 值之间存在相关性，但它们并不相同，这是已经预料到的，因为它们是不同的方法。例如，对模型输出有影响的三个主要特征分别是 shapley 值的 4、7 和 3，以及特征重要性的 7、4 和 3。
shap.summary_plot(shap_values, X)
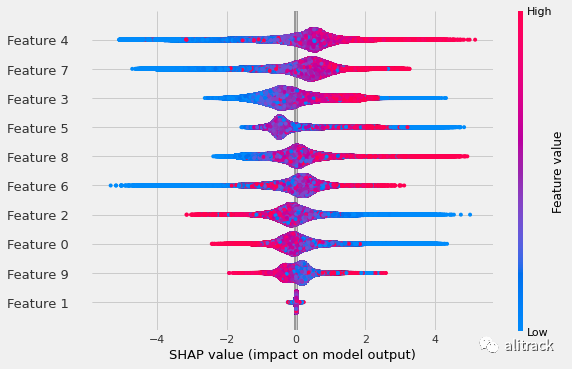使用常规计算类型（默认）的 Shapley 值。
shapley 值的另一个很酷的特性是特征贡献的总和等于值预测。让我们看看这个。这是我们数据集中第一个对象的特征贡献总和
sum(shap_values[0])2.366528338073737
这是我们数据集第一个对象的原始预测值
model_c.predict(X, prediction_type = 'RawFormulaVal')[0]2.366528338073735
正如我们所见，它们并不完全相等，但度量之间的差异几乎接近于零。
计算近似的 Shapley 值
计算shapley值时另一个有趣的方法是使用选项shap_calc_type = “Approximate”。这使得 shapley 值的计算速度更快，并且在特征和数据量非常大的情况下非常有用。本例中，由于数据量较小，计算时间略有差异。
%%timeshap_aprox = model_c.get_feature_importance(Pool(X, y), type="ShapValues", shap_calc_type="Approximate")CPU times: user 2min 36s, sys: 2.51 s, total: 2min 38sWall time: 13.7 sexpected_value_aprox = shap_aprox[0,-1]shap_aprox = shap_aprox[:,:-1]
下图显示了近似沙普利值的汇总图。由于计算速度更快，计算出的沙普利值会出现轻微失真。仔细查看此图会发现与之前未使用选项shap_calc_type = "Approximate"
的汇总图存在细微差异。例如，特征 0、2、6 和 8 不在同一位置。
shap.summary_plot(shap_aprox, X)
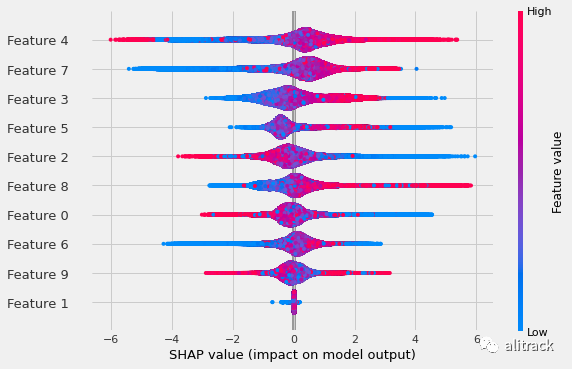Shapley 值使用计算类型近似。
Shapley 值的规模
那么让我们来看看魔法吧！第一步是使用 X 值创建 Spark 数据帧。
spark_df = spark.createDataFrame(pd.DataFrame(X))
下面的 Pandas UDF 是本文的主要技巧之一。API get_feature_importance
被嵌入
在函数shap_calc
中**，PySpark 函数withColumn()
将使用该函数在 Spark 数据帧中创建一个新列，其中包含以分布式方式计算的 shapley 值。
@pandas_udf(returnType=ArrayType(DoubleType()))def shap_calc(*cols): X = pd.concat(cols, axis=1).values shap = model_c.get_feature_importance( data=Pool(X), fstr_type="ShapValues" ) return pd.Series(shap.tolist())
如前所述，在此步骤中，将创建包含计算出的shapley值的列shap_array。
spark_df = spark_df.withColumn('shap_array', shap_calc(*model_c.feature_names_))
由于函数withColumn是惰性的，让我们执行一个简单的非惰性操作来了解在这种情况下计算 shapley 值所需的时间，并将其与之前的数字进行比较。正如预期的那样，执行计算所需的时间比之前执行的集中计算要短。此外，如果使用的工人数量更多，这种差异可能会更大。在此示例中，使用了八名工作人员。
%%timespark_df.cache().count()CPU times: user 7.64 ms, sys: 4.06 ms, total: 11.7 msWall time: 8.22 s1000000
同样，这里也可以使用选项shap_calc_type = "Approximate"
。将通过添加此参数创建另一个 Pandas UDF，并将其称为shap_calc_approx。
@pandas_udf(returnType=ArrayType(DoubleType()))def shap_calc_approx(*cols): X = pd.concat(cols, axis=1).values shap_v = model_c.get_feature_importance( data=Pool(X), fstr_type="ShapValues", shap_calc_type="Approximate", ) return pd.Series(shap_v.tolist())
在此步骤中，将在包含计算出的近似 shapley 值的 Spark 数据帧中创建另一列shap_array_approx。
spark_df = spark_df.withColumn('shap_array_approx', shap_calc_approx(*model_c.feature_names_))
让我们看看这个计算的时间。正如预期的那样，对于近似模式，这个时间甚至更短。
%%timespark_df.cache().count()CPU times: user 3.85 ms, sys: 5.06 ms, total: 8.91 ms
Wall time: 3.84 s
1000000
出于计算目的，本文的目的将在此结束。然而，这些计算出的沙普利值相对于之前显示的集中版本的表现仍然存在图形可视化。
为此，第一步是将计算出的沙普利值“分解”成列。下面的代码将创建一个包含 30 列的 Spark 数据框。前 10 个是 X 列。接下来的 10 列是从原始shap_array列“分解”出来的。最后 10 列是从原始shap_array_approx列“分解”出来的。
feat_size = X.shape[1]
feat_index = range(feat_size)
df_with_shap_values = spark_df.select(
*[sf.col(str(c)).alias(f'Feature {c}') for c in feat_index], # feature cols
*[sf.col('shap_array').getItem(c).alias(f"SHAP {c}") for c in feat_index], # SHAP for each feature col
*[sf.col('shap_array_approx').getItem(c).alias(f"SHAP APPROX {c}") for c in feat_index], # SHAP APPROX for each feature col
)
下一步是通过将所有这些值转换为 Numpy 然后获取相应的列来集中所有这些值。
np_values = df_with_shap_values.toPandas().to_numpy()
feat_values = np_values[:, :10]
shap_values = np_values[:, 10:20]
shap_values_approx = np_values[:, 20:]
最后，可以直观地观察到摘要图彼此不同，就像它们在集中版本中一样，但是与各自的集中版本相比，它们是相同的。
shap.summary_plot(shap_values, feat_values)
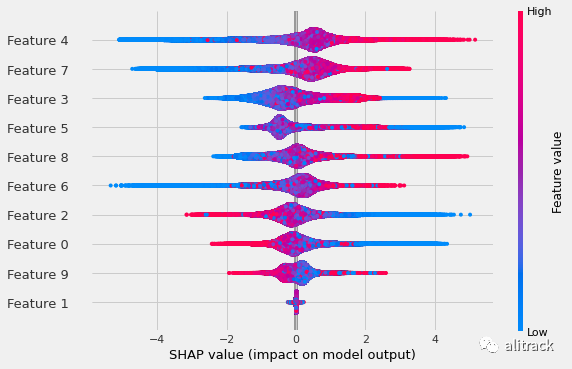使用常规计算类型分布的 Shapley 值（默认）。
shap.summary_plot(shap_values_approx, feat_values)
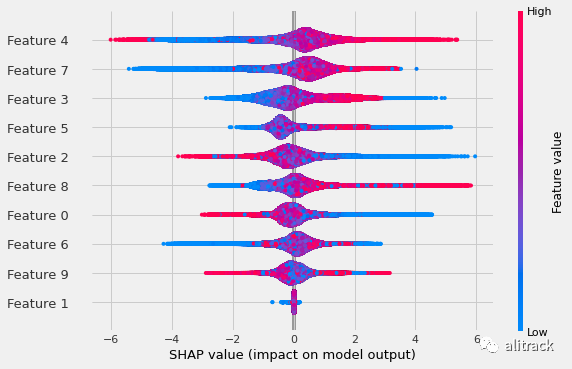使用计算类型近似分布的 Shapley 值。
结论
本文首先对特征重要性和沙普利值进行了简要比较。它们相似且相关但不相等。接下来，本文展示了 Shapley 值的四种计算方法：
1st - 使用计算默认集中（常规） 2nd - 使用计算近似集中 3rd - 使用计算默认分布（常规） 4th - 使用计算近似分布
可以看出，每次方法（从第一种到第四种）后，计算 Shapley 值的时间都会减少，其中第四种方法最快。另一方面，这种速度增益是有代价的：计算值的准确性略有下降。
最后，还可以观察到类似的计算方法（无论是集中式还是分布式）具有相同的计算值。这样，第一种和第三种方法产生相同的值，第二种和第四种方法也是如此。
原文：Shapley Values at Scale
链接：https://neowaylabs.github.io/data-science/shapley-values-at-scale/
作者：Igor Siqueira Cortez、Vitor Hugo Medeiros De Luca、Fernando Felix
参考资料
在此处: https://catboost.ai/docs/concepts/shap-values.html
