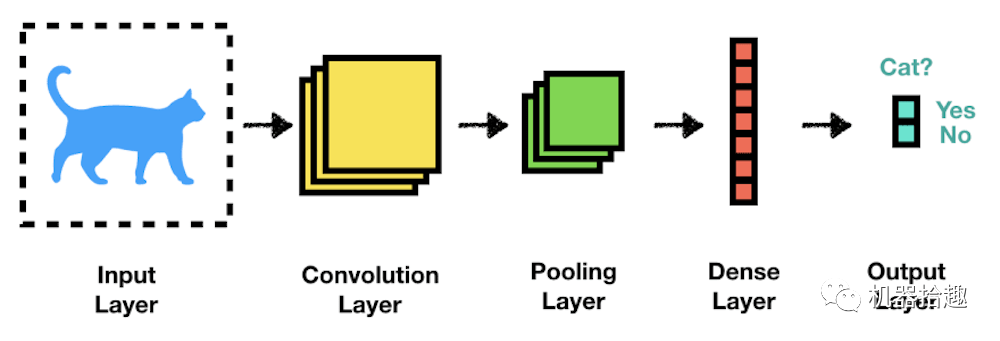
前言
深度学习在近两年大红大紫,主要功臣莫过于在计算机视觉computer vision领域的突破。而这里面,深度学习相对传统方式的最大优势,是通过神经网络结构实现特征的自动提取:直接把原始图像像素点输入,网络可以自动提取出有利于判断的特征。
实现这一切的关键,就是CNN(Convolutional Neural Networks)卷积神经网络。今天我们不展开来讲CNN,而是去理解CNN里面的一个重要性质 - 平移不变性。
认识大神
正文之前还是要先拜一拜CNN之父 - Yann LeCun,深度学习三巨头
之一、笑傲AI界的男人
、拥有中文译名最多的法国人
😄

CNN原理简介
卷积神经网络(Convolutional Neural Networks, CNN)是一类包含 卷积 计算且具有深度结构的 前馈神经网络 (Feedforward Neural Networks),是 深度学习 (deep learning)的代表算法之一 [1-2] 。卷积神经网络具有 表征学习 (representation learning)能力,能够按其阶层结构对输入信息进行平移不变分类(shift-invariant classification),因此也被称为”平移不变人工神经网络(Shift-Invariant Artificial Neural Networks, SIANN)“
卷积
首先我们来看什么是卷积
。我们将问题简化,假设原始图像像素矩阵如下:
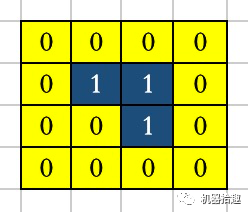
即高度为4,宽度为4,通道数是1。
假设filter是这样:
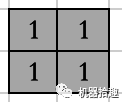
即shape=(2, 2, 1)
我们将filter放在原始图像的左上角
,做卷积操作(矩阵各个元素相乘,最后相加),结果为1x0+1x0+1x0+1x1=1
。
以此类推,如果我们将filter沿着原始图像从左到右,从上到下,依次扫描,每一次扫描都做一次卷积操作,则可以得到一个新的矩阵。
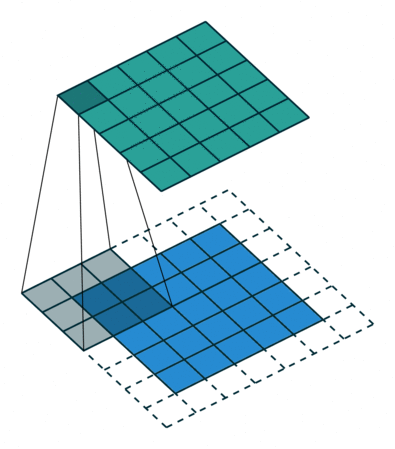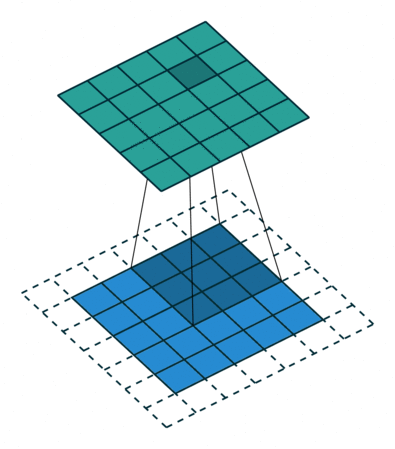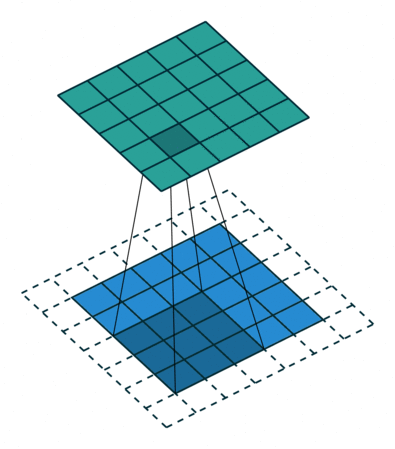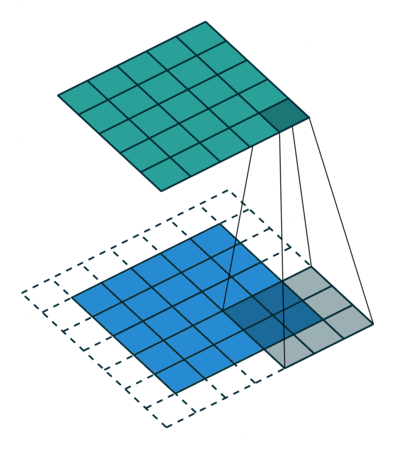
还是延续上面的例子,我们将扫描操作简化,no padding, no strides
,可以得到:
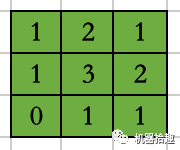
学过《信号与系统》的同学肯定能记得老师在课上经常讲的一句话:
时域卷积等于频域相乘
时域卷积等于频域相乘
时域卷积等于频域相乘
简单来说,CNN中的卷积操作,可以理解为多个不同类型的滤波器
的滑动窗口在图像全图滑动
,最后得到滤波后的结果。而这多个滤波器不是预先定义的,是网络通过不断的训练学习到的。
MaxPooling
CNN中还有一个非常重要的操作,叫MaxPooling,中文翻译为最大池化
,即取局部接受域中值最大的点。
这个操作很简单,还是继续上面的例子,我们把得到的结果做一次3x3的MaxPooling,即找出3x3格子里的最大值,即为3
。当然通常情况下也是需要做滑动操作的。
平移不变性
好了,了解了CNN的基本概念,我们可以来看平移不变性了。
首先解释下平移不变性 : 假设我们需要做图像识别,判断一张图片里面是猫还是狗:

那么不论这张图片里的猫或狗位于图像的哪个位置(上面还是下面,左边还是右边),我们训练好的神经网络都能够把它识别出来。而CNN恰好就具有这样的性质。
如何理解呢?
我们将上面的例子扩展一下,这里有三幅图片

这里的三角形分别位于中间,左边和上边。
我们还是以相同的2x2 filter做卷积

可以得到滤波后的结果
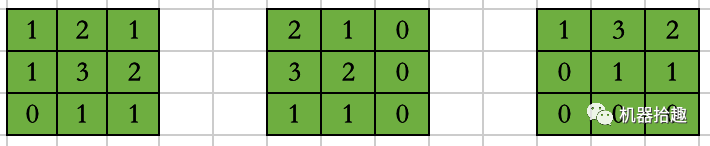
然后,再同时做3x3的MaxPooling,结果如何?

可以看到,不管三角形位于何处,最后都能得到相同的结果,而这个结果就是神经网络最后做图像识别的判断依据。
我们可以说,CNN的平移不变性,很大程度需要归功于MaxPooling,因为它是取的某个区域内的极大值。
展望
平移、旋转、scaling作为图像识别的三大经典问题,一直都是人们研究的热点。大神Yann LeCun陪伴Hinton三十年磨一剑,最终使用深度学习CNN很好的解决了这些问题,使得跌宕了几十年的深度神经网络重生,最终问鼎世界。
“深度神经网络既漂亮,又光亮透明”,LeCun说。
最后
欢迎订阅我的微信公众号“机器拾趣”,第一时间免费收到文章更新。

如果你喜欢我的文章,请点右下角“在看”,并且把它转发给你身边有需要的朋友。






