线段树：权值？合并？动态开点？没听说过

天空的代码世界 2021-09-20

808

线段树的三个高端算法，动态开点，储存权值，还可以合并。

零、背景

《leetcode 第 258 场算法比赛》的第四题是一道很有趣的题。

比赛的时候我使用贪心，把树转化为链，然后 DFS 通过了。

上上上篇文章《树上并查集》介绍了一个万能的树上并查集方法，甚至允许有重复权重值。

上上篇文章《RMQ LCA》介绍了一个 LCA 的方法，不过不支持重复权重值。

上篇文章《树递归编号》介绍了树递归编号的方法来解决问题，也不支持重复权重值。

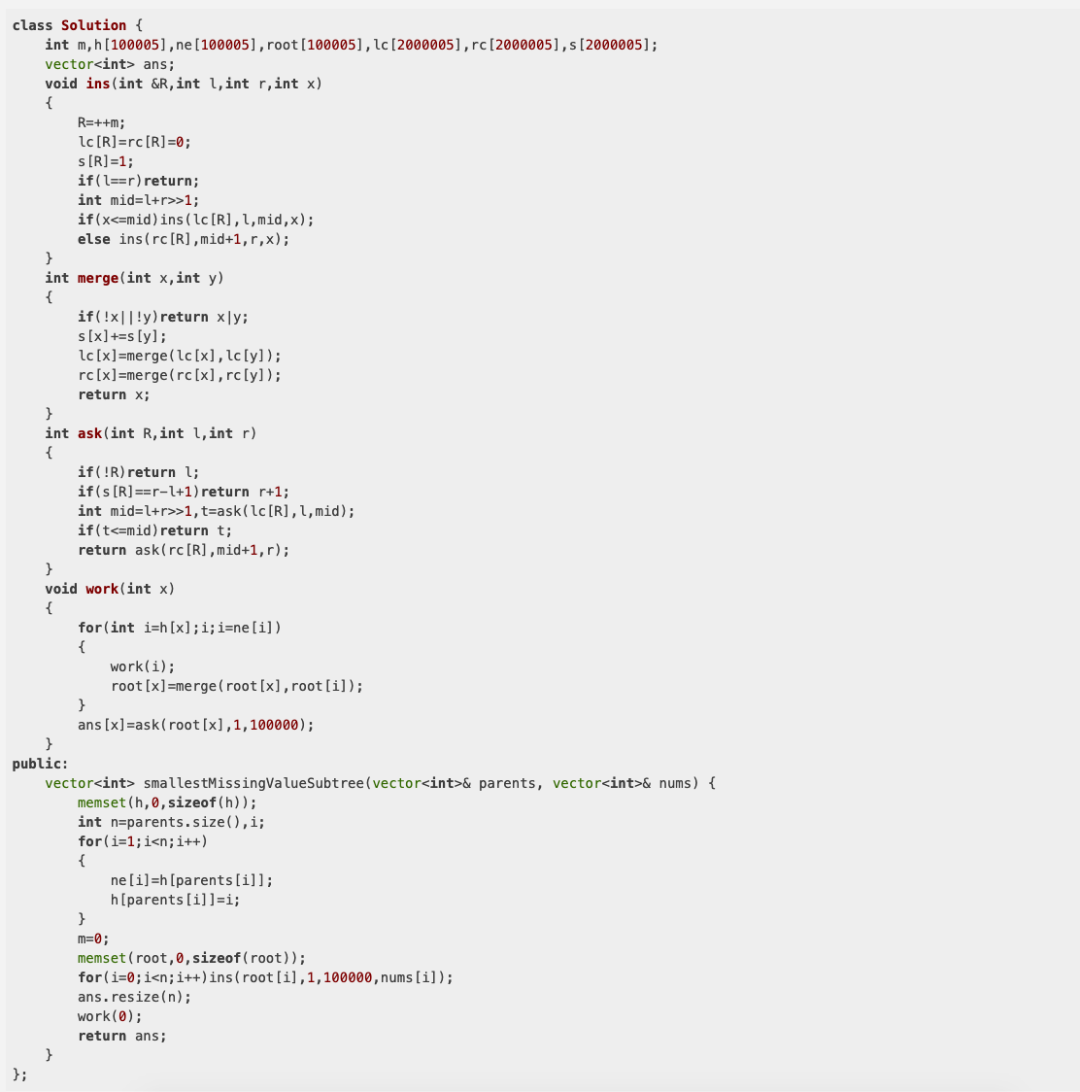
今天我再分享一个高端线段树的算法来解决这个问题。

一、题目

给一个有根树，每个节点有一个正整数值（互不相同）。

对于每个子树，问子树的节点值里面，最小的未出现的正整数是多少。

最小的未出现的正整数有个专业名称，叫做 mex（Minimum excludant）。

二、朋友圈

比赛后，有人给我发了一个题解。

我一看，完全看不懂。

于是发了一个朋友圈，问是啥算法。

朋友圈的大佬有人说是线段树合并，有人说是权值线段树。

我一脸懵逼，这是什么呢？怎么没听说过呢？

三、权值线段树

普通的线段树是给一个坐标位置，可以设置值。

然后可以查询区间最值或者区间和等问题。

权值线段树只关心下标这一个数据，用于统计不同下标出现的次数。

储存了这个数据后，就可以查询第 K 小/大值问题了。

当然，同样可以查询最小的未出现的正整数。

逻辑也很容易理解。

左子树区间大小与出现的数字个数相同，那显然答案在右区间（左区间是满的），否则肯定在左区间。

int Query(int x, int l, int r){
    if(x == 0) return l;
    if(V[x] == r - l + 1) return r + 1; 


    int mid = (l + r) >> 1;
    int leftAns = Query(L[x], l, mid);
    if(leftAns <= mid) return leftAns;


    return Query(R[x], mid + 1, r);
}
复制

四、线段树合并

一个线段树是一个不可拆分的完整的树。

前面插入的点将会影响后面区间的查询。

而面对子树问题时，左子树与右子树往往是没关系的。

这时候就需要对左子树与右子树分别建一个线段树，等分别求出各自的答案后，再合并出当前子树的线段树。

下面的代码是合并的权值线段树，将 y 为根的线段树合并到 x 为根的线段树。

int Merge(int x, int y) {
    if(x == 0 || y == 0) return x == 0 ? y : x;
    V[x] += V[y];
    L[x] = Merge(L[x], L[y]);
    R[x] = Merge(R[x], R[y]);
    return x;
}
复制

五、动态开点线段树

前面提到需要给每个子树创建一个线段树。

如果每个线段树初始化的时间复杂度是 O(N)
, 那建 n 个线段树的复杂度就是 O(N^2)
的时间了。

所以这里使用普通的线段树是不可行的。

然后就有人提出，既然树可以使用一个一维数组代替二维数组，那自然线段树也可以做到。

具体来说就是，线段树的某个节点存在值时，再开辟节点的内存空间。

这样对于稀疏矩阵，只需要很小的空间就可以表示一个线段树。

有时对于那种区间很大的线段树，离散化也解决不了，就可以采用动态开点的方式来储存线段树。

当然，这里我们使用动态开点方式储存的权值线段树。

非权值线段树应该一样可以表达的。

int L[M], R[M], V[M]; 


int index;
void Insert(int& x, int l, int r, int v) {
    x = ++index;
    L[x] = R[x] = 0;
    V[x] = 1;
    if(l == r) return ;
    int mid = (l + r) >> 1;
    if(v <= mid) {
        Insert(L[x], l, mid, v);
    } else {
        Insert(R[x], mid + 1, r, v);
    }
}
复制

六、查询 MEX

上面介绍了权值线段树、线段树的合并、动态开点线段树。

综合利用这三个数据结构或算法，我们就可以解决线段树查询子树 MEX 的问题了。

一开始，先给所有节点建立一个动态开点的权值线段树。

index = 0;
root.resize(n, 0);
for(int i = 0; i < n; i++) {
    Insert(root[i], 1, N, nums[i]);
}
复制

由于每个权值线段树高度是log(n)
，所以内存空间需要申请n log(n)
大小。

const int N = 100000;
const int M = 20 * N;
复制

之后，就可以递归的查询子树字段树，并合并子树线段树，从而递归的求出答案。

void Solver(int x) {
    for(auto v: g[x]) {
        Solver(v);
        root[x] = Merge(root[x], root[v]);
    }
    ans[x] = Query(root[x], 1, N);
}
复制