因为page 651 6.4.1 Generic Cache Memory Organization章节比较难以理解,我理解了很久才搞清楚,所以这篇笔记是对该章节的解释,本笔记并非按照文字顺序一对一翻译,而且根据我自己的理解思路所作。

如上图,假设一个计算机系统有一个存储,存储的地址有m个地址位,注意m是位(bit)的个数,这里“位”的用途是表示地址,因为计算机是二进制系统,所以总共可以表示2^m个地址。
现在,我们的问题是如何用一个缓存(cache)来存储这2^m个地址所对应的内容?解决这个问题之前,先要知道几个约束条件:
因为缓存比存储昂贵,处于性价比考虑,缓存的空间比存储的空间要少,不能将2^m个地址所对应的内容都缓存起来,所以缓存的内容是存储的内容的子集。
查询缓存必须有效率,不能每次都遍历缓存,所以要在缓存组织方式上动些头脑。
想象IP地址是怎么组织的——网络位+主机位,其实对于二进制数字的快速查询,思路都是一样的。
于是为了解决上面的问题,我们将m个地址位分为了3组(field),分别表示不同的含义,如下图(至于分别代表什么含义,下文再阐述)所要理解的是,t,s,b与m的含义一样,都是表示位数的个数,所以m = t + s + b。
t个地址位,可用T来表示,T = 2^t ,也就是说t个地址位可以表示 2^t个T的值,下同;
s个地址位,S = 2^s;
b个地址位,B = 2^b;

有了这个基础,我们就可以设计一个三维座标系统的组织方式,用于标识存储中每个数据块(block)的标识,其表示方式如下:
用s来表示某一个集合S的标识,对于每一个确定的集合S其标识是s个地址位的值,所以s个地址位总共可以表示 2^s个集合S
每个集合S有T行,用t来表示某一行T的标识,对于每一个确定的行T其标识是t个地址位的值,所以t个地址位总共可以表示 2^t行
每一行有B个block,用b来表示某个block B 的标识,对于每一个确定的Block其标识是b个地址位的值,所以b个地址位总共可以表示 2^b个block
总图如下:
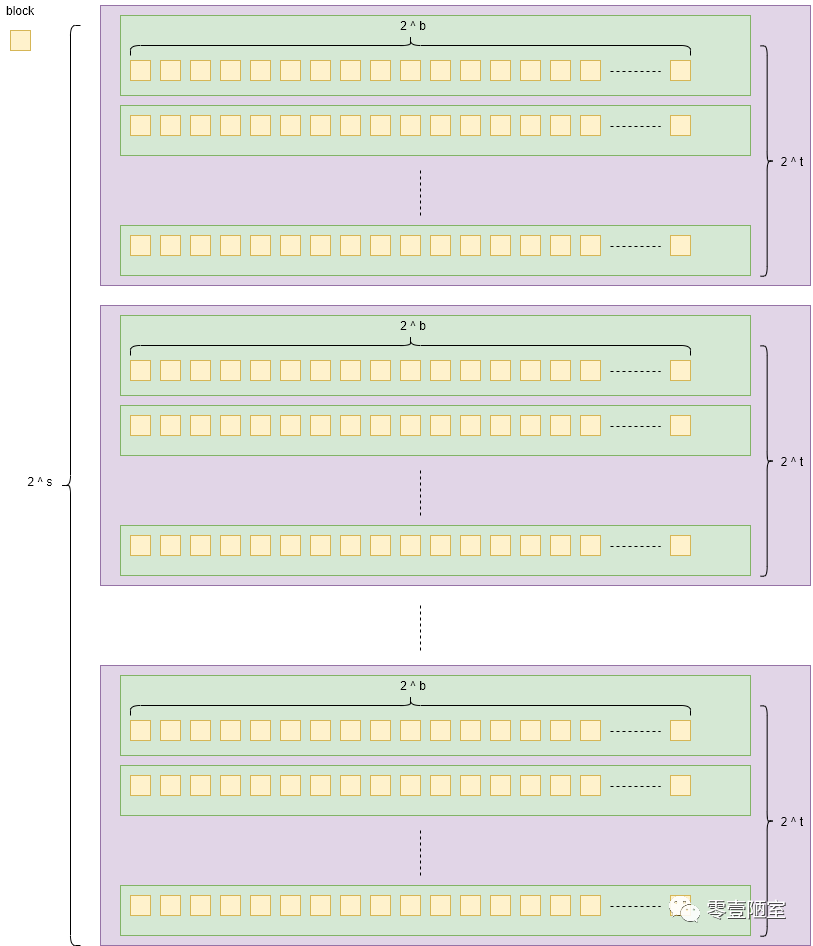
上图中Blocks的总数是 S * T * B,也就是说,按照上面的对地址位的划分方式,一个2^m个地址的计算机系统总共可以映射出S * T * B个Blocks。
这里假设C = S * T * B ,C就是这个2^m个地址的计算机系统的存储容量,如果一个block的大小是一个字节(byte),则这个计算机系统可以存储C字节的信息。
为了让这个存储组织结构能够适应缓存存储的需求,我们还需要作一些改造,一是新增valid位,用来包含一些特定意义的信息(meaningful inforamation),另外还要增加Tag位,用来记录T的值(kursk批注:T不是书中行号,下篇笔记再解释),所以上图的存储组织结构调整后就变成这样:
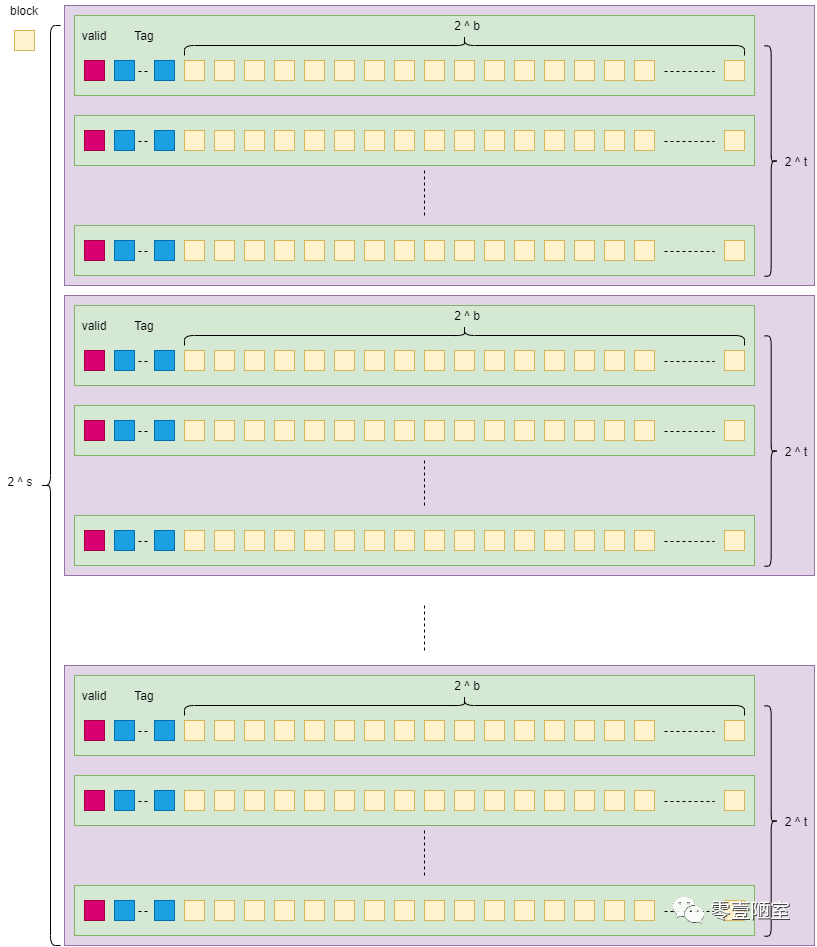
以上的笔记内容是我对原书该章节解读和理解,笔记的思路与书是一致的,但是模型细节不相同。
书中的缓存组织结构模型的一些细节解释得并不清楚,我在阅读很久并结合习题后才弄清楚很多细节问题,下面笔记的部分严格按照书中的缓存模型,回答让我思考很久的两个问题:
1、书中的“tag bits”是不是行号?
答:tag bits不是行号!tag bits与书中的行号E是两个不同的值。
在书中page 664 习题6.12中的例子很清楚,line 0和line 1都有多个tag,所以 tag 并不是行号。
2、page651 书中写到Each line consists of a data block of B = 2 ^ b bytes ,既然 B指定的是每行中Block的大小,那么page 652中 b block offset bits 又是怎么回事?这里的b到底控制的是Block的大小,还是偏移量offset
答:其实可以这样认为,每行(line)只有一个block(a data block),而这个block的大小是由b决定的,注意b是“位的个数”,所以每位的值就组成了偏移量,看看下面这个例子
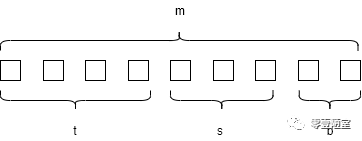
t是tag位,t=4;
s是set位,s=3
b是偏移位,b=2
因为b=2,所以B = 2 ^ 2 = 4,所以每行的block大小为 4 bytpes。另外,b 位所组成的值也是偏移量,如下图:
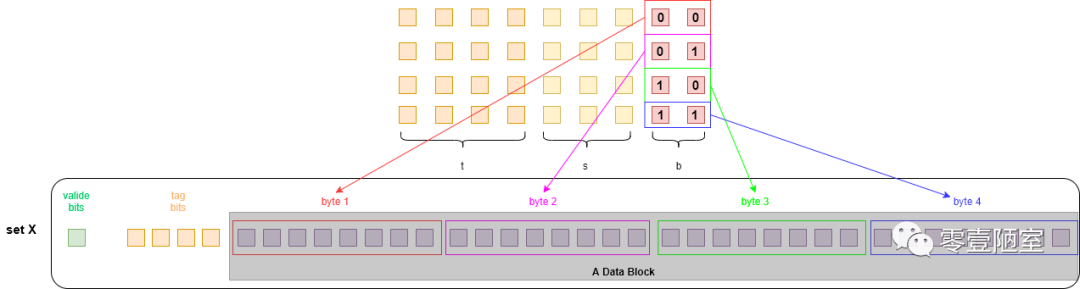
个人理解,6.4节重点介绍缓存组织结构的设计思路,这一思路的关键在于地址的划分与缓存组织结构的对应关系,书中有些细节不要太过推敲,例如page 656中为什么画两个block,block[0]和block[1]?我一度根据这个表以为有多个block,后来仔细想想,恐怕这种理解不对。
最后对本节内容进行小结,下文中的“缓存”指上一级的存储元件,“存储”指下一级的存储元件。
因为缓存的空间小于存储的空间,所以缓存组织结构设计的根本目标,是如何合理地将存储中的部分内容放置在缓存中,因为是“部分”,所以就要对存储的内容进行分组,让“同一组”的内容去竞争缓存中的空间,“合理”就体现在竞争机制上,竞争过程中IO越少越“合理”。
在缓存组织结构和竞争机制的设计中,有这样几项关键或有趣的设计:
存储中每个地址的都是唯一的,地址用于标识存储中的block,所以通过将地址中的位按 set bits和 tag bits分组(field),从而达到标识缓存中的内容的效果;
地址位中的set bits和tag bits是用来匹配缓存中的内容的唯一条件,书中多次出现这段表述,例如page 655 the concatenation of the tag and index bits uniquely identifies each block in memory.
匹配成功后,对应整行都会替换(竞争机制),page 655 the current line is replaced by the newly fetched line,但是也因为整行替换,所以才会出现 thrashing这种问题(kursk注:所以我觉得set bits和 tag bits的选择很重要,因为它们是分组的参数)
缓存组织结构模型(S, E, B, m),S、B、m来自于地址位,但是E却不是。






