二叉树的遍历有三种方法:递归、栈、Morris。Morris的优点在于它只需要O(1)的空间。是时候静下心,找个地方坐下来,认真学习一波了。
原理分析
二叉树的中序遍历遵循:左子树->根节点->右子树的顺序。
递归和栈的方法,只所以需要O(N)的空间,是因为需要维护访问的顺序,尤其是访问完左子树之后回到根节点这个顺序。
morris用了另一个方法来维护这个顺序,就是直接在左子树和根节点之间创建一个链接。这样,访问完左子树之后,就可以直接访问根。
下面,我们先把算法的流程过一遍,可能比较抽象,别担心,我们紧接着就用一个例子来说明该流程:
设置curr指针,表示当前节点,并初始化为root
如果curr不是None,检查curr是不是有左子节点
如果curr没有左子节点,打印curr节点,并把curr更新为curr的右子节点
如果curr有左子节点,将以左子节点为根节点的子树最右边的节点的右子节点设置为curr
将curr更新为curr的左子节点
例子分析
看完上面的流程,是不是有点晕,不怕,现在就看例子。
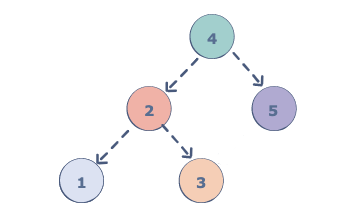
假如我们想要用Morris算法中序遍历上面的二叉树。我们先把curr初始化为根节点4。4因为有左子节点,所以要把以1-2-3这颗左子树最右边的的节点的右子节点设置为curr,即根节点4。并将curr更新为左子节点2。如下图所示:
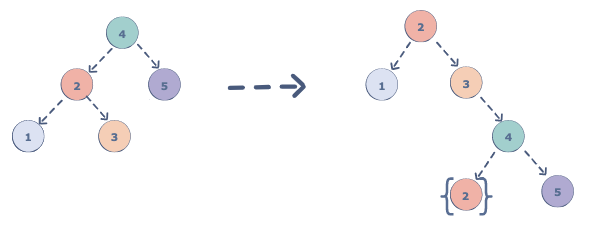
上图中{2}代表左子节点2和它所有的子节点。
现在的结构,访问完3节点后,能够继续访问节点4,正好是左->根->右顺序中的左->根。
然后继续,节点2有左子节点1,把它看成一颗单节点的二叉树,它本身就是这颗单节点的二叉树的最右边的节点,所以直接把它的右子节点设置成当前节点2。并将curr设置为1节点如下图所示:
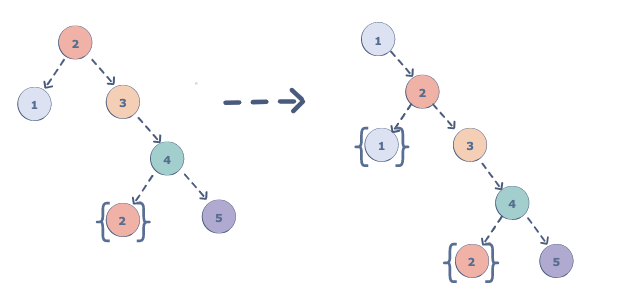
此时,我们需要打印节点1,因为它没有左子节点了。然后curr更新到1节点的右子节点2。
关键的地方来了。此时的节点2仍然有左子节点,但是我们知道2节点的左子树已经访问过了。不需要再次访问。那如何判断呢?
我们可以根据左子树最右边的节点的右子节点是不是当前节点来判断。
如果是,那就说明左子树已经访问过了。并且此时,我们可以顺手把之前手动添加的链接去掉。
既然2节点的左子树已经访问过,那么就打印2节点,并把curr更新为2节点的右子节点3。
节点3没有左子节点,所以直接打印3节点,并把curr设置为它的右子节点4。
此时,根据前面的规则,我们可以判断出来,4节点的左子树也已经访问过了。所以我们打印节点4,并将curr更新为4的右子节点5。
节点5没有左右子节点,所以简单打印5节点,完成中序遍历。
如果你看完上面的讲解还是有点晕,我建议你按照下面的代码实现,一步一步执行一下,在你的大脑中执行一下这个算法,验证算法的正确性。
另外,还是觉得不踏实,我建议你放弃问为什么这种算法就可以,你可以这样想,算法本身就是人为设计出来的,通过执行,发现它恰恰实现了中序遍历,也就是这是实验科学,不是理论科学。放过自己把。
代码实现
class Node:
def __init__(self, data):
self.data = data
self.left_node = None
self.right_node = None
def Morris(root):
curr = root
while(curr is not None):
if curr.left_node is None:
print curr.data,
curr = curr.right_node
else:
prev = curr.left_node
while(prev.right_node is not None and prev.right_node != curr):
prev = prev.right_node
if(prev.right_node is None):
prev.right_node = curr
curr = curr.left_node
else:
prev.right_node = None
print curr.data,
curr = curr.right_node
root = Node(4)
root.left_node = Node(2)
root.right_node = Node(5)
root.left_node.left_node = Node(1)
root.left_node.right_node = Node(3)
Morris(root)复制
Reference:
https://www.educative.io/edpresso/what-is-morris-traversal
往期精彩回顾







