滑动窗口算法最简单的教程（2）

在滑动窗口算法最简单的教程（1）中，我们已经知道了，滑动窗口要解决的问题就是重复计算。这一点是滑动窗口问题的核心思想。今天要讲的这道题，比之前的问题要复杂一丢丢，但是基本思想那是一样一样的。

1 先看问题

给定一个都是正数的数组和一个正数，找到长度最短的连续元素组成的子数组，使它的和大于或者等于。如果这样的子数组不存在，返回0。

为了便于理解，我们给出几个具体的例子。

例子1：

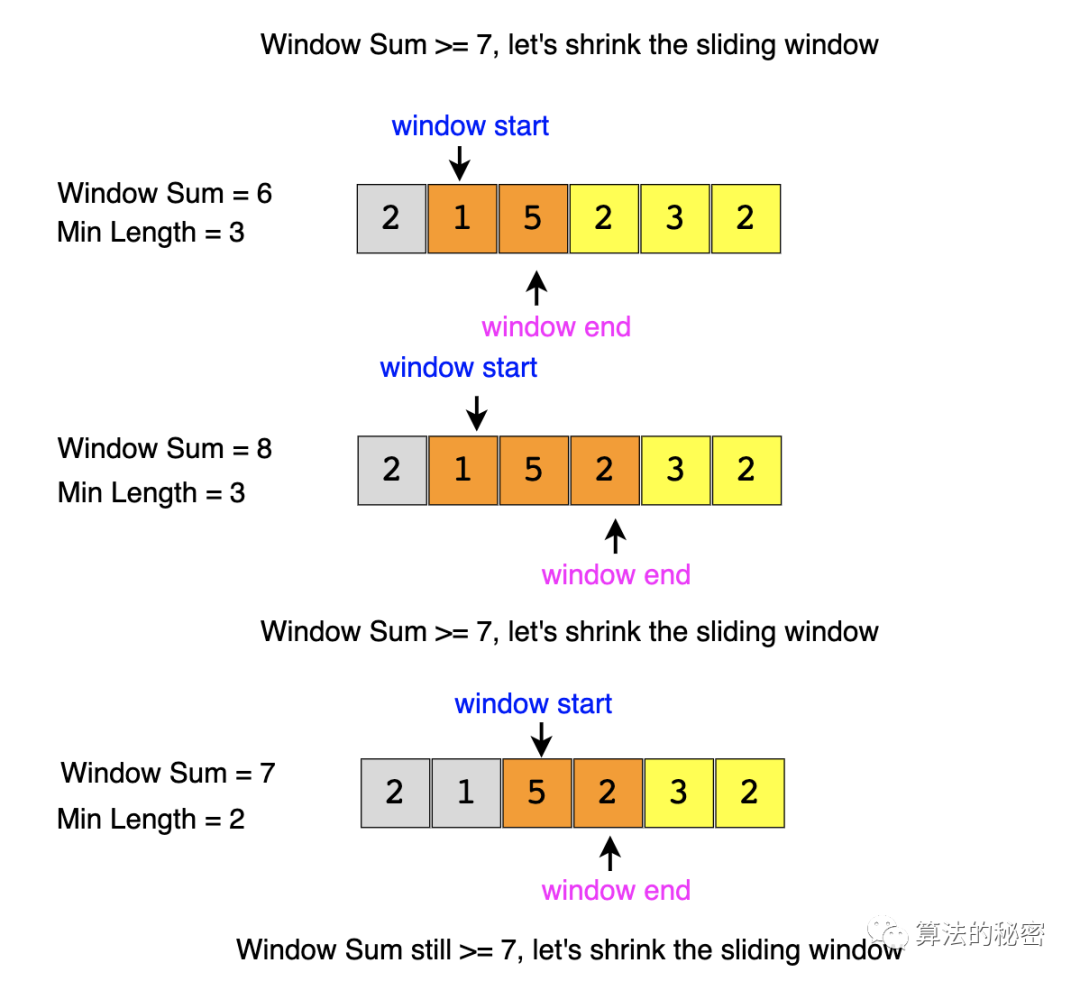
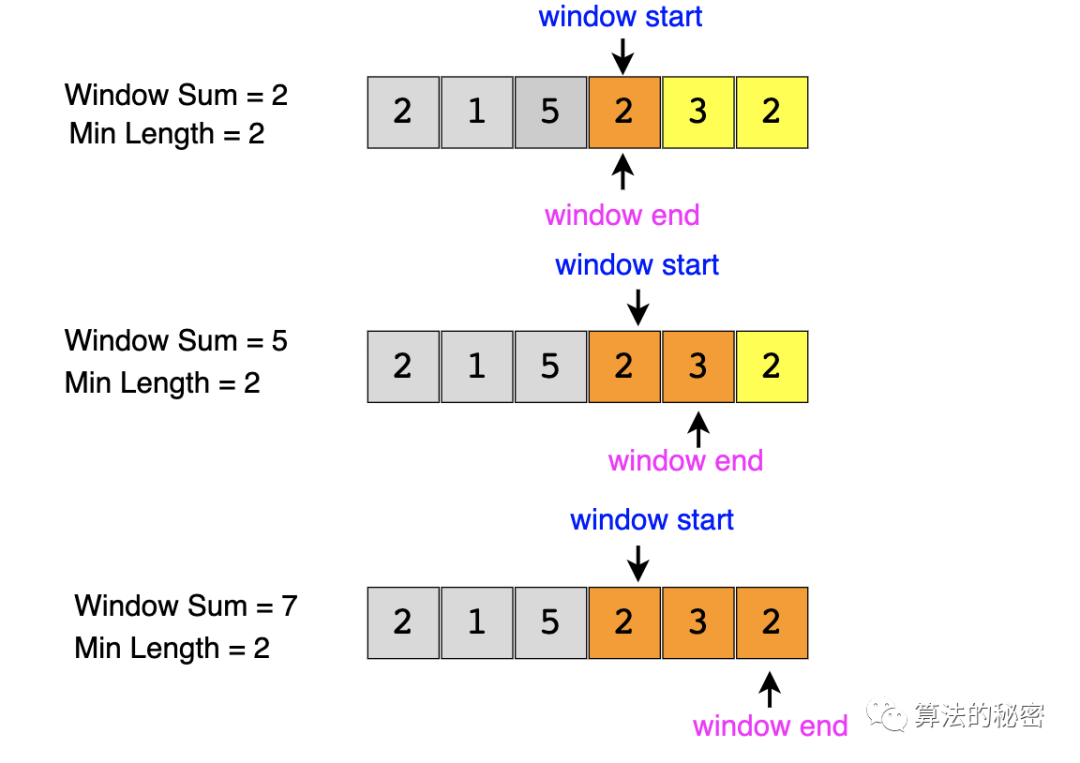
输入: [2, 1, 5, 2, 3, 2], S=7 输出: 2 解释: 和大于等于7的最小子数组是 [5, 2]

例子2：输入: [2, 1, 5, 2, 8], S=7 输出: 1 解释: 和大于等于7的最小子数组是 [8]

例子3：输入: [3, 4, 1, 1, 6], S=8 输出: 3 解释: 和大于等于8的最小子数组是 [3, 4, 1] 或者 [1, 1, 6]

2 思路分析

这个问题和滑动窗口算法最简单的教程（1）中的问题，有一点明显不同，就是滑动窗口的大小并不是固定的。窗口每滑动一步，窗口的起始点都要尽可能的收缩，因为我们要找的是最小的窗口。所以，我们的解决方案如下：

• 1、从数组起始处开始连续累加元素，直到元素的和大于或等于
• 2、这时得到的连续子数组就组成我们的当前滑动窗口。我们要做的就是找到最小的窗口，使得窗口内元素的和大于或等于。我们将当前滑动窗口的长度作为迄今为止最小的窗口长度（因为只有这一个窗口）。
• 3、然后，我们在窗口右端再加进来一个元素，相当于窗口右端前进了一步。
• 4、右端每前进一步，我们都尝试收缩窗口的左端，我们将一直收缩，直到窗口内元素的和再次小于。这么做的目的，正是为了找到最小的窗口。此时的收缩，可以理解成是在所有以当前窗口右端点为右端点的连续子数组中，查找符合条件的最小窗口。只不过这里，我们不用再从数组开头查找，而是直接从当前窗口左端点处开始查找。如果仔细体会，会发现，此时的滑动窗口算法，我们不仅复用了窗口内元素的求和，同时，也复用了窗口的左端点来避免从头开始的计算。左端的收缩也许要进行许多步，在每一步中，我们都需要做两件事儿：（1）检查一下当前窗口的长度是不是目前为止最小的，如果是，就记下来（2）将当前窗口左端的第一个元素从窗口中移除

以例子1为例，我们的算法可以示意如下：

3 代码实现

import math

def smallest_subarray_with_given_sum(s, arr):
  window_sum = 0
  min_length = math.inf
  window_start = 0

  for window_end in range(0, len(arr)):
    window_sum += arr[window_end]  # 累加下一个元素
    # 尽可能缩小窗口，直到窗口内元素的和小于S
    while window_sum >= s:
      min_length = min(min_length, window_end - window_start + 1)
      window_sum -= arr[window_start]
      window_start += 1
  if min_length == math.inf:
    return 0
  return min_length