有非常多的同学,包括小孩子都曾经或者正在觉得用代码实现某个算法就像是在做脑经急转弯——看过答案之后你会觉得非常简单,但自己就是写不出来>_<
问题到底是出在哪里了呢?本篇文章从一个非常简单,但却蕴含着十分重要的算法思想的归并排序
入手,以一个完全小白的视角来考虑一下我们实现这个算法的时候到底会遇到哪些坑,以及如何解决它们。
什么是归并排序?
为防止一部分小伙伴可能并不知道归并排序
是个啥,我们先来介绍一下。
归并排序
是一个非常经典的排序算法,这个算法特简单,一句话就可以描述完:将一个待排序数组分成两个子数组,先分别对两个子数组进行排序,然后再将两个排好序的子数组合并成一个大的排序数组。
简单的描述里隐藏着3个细节:
•细节1:问题的分解(Divide):如何将一个待排序数组拆分成两个子数组?
•细节2:子问题的解决(Conquer):如何对两个子数组进行排序?
•细节3:子问题的合并(Combine):如何将两个有序的子数组合并为一个大的有序数组?
下边分析一下上述3个细节
。
细节1
将一个数组拆分成两个子数组非常简单,只需要算出中间元素的下标,那我们可以规定:
•从数组开头的元素到中间元素属于一个子数组
•从中间元素的后一个元素开始,到数组最后一个元素属于另一个子数组
中间元素的下标 = (起始元素的下标 + 末尾元素的下标) 2
小贴士:这里请大家思考一下我们为什么不用数组中包含元素数量除以2的方式来计算中间元素的下标,如果以这种方式计算中间元素的下标的话会发生什么事情(友情提示:可以按照数组中包含元素数量是单数还是双数来分开讨论)。
细节2
细节2
其实很好解决,在对某个子数组进行排序时,可以将这个子数组继续分成两个子子数组,先对这两个子子数组进行排序,然后再将这两个排好序的子子数组进行排序,就完成了对子数组的排序。
子子数组怎么排?继续拆成两个更小的数组排呗。这里成功的进入了套娃模式,直到某个子子子...子数组里只包括1个元素就不用再拆了。
也就是说我们可以将子问题
继续拆分成多个子子问题
,然后进入套娃模式,直到某个子问题足够简单为止(本例中就是直到子数组中仅包含1个元素为止)。
当然,上边的描述不是很直观,我们具体举个例子看一下。
我们有一个无序数组[2, 7, 1, 4, 6, 5, 0, 4]:

这个数组包含8个元素,我们把它分成两个组:1组
和2组
,每个组都包含4个元素:
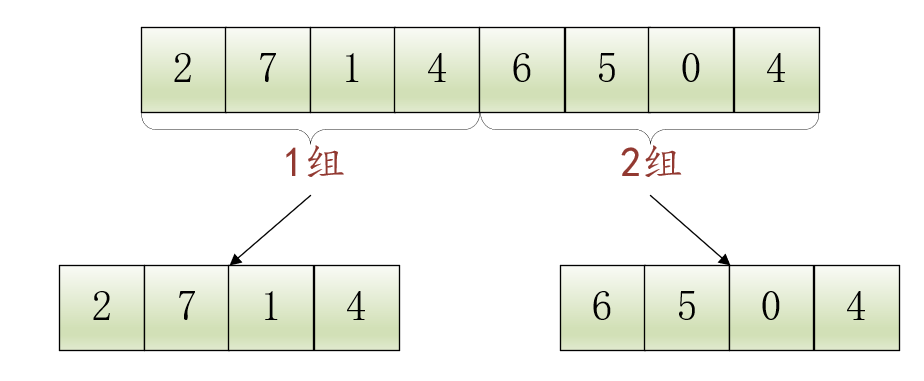
包含4个元素的数组还是太长了,继续将1组
和2组
分别拆分成2个组,现在就能得到4个组:1.1组
、1.2组
、2.1组
、2.2组
,每个组都包含2个元素:
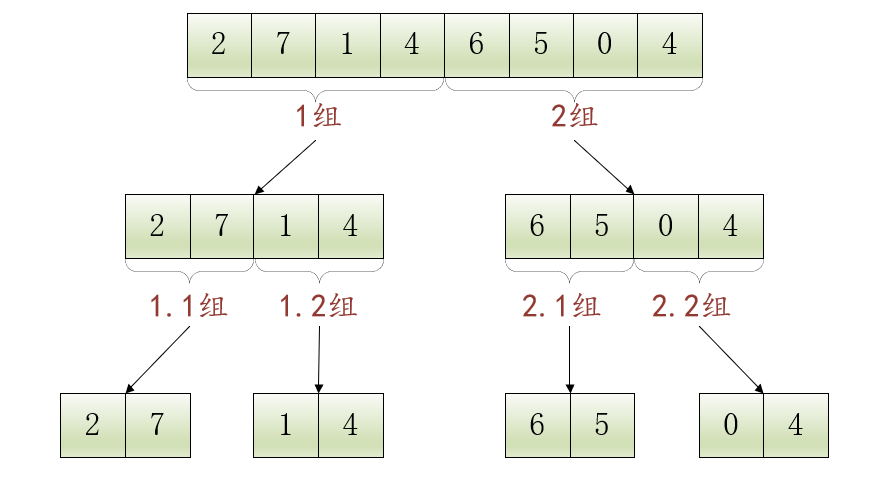
继续拆分包含2个元素的数组,将得到8个组:1.1.1组
、1.1.2组
、1.2.1组
、1.2.2组
、2.1.1组
、2.1.2组
、2.2.1组
、2.2.2组
,每个组只包含1个元素:
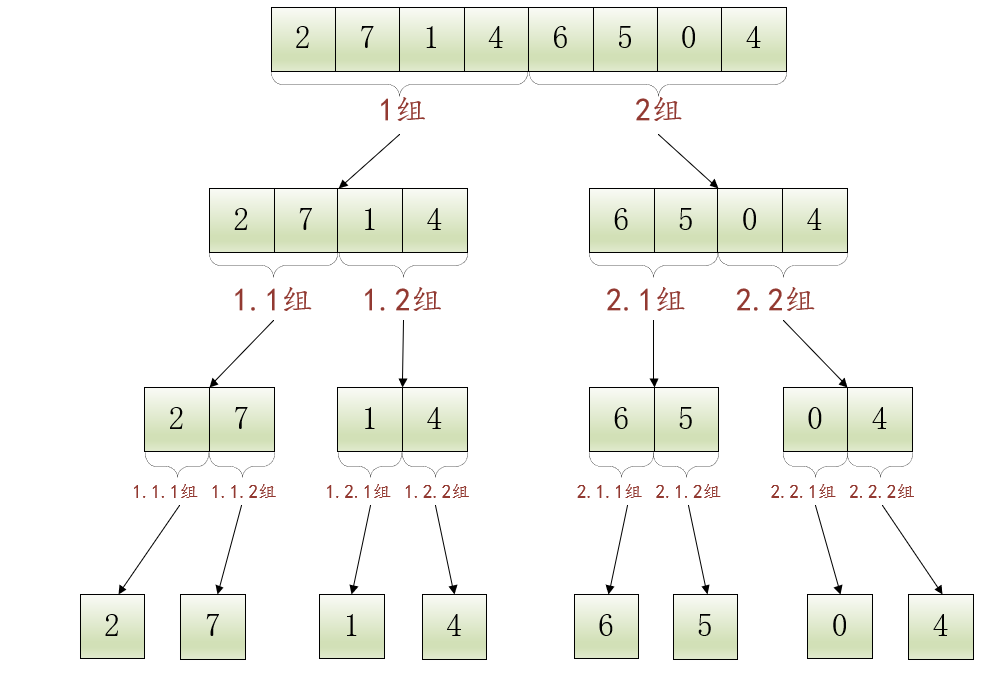
现在各个组仅包含1个元素,不能再拆分了,就可以对组中元素进行排序了。很显然,仅有1个元素的数组本身就是已经排好序的,也就是说:1.1.1组
、1.1.2组
、1.2.1组
、1.2.2组
、2.1.1组
、2.1.2组
、2.2.1组
、2.2.2组
这些仅包含1个元素的数组本身就是有序的,不用再额外进行排序了。
细节3
细节3
其实也很好解决,只要从头开始遍历两个子数组,每次都把两个子数组中较小的元素加入到最后的结果中即可。
比方说有两个包含2个元素的已排序数组[2, 7]和[1, 4],我们想把这两个数组合并为一个大的有序数组,那么我们可以定义两个变量i
和j
:
•i
表示第1个子数组的下标,初始指向第1个子数组的开头元素。
•j
表示第2个子数组的下标,初始指向第2个子数组的开头元素。
如下图所示:
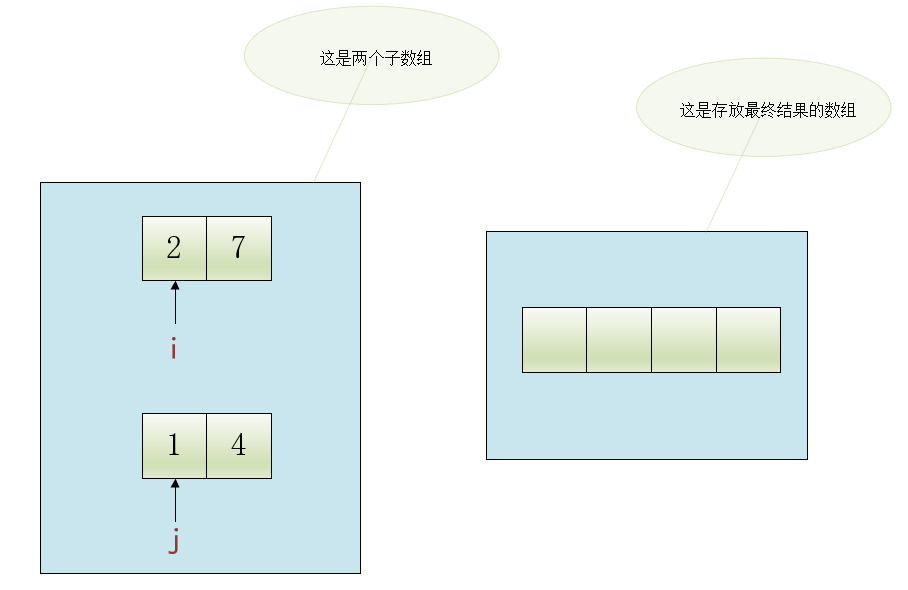
接着就可以依次向存放最终结果的数组中填入元素了:
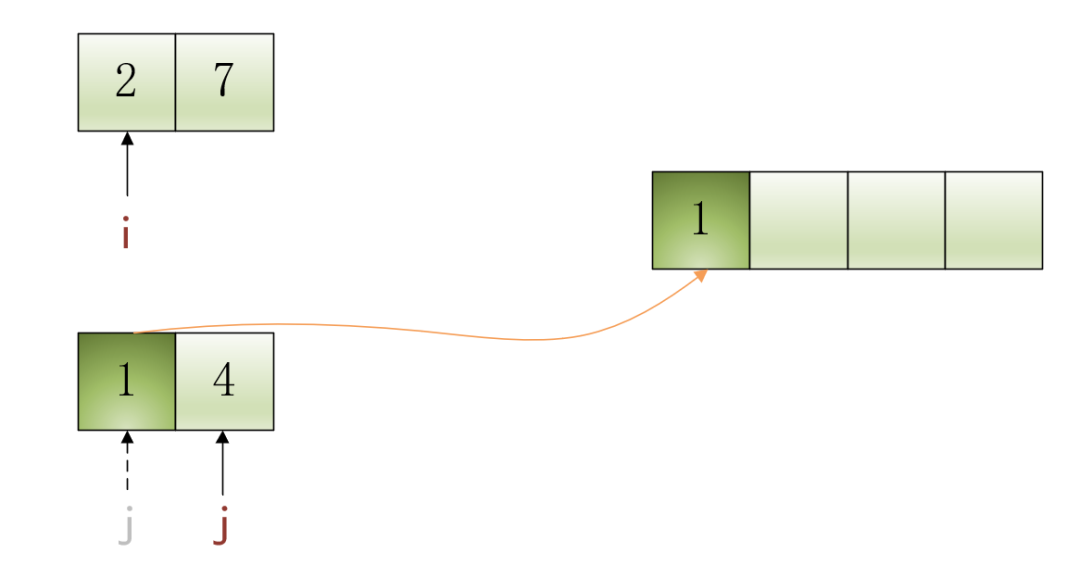
•第1步:当前i指向的元素是2,j指向的元素是1,比较i
和j
指向的元素哪个更小,由于2>1,所以将j指向的元素1填入结果数组中,并将j自增1,效果如下图所示:
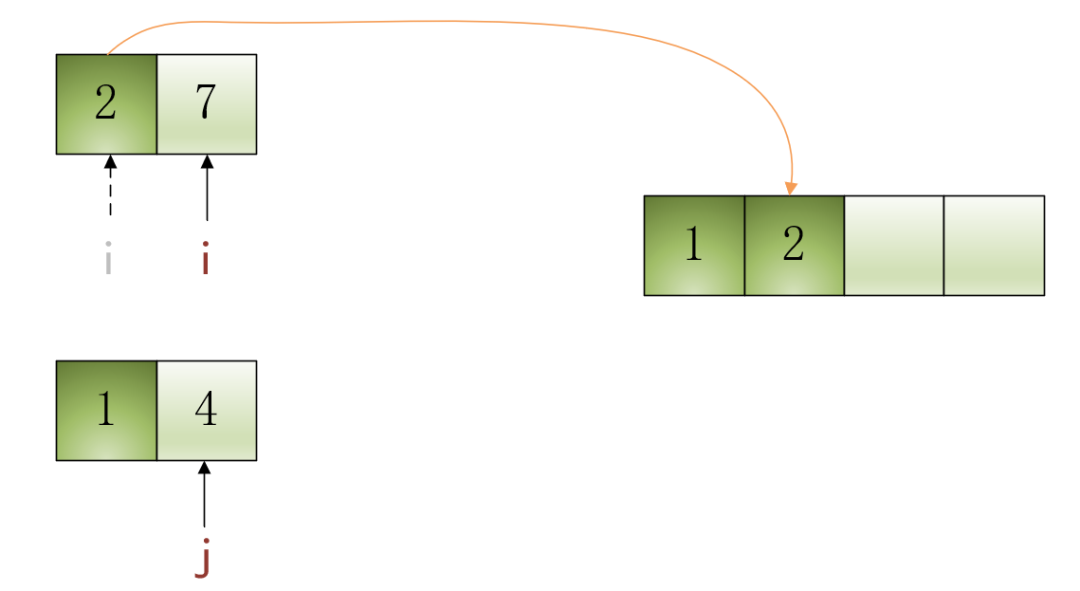
•第2步:当前i指向的元素是2,j指向的元素是4,比较i
和j
指向的元素哪个更小,由于2<4,所以将i指向的元素2填入结果数组中,并将i自增1,效果如下图所示:
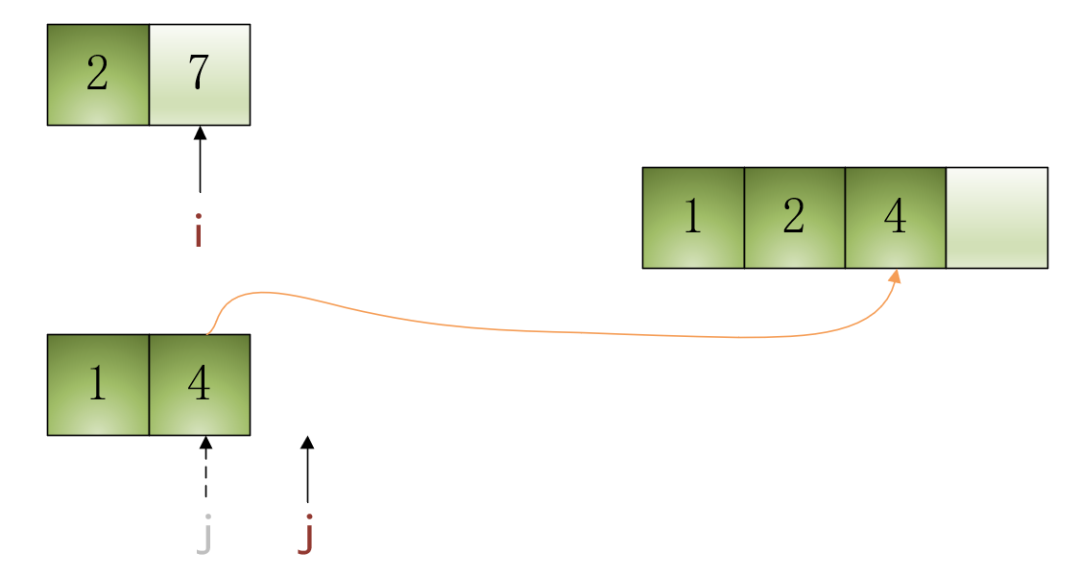
•第3步:当前i指向的元素是7,j指向的元素是4,比较i
和j
指向的元素哪个更小,由于7>4,所以将j指向的元素4填入结果数组中,并将j自增1,效果如下图所示:
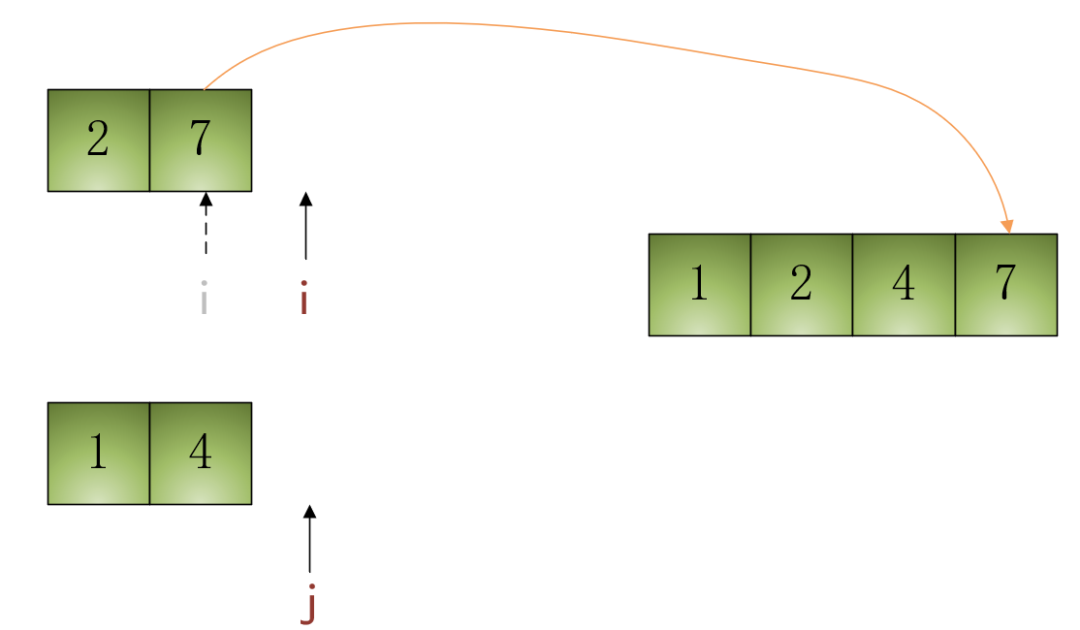
•第4步:当前i指向的元素是7,第2个子数组中的元素已经遍历完了,所以直接遍历第1个子数组即可,即将i指向的元素7填入结果数组收纳柜,并将i自增1,效果如下图所示:
知道了如何合并两个有序数组为一个大的有序数组之后,我们就可以完成子问题的合并
了。
继续看在处理细节2
时引入的例子:1.1.1组
、1.1.2组
、1.2.1组
、1.2.2组
、2.1.1组
、2.1.2组
、2.2.1组
、2.2.2组
中仅包含1个元素,相当于子问题已经得到解决,现在需要合并子问题了:
•将1.1.1组
、1.1.2组
中的有序数组合并,使1.1组
成为有序数组;
•将1.2.1组
、1.2.2组
中的有序数组合并,使1.2组
成为有序数组;
•将2.1.1组
、2.1.2组
中的有序数组合并,使2.1组
成为有序数组;
•将2.2.1组
、2.2.2组
中的有序数组合并,使2.2组
成为有序数组;
如下图所示:
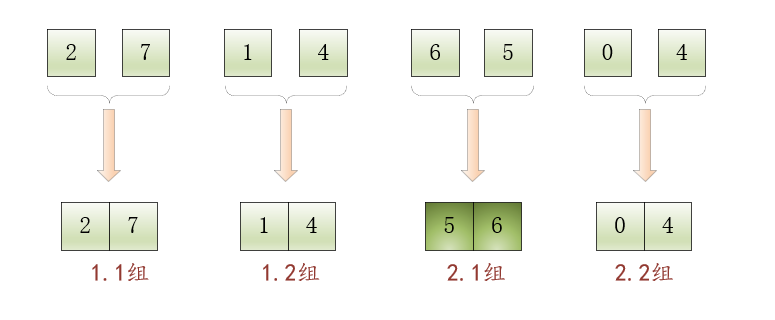
小贴士:
我们将2.1组的颜色加重,以表明组中的元素顺序进行了重排。
现在1.1组
、1.2组
、2.1组
、2.2组
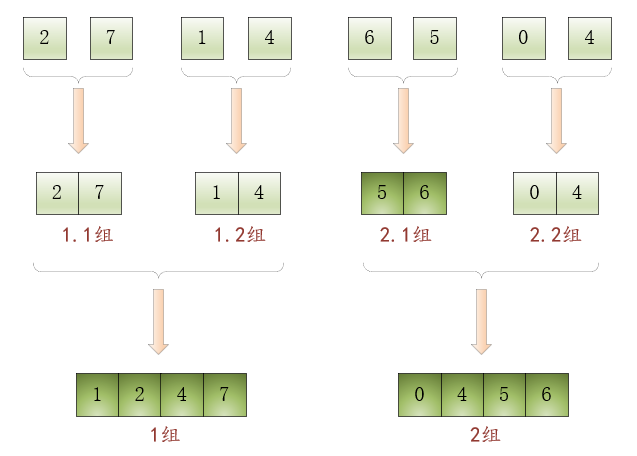
分别是4个有序数组,可以继续合并子问题:
•将1.1组
、1.2组
中的有序数组合并,使1组
成为有序数组;
•将2.1组
、2.2组
中的有序数组合并,使2组
成为有序数组;
如下图所示:
现在1组
和2组
分别是两个有序数组,可以继续合并子问题:
•将1组
和2组
中的有序数组合并为一个有序数组。如下图所示:
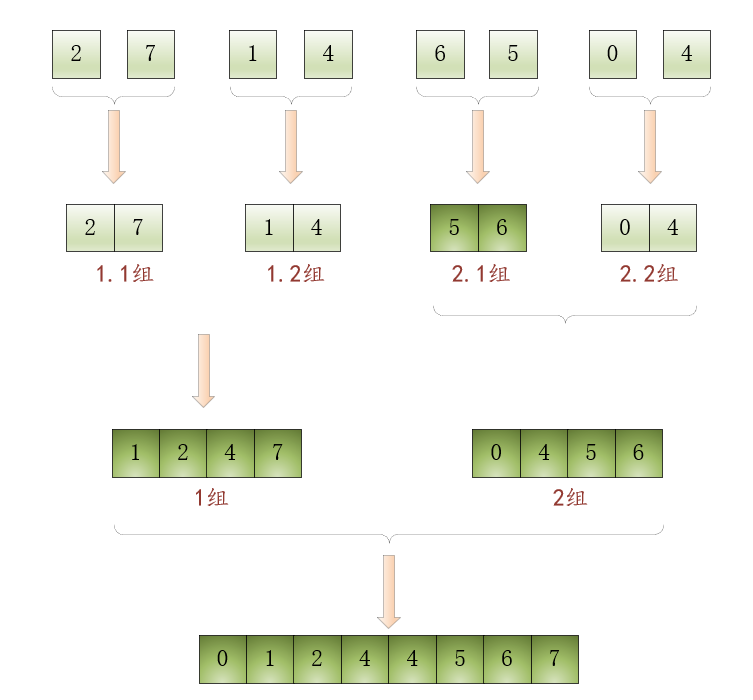
至此,最初排序包含8个元素的数组的原始问题就得到了解决!
好了,这个算法的流程就描述完了。相信绝大部分小伙伴还是可以轻松理解上述归并排序
的算法流程的,说起来也可以头头是道,但是一旦落实到笔上,就有点心有余而力不足的赶脚了,下面就来分析一下到底是哪里难住了我们~
Talk is cheap, show me the code
实现算法的语言并不是重点,我们下边将以Java为例,来看看如何写代码来实现归并排序
。
首先我们是要写一个用于排序的函数,就把它命名为mergeSort
吧,该函数用于对一个存储整数的int数组进行排序,我想100%的小伙伴能完成下面代码的编写:
public void mergeSort(int[] arr) {}
如果int数组arr中没有任何元素或者仅包含1个元素,那压根儿就不用排序了,我猜90%的同学可以把下述校验参数
的代码写出来:
public void mergeSort(int[] arr) {if (arr.length <= 1)return;}
小贴士:
校验参数十分重要,是展开后续过程的第一步,还是有很大一部分同学着急后续实现而忘记校验参数的。
下边到了真正精彩的地方了!
我们需要把数组分成两半,然后分别进行排序。这里出现了归并排序
的一个纠结点:
•纠结点
: 拆分出的子数组应该存储到哪里?
之所以说是一个纠结点
,是因为可以有2种实现思路:
•思路1
:为每个子数组都创建一个新的存储空间来存储它们。
•思路2
:还使用原数组保存子数组,使用额外的下标变量将其区分开即可。
很显然思路2
比思路1
更省存储空间,但思路1
可能更简单。我们接下来分别实现一下思路1
和思路2
。
思路1 如何实现
首先我们需要把原数组切成两半,然后创建两个新数组,并将原数组中对应的元素填入到新数组中,这个代码也并不难写,如下所示:
public void mergeSort(int[] arr) {if (arr.length <= 1)return;int mid = (0 + arr.length-1)/2;int[] a1 = new int[mid+1];int[] a2 = new int[arr.length-1-mid];copyArr(arr, 0, mid, a1);copyArr(arr, mid+1, arr.length-1, a2);}
首先我们需要计算中间元素的下标,用初始元素下标(例子中就是0)和末尾元素下标(例子中就是arr.length-1)的加和除以2即可得到中间元素的下标:
int mid = (0 + arr.length-1)/2;
然后创建两个数组a1
和a2
:
•a1
中存放原数组中下标0
到mid
的元素,共mid+1
个元素。•a2
中存放原数组中下标mid+1
到arr.length-1
的元素,共(arr.length-1) - (mid+1) + 1
,也就是arr.length-1-mid
个元素。
然后将原数组中下标0
到mid
的元素复制到新数组a1
中,将原数组中下标mid+1
到arr.length-1
的元素复制到新数组a2
中。copyArr
是我们自己创建的一个复制数组元素的工具方法(工具方法十分简单,就不多唠叨了):
/*** 将源数组中指定下标的元素复制到目标数组中* @param source 源数组* @param low 源数组初始下标* @param high 源数组末尾下标* @param dest 目标数组*/private void copyArr(int[] source, int low, int high, int[] dest) {for (int i=low; i <= high; i++) {dest[i-low] = source[i];}}
然后我们就应该:
•步骤1:给一个子数组进行排序;
•步骤2:给另一个子数组进行排序;
•步骤3:将步骤1和步骤2的得到的两个有序子数组合并为1个有序数组。
因为有3个步骤,所以我们需要定义3个函数,但由于步骤1
和步骤2
其实只是对某个数组进行排序,所以此时我们可以递归调用mergeSort
函数即可。
对于步骤3
,我们可以新定义一个merge
方法来完成将两个子数组合并为一个有序数组的功能,那么现在mergeSort
函数就变成了这样:
public void mergeSort(int[] arr) {if (arr.length <= 1)return;int mid = (arr.length-1)/2;int[] a1 = new int[mid+1];int[] a2 = new int[arr.length-1-mid];copyArr(arr, 0, mid, a1);copyArr(arr, mid+1, arr.length-1, a2);mergeSort(a1);mergeSort(a2);merge(a1, a2, arr);}
好了,现在mergeSort
函数就已经写完了,接下来就只需实现merge
方法即可。merge
方法用于将两个有序数组合并为一个有序数组,所以它的原型应该被定义为:
private void merge(int[] s1, int[] s2, int[] dest) {}
其中s1
和s2
是两个子数组,dest
是目标数组。
下边需要定义几个变量:
•i
表示第1个子数组的下标,初始指向第1个子数组的开头元素,也就是0。
•j
表示第2个子数组的下标,初始指向第2个子数组的开头元素,也就是0。
•pos
表示目前要填充目标数组哪个下标的元素,初始为0。
我们需要将目标数组填满,所以引入一个for循环,从目标数组开头元素开始,直到最后一个元素为止。代码如下所示:
private void merge(int[] s1, int[] s2, int[] dest) {int i = 0;int j = 0;for (int pos = 0; pos < dest.length; pos++) {这里写入填充内容}}
下边的任务就是填充for循环中的内容了,我们需要:
•比较s1[i]和s2[j]的大小:如果s1[i]较小,则把s1[i]填入dest[pos]中,并将i自增1;如果s2[j]较小,则把s2[j]填入dest[pos]中,并把j自增1。
那么代码就可以写成这样:
private void merge(int[] s1, int[] s2, int[] dest) {int i = 0;int j = 0;for (int pos = 0; pos < dest.length; pos++) {if (s1[i] <= s2[j]) {dest[pos] = s1[i++];} else {dest[pos] = s2[j++];}}}
上述代码忽略了一个最最重要的情况:如果s1先被遍历完,也就是i为s1.length时,接下来就不能访问s1[i]了,否则会抛出数组越界异常;如果s2先被遍历完,也就是j为s2.length时,接下来也不能访问s2[j]了,否则也会抛出数组越界异常。
忘记边界条件在编码实现算法时是极其容易出现,并且导致错误的问题。为简单起见,我们可以先考虑边界条件,然后再处理通用内容。在本例中,我们可以先处理一下s1遍历完以及s2遍历完的情况,然后再比较s1[i]和s2[j]的大小,如下所示:
private void merge(int[] s1, int[] s2, int[] dest) {int i = 0;int j = 0;for (int pos = 0; pos < dest.length; pos++) {如果s1已经遍历完,直接把s2[j]复制给dest[pos],并给j自增1if (i == s1.length){dest[pos] = s2[j++];}如果s2已经遍历完,直接把s1[i]复制给dest[pos],并给i自增1else if (j == s2.length) {dest[pos] = s1[i++];}以下是正常情况下的比较else if (s1[i] <= s2[j]) {dest[pos] = s1[i++];} else {dest[pos] = s2[j++];}}}
小贴士:
可以看到,增加判断边界条件的代码时,代码量会增大一倍甚至更多,我们之后可以介绍以下如何使用哨兵
来显著减少代码量。
这样,采用思路1
,也就是单独为子数组分配存储空间的方式实现归并排序
的过程我们唠叨完了,再来看一下采用思路2
如何实现。
思路2 如何实现
思路1
的弊病其实很明显,就是每次调用mergeSort
函数时,如果待排序数组中包含大于1个的元素,那就需要拆分成2个子数组,需要额外的为这两个子数组分配存储空间。
如果我们不想付出这些额外的成本,直接使用原数组来存储子数组,那么在对子数组进行排序时就不得不指定该子数组对应的起始下标和结束下标是什么,所以我们不得不再定义一个用于排序子数组的函数,我们可以把它称作mergeSort0
,该函数原型如下所示:
private void mergeSort0(int[] arr, int low, int high) {}
其中arr
是原始数组,low
指的是子数组的起始下标,high
指的是子数组的结束下标。
既然子数组的形式变成了原始数组+起始和结束下标
的形式,那相应的把两个有序子数组合并为一个有序数组的merge
函数的参数也需要变一下了。
我们在拆分某个数组为两个子数组时,是采用下边的方法进行拆分的:
•从数组开头的元素到中间元素属于一个子数组
•从中间元素的后一个元素开始,到数组最后一个元素属于另一个子数组
我们把被拆分数组开头元素的下标称作low
,把中间元素下标称作mid
,把末尾元素的下标称作high
,那么被拆分出来的子数组的下标范围就是:
•low
~ mid
属于一个子数组
•mid+1
~ high
属于一个子数组
在合并子数组时,我们只需要知道low、mid、high是多少即可知道这两个子数组的下标范围分别是多少,那么merge
函数的原型应该长这样:
private void merge(int[] arr, int low, int mid, int high) {}
有了给子数组排序的函数mergeSort0
和合并有序子数组的函数merge
,那我们就可以这样改写mergeSort
:
public void mergeSort(int[] arr) {if (arr.length <= 1)return;int mid = (arr.length-1)/2;mergeSort0(arr, 0, mid);mergeSort0(arr, mid+1, arr.length-1);merge(arr, 0, mid, arr.length-1);}
下边先来实现以下mergeSort0
,需要下边这些步骤:
•校验参数
•将待排序数组拆分成两个子数组
•先给1个子数组排序
•再给另一个子数组排序
•将两个已排序的子数组合并成一个有序数组
下边看一下具体的代码:
private void mergeSort0(int[] arr, int low, int high) {校验参数,如果数组包含元素个数不大于1,则不需排序if (low >= high)return;计算中间元素位置int mid = (low + high)/2;// 给一个子数组排序mergeSort0(arr, low, mid);// 给另一个子数组排序mergeSort0(arr, mid+1, high);// 将两个已排序子数组合并为一个有序数组merge(arr, low, mid, high);}
这样mergeSort0
就写完了,该看一下merge
函数如何编写了,不过这时候会有一个巨大的问题:子数组占用原数组的存储空间!
比方说某个数组有4个元素[2, 7, 1, 4],它的两个子数组都是有序的,分别是:[2, 7]和[1, 4],如下图所示:
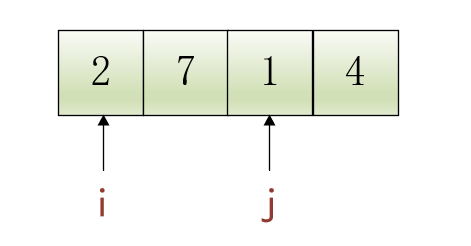
如果我们想对上图中的两个子数组进行合并,由于j指向的元素1
小于i指向的元素2
,所以会将1
放置在结果数组中的首个元素中,而结果数组就是原数组的话,直接就会把原数组的首个元素2
给覆盖掉!这是万万不能忍的。
为解决上述问题,我们需要一个临时的存储空间来存储有序子数组内容,这样在将结果写回原数组时才不会破坏子数组。这个临时的存储空间可以在merge函数内开辟,但是这样的话每调用一次merge函数都需要开辟一段临时的存储空间,也可以作为一个全局变量只申请一次存储空间。很显然后者优雅一些,我们这里采用后者。
首先我们定义一个名叫tmp
的成员变量:
private int[] tmp;
然后改写以下mergeSort
函数,给tmp
数组分配存储空间:
public void mergeSort(int[] arr) {//给全局变量tmp分配存储空间tmp = new int[arr.length];if (arr.length <= 1)return;int mid = (arr.length-1)/2;mergeSort0(arr, 0, mid);mergeSort0(arr, mid+1, arr.length-1);merge(arr, 0, mid, arr.length-1);}
然后我们在merge
函数里就可以使用这个tmp
数组了(由于在讨论思路1
的实现时已经详细讨论过merge函数的实现,所以我们这里就不花大篇幅讨论下边改版后的merge函数了):
private void merge(int arr[], int low, int mid, int high) {int i = low;int j = mid+1;//将子数组的内容先复制到tmp数组中for (int pos = low; pos <= high; pos++) {tmp[pos] = arr[pos];}for (int pos = low; pos <= high; pos++) {if (i == mid+1) {arr[pos] = tmp[j++];}else if (j == high + 1) {arr[pos] = tmp[i++];}else if (tmp[i] <= tmp[j]) {arr[pos] = tmp[i++];} else {arr[pos] = tmp[j++];}}}
好的,大功告成!
再回头看一下我们是不是还可以优化什么地方呢?
大家如果仔细观察一下mergeSort
和mergeSort0
两个函数的代码就会发现,它们的功能是极其类似的!只不过mergeSort
里指定的开始元素为恒定的0,结束元素为恒定的arr.length-1
,而mergeSort0
里用变量low
和high
来替代。当程序中出现了相同功能的代码时,一定要看一下能不能将功能相同的代码合并起来! 在本例中,mergeSort
中的代码起始和调用一次mergeSort0(arr, 0, arr.length-1)
是相同的,所以我们再精简一下mergeSort
函数:
public void mergeSort(int[] arr) {tmp = new int[arr.length];mergeSort0(arr, 0, arr.length-1);}
好的,这回才算大功告成了!
总结回顾
归并排序
算法极其简单,但它背后所体现的分治思想
却是那么的重要,我们下边再来梳理一下分治思想
,大概分为3步:
1.分(Divide):即将一个大问题拆分为若干个小问题(在归并排序
中就是将待排序数组拆分成2个子数组)。2.治(Conquer):使用递归的形式继续拆解小问题,直到问题小到可以很轻松的解决(在归并排序
中就是将子数组拆到只剩1个元素,那1个元素就肯定是有序的)。3.合(Combine):将已解决的子问题合并起来,从而解决大问题(在归并排序
中就是将已排序的子数组合并成一个有序数组)。
另外,在具体的归并排序
中,大家需要注意下述问题:
•进行参数校验十分必要
•在进行循环时注意边界条件的判断,可以先将特殊情况写清楚后,再写通用情况
•如何计算数组的中间元素以及如何划分子数组?选取(起始元素下标+结束元素下标)/2
的形式和直接用数组长度/2
有什么区别。
•如何存储子数组?是用额外的存储空间,还是在原数组中保存加上起始和结束下标呢?
•在遇到功能相同的代码时注意合并代码
小贴士:我们之前在讲MySQL的索引合并的时候用到了merge方法,大家还记得吗?。
好的,以上就是关于实现归并函数
时的一些思考,希望可以对大家有所帮助。
我们都是小青蛙,呱呱呱呱呱~
小青蛙历史文章
长按关注小青蛙,都是干货喔

原文链接为小孩子的《MySQL是怎样运行的:从根儿上理解MySQL》纸质书链接






