菜鸡每日一题系列打卡63天
每天一道算法题目
小伙伴们一起留言打卡
坚持就是胜利,我们一起努力!
题目描述(引自LeetCode)
一个机器人位于一个m x n网格的左上角(起始点在下图中标记为“Start”)。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
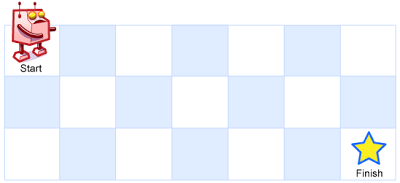
网格中的障碍物和空位置分别用1和0来表示。
说明:m和n的值均不超过100。
示例 1:输入:[[0,0,0],[0,1,0],[0,0,0]]输出: 2解释:3x3 网格的正中间有一个障碍物。从左上角到右下角一共有 2 条不同的路径:1. 向右 -> 向右 -> 向下 -> 向下2. 向下 -> 向下 -> 向右 -> 向右
题目分析
这道题目在上一道题目的基础上增加了障碍物的设置,但其实难度并未增加,思路还是一样的,采用动态规划的解法,只需要注意障碍物的处理即可。
思路尚不明确的小伙伴可以移步文末相关链接进行学习。话不多说,上代码!
代码实现
class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int[][] dp = obstacleGrid;int row = dp.length;int column = dp[0].length;// 无路可走if (dp[0][0] == 1) return 0;// 第一个网格dp[0][0] = 1;// 第一行for (int i = 1; i < row; i++) {if (dp[i][0] == 0 && dp[i - 1][0] == 1) dp[i][0] = 1;else dp[i][0] = 0;}// 第一列for (int i = 1; i < column; i++) {if (dp[0][i] == 0 && dp[0][i - 1] == 1) dp[0][i] = 1;else dp[0][i] = 0;}// 其他位置for (int i = 1; i < row; i++) {for (int j = 1; j < column; j++) {if (dp[i][j] == 0) dp[i][j] = dp[i - 1][j] + dp[i][j - 1];else dp[i][j] = 0;}}// 返回结果return dp[row - 1][column - 1];}}
代码分析
对代码进行分析,程序遍历了整个二维数组,因此,时间复杂度为O(mn),而就空间而言,仅仅使用了常数级别的额外空间,因此,空间复杂度为O(1)。
执行结果
相关链接

学习 | 工作 | 分享

👆长按关注“有理想的菜鸡”
文章转载自有理想的菜鸡,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






