AB测试,早已是数据工作者必须要掌握的一个知识点了。本文主要从AB测试实验设计者的角度,讲述了AB测试实验的定义、流程、原理;并简单介绍了AA测试、最优实验的选取以及最小样本量等知识点。
一、AB测试的一个简单定义
AB测试源于生物学中的对照实验,简单来说就是:对来自于同一用户总体的多个用户分组样本,每个组使用一个方案,在同一时间维度上去观察用户的反应并收集数据,最后根据假设检验结果评估出最好的方案,正式采用。
接下来,我会对以上定义进行逐句讲解说明,方便大家更加深刻的理解AB测试的概念:
同时性:分流和实验后续测试都应该是同时的。 同质性:要求最后分出的用户分组样本,在各个维度上的特征分布都较为相似,尽可能避免辛普森悖论发生。在日常实验中,我们常常使用的AAB测试,用于判断分组同质性。 唯一性:非重复抽样,要求用户不被重复计入同一实验中的多个组。
2. “每个组使用一个方案”,每一方案最好应遵循 单变量原则,便于归因。
这并不是说一个实验只能有一个影响因素,例如,APP开屏广告页的图片和文字分别有两种不同的设计,也就有4种组合,即4个方案。
3. “在同一时间维度上去观察用户的反应并收集数据”,用户的反应一般会体现在业务数据和用户体验数据上,实验设计者需要对主要影响指标有先验认知,并根据历史经验判断是否存在潜在的特征会影响到主要影响指标表现,实验中再观察用户分组样本的特征分布,避免辛普森悖论发生。
4. “最后根据假设检验的结果评估出最好的方案,正式采用”。在这一过程中,我们主要应用小概率事件原理,判断对应方案对我们所关注的核心指标是否有预期方向的显著影响,即根据假设检验的结果,判断哪些方案较原方案有统计意义上的显著差异。在多方案AB测试中,会根据 效应量 选出其中表现最好的版本。
二、AB测试实验流程
2.1 AB测试实验流程
在实际工作中,一个完整的AB测试流程可以分为四个步骤:
1、分析业务现状,提出优化方案,构建评估指标体系。
分析当前业务现状,确定最高优先级的改进点,提出优化方案。 设置主要指标来衡量方案的优劣;设置辅助指标来评估其他影响。
2. 设计方案原型、开发等准备工作。
3、AB实验设计:
明确目标群体:本次实验是否是面向特定群体的实验,是仅面向APP端还是Web端等等。 明确分流分层方案:
实验需要切分成多少组?一般情况下,会设置两组空白组进行AA测试,用于评估埋点、分流结果的合理性;在实验方案较少的情况下,每一方案也可以设置两组实验组,用来判断是否存在 heavy user 对实验结果产生影响。
如果存在能影响主要指标的特征,当前分流方案是否能够保证样本的随机和均匀分布,避免辛普森悖论发生。
确定最小样本量:给出检验功效(一般为0.8)、允许的极限误差大小(参考业务指标的波动大小),计算最小样本量。(计算推导详见第四部分) 确定实验时长: 结合目前日均活跃用户数,确定实验进行多少天能达到最小样本量; 根据实验目的和历史经验,考虑用户行为周期、适应期等其他影响因素对实验流量的干扰,适当延长实验时长,必要情况下,需要保证实验时长能覆盖一个最小周期。例如,在一个商务出行的实验场景中,存在工作日和周末用户行为的显著差异,最好保证实验时长在7天以上。
实验数据收集:实验数据一般AB实验平台或数仓同学会提供;在基建不完善的情况下,实验设计者还需要进行埋点等准备工作。 实验结果评估:如前所述,我们主要应用小概率事件原理,判断对应方案对我们所关注的核心指标是否有预期方向的显著影响,即根据假设检验的结果,判断哪些方案较原方案有统计意义上的显著差异。在多方案AB测试中,会根据效应量选出其中表现最好的版本。(假设检验原理详见第三部分) 给出实验结论:① 确定发布新版本;② 开放流量,继续测试;③ 优化方案重新实验;④ 放弃当前实验优化方向。
2.2 聊聊AA测试
在上文中,我们提到一般会设置两组空白组进行AA测试,用于评估埋点、分流结果的合理性。
当AA两组实验的指标差异很大时,一定是埋点、分流方法、数据统计中的一个存在问题或缺陷;在大公司,AB实验是通过AB实验平台完成,这些都不会存在较大问题。
AA测试还有一个重要作用是用于 评估AB实验的精度。这两组实验的主要业务指标均值的Gap称为系统误差;系统误差越小,说明AB测试的精度越高。一般情况下,AB实验结果中的业务指标的Gap至少需要大于AA中Gap的两倍,才认为AB实验结果具有统计显著性,否则可能只是正常误差。因为业务指标均值的波动率等于“总体方差/样本量”,所以,当Gap较大时,我们可以先尝试增加样本量。
2.3 聊聊A/B/N实验中最优方案的选取标准
当我们在同一实验中进行多组实验时,最后必然会面临最优方案的选择问题。如果各个实验组的样本量相差不大时,一个比较粗糙的做法是直接比较检验功效的大小,选出最优方案。
但是,当各个实验组的样本量存在较大差异时,或者我们想知道实验组和对照组的差异大小是否显著时,我们需要使用一些衡量效应量大小的指标帮助我们做出决定。一个常见的衡量效应大小的指标是 Cohen's d:

其中,Sw为实验组合对照组的合并标准差。
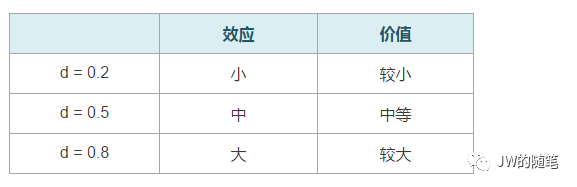
通常,评价效应量的标准如下表所示。若实验结果具有显著性,但效应量很小,也可以认为实验是不显著的。
三、AB测试实验原理
3.1 两个正态总体的抽样分布
对于AB实验的实验组和对照组,我们可以将实验数据的收集过程理解为一个随机抽样的过程。它们的样本均值是一个样本统计量,也是一个随机变量。在统计学中,我们将样本统计量的概率分布称为抽样分布;根据中心极限定理,我们就可以得到 样本均值的抽样分布:
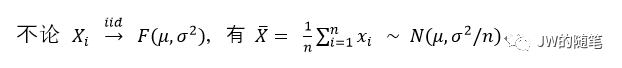
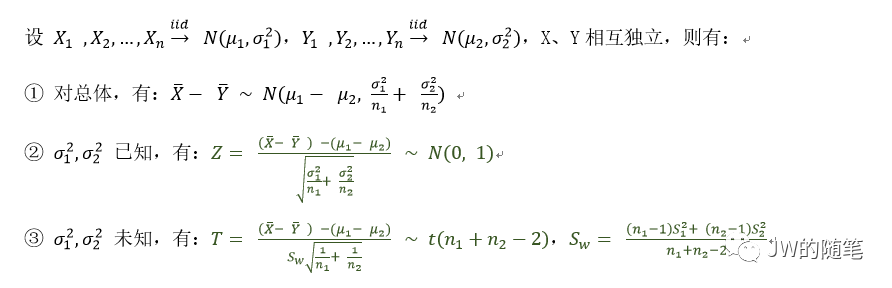
3.2 假设检验
得到了实验组均值和对照组均值的差的分布形式后,我们就可以进行假设检验了。顾名思义,假设检验分布两大步骤:
Step-1:假设 —— 给出原假设和备择假设
假设检验最终是根据小概率事件原则(相当于数学中的反证法),通过P值判定是否拒绝原假设。所以,我们将希望通过实验结果推翻的结论定为原假设。
Step-2:检验 —— 构造检验统计量,计算P值,做出决策
根据备择假设确定检验方向:备择假设含≠或=为双尾;含<或>则为单尾,其中,含<为左尾,含>为右尾。 确定显著性水平,一般取 0.05 或 0.01。
四、 最小样本量
4.1 为什么要计算最小样本量
首先,我们先来了解下假设检验中的两类错误:
弃真错误 α,等于显著性水平,表示原假设为真时拒绝原假设的概率;
纳伪错误 β,等于1-检验功效,表示原假设为假时接收原假设的概率。
流量供给有限:公司流量是有限的,而AB实验的流量需求往往远大于公司流量,流量分配的合理性会影响产品迭代速度。
试错成本大:比如,使用50%公司流量进行实验,使得GMV下降10%,损失惨重。
因此,计算使两类错误都处于较低水平的最小样本量,可以同时保证AB实验的精度和流量分配的合理性。
实际上,给出 显著性水平、两组样本均值的差异、检验功效、样本量 这四个指标中的任意三个都可以求出第四个指标的值。本文以两样本均值的单边检验为例,演示如何推导出最小样本量的计算公式。
两样本均值的单边检验
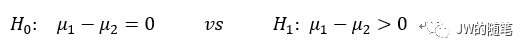
对于以上原假设和备择假设,令 d 为拒绝原假设时的两样本均值的临界差值,δ为假定的两样本均值差值,则有:
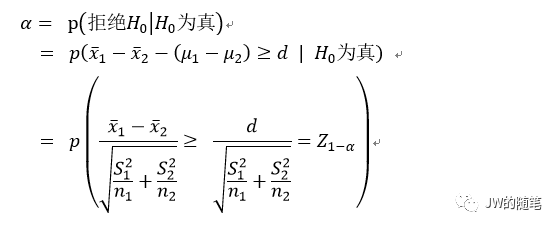
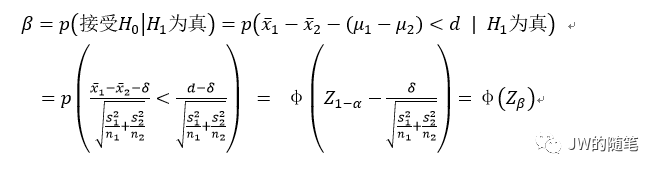
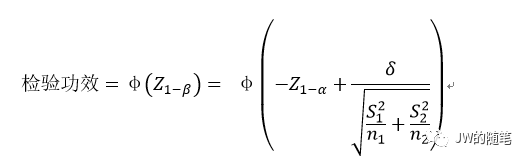
在实际分流中,实验组和对照组的样本量一般相差不大,所以,可假设 n=n1=n2,那么就有:
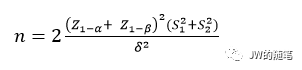
- 版权声明 -
文章版权属于本文作者
若有侵权,请联系本公众号删除或修改~
如有问题,欢迎留言~






