写在之前:此文为整理李江关于Power-Law的文章,已授权。
当我做NLP的时候,我曾经惊叹于Zipf’s law的神奇;后来写多了代码,发现80/20法则果然无处不在,80%的代码其实只是为了那20%的功能;当然,我也熟知长尾理论,它在今天的搜索引擎,电子商务中发挥着巨大的作用。而直到我开始做社交网络的数据分析,接触到一部分相关的理论,我才发现上述的这些理论/法则原来都是统一的,它们在数学上有个一致的定义,就是Power Law(冥律分布)。
什么是Power Law

这个函数,就是冥律分布的数学表达式。它其实是一种次方的关系。
特别关键的是,当k<1的时候,函数的图形如下:
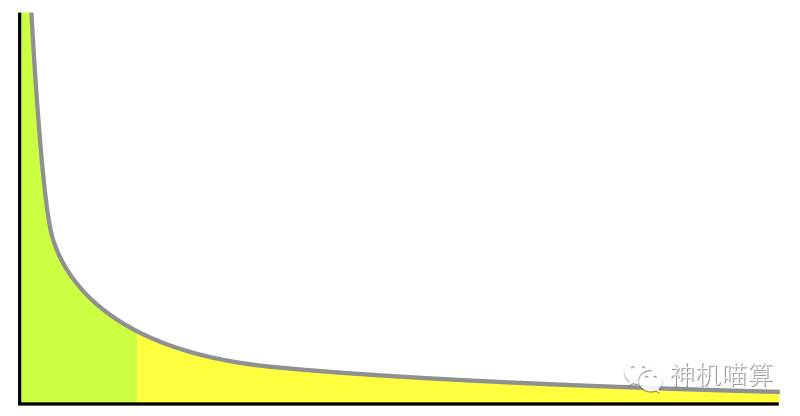
当x偏小的时候,微小的x的变化,会导致函数曲线发生巨大的变化。而在x轴的另一端,曲线缓缓的收敛到0。注意“缓缓”这个词非常的重要,我们后面再谈。
社交网络中的Power Law
power law在生活中无处不在,如果想了解更多的power law现象,可以看这里。本文只侧重于社交网络中的power law。
社交网络中最重要的一个冥律分布,是关于用户的好友数。如果将某个社交网络中所有人的好友数进行一个统计,那么这个统计符合冥律分布。抽象一些说,如果将社交网络看成一张图,那么图中每个节点的度数符合冥律分布。这是社交网络结构最重要的一个特性。目前几乎所有的社交网络都符合这一点(包括我自己实际观察到的)。
这个特性表示,网络中大多数节点的度数都很小,即好友数很少(分布图的左侧),但同时,有少量的节点,它们的度数可以非常的高(分布图的右侧)。
除此以外,如果网络中有内容,比如微博,那么对所有微博的转发量进行统计,它的分布也会满足power law。即大部分的微博转发量都会很小,可能大部分都小于10,甚至5。但是存在少量的热门内容,它们的转发量惊人的高。
为什么会是Power Law
想象一下,如果我们有很多的节点,随机的任取两个节点连接起来,最终形成了一个巨大的网络。这样随机构造的网络,它的节点度数的分布将是泊松分布(possion distribution):
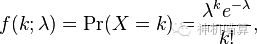

这个图意味着,在这个网络中,大部分节点的度数应该是处于中间的某一个值。度数过小或者度数过大的节点数都非常的少。
特别需要说明的是,泊松分布和冥律分布相比,虽然看上去,它们分布图的右侧都是收敛到0,但是,泊松分布的收敛速度非常快,很快就会趋近于0。而冥律分布相比要缓慢得多,这就是为什么我之前用“缓缓”这个词的原因。通俗解释,在泊松分布中,度数很大的节点几乎没有;而在冥律分布中,存在少量的度数很大的节点。
随机的思路走不通,换另一种方式构造网络:当网络中每添加一个新的节点的时候,这个节点更容易和当前度数高的节点连接。换句话说,网络中度数高的节点更容易“吸引”新的链接。
实验证明,这种方式得到的网络真正的符合Power Law。网络中大多数节点的度数都很低,但是有少部分节点,因为它们吸引链接的能力强,所以得到了越来越多的链接,而更多的链接导致它们的吸引力更强(富者更富),从而成为了分布图右侧的度数很高的超级节点,也称为中心节点。
所以,符合power law的社交网络并不是一个随机形成的网络。恰恰相反,虽然网络形成的过程会非常的复杂和多样,但却是在某种特定的法则(这种富者更富的现象也被称为Preferential attachment)约束下产生的。形成后的网络,少量但非常重要的中心节点支撑起了网络的框架,而在这框架下,是大量的度数少的普通节点。
所有节点度数分布符合power law的网络也被称为scale-free network,中文似乎翻译为“无尺度网络”。而由于这些中心节点的存在,会产生一个现象,就是scale-free network的网络直径一般都很小。换个通俗的名称,就是我们常说的“小世界”或者“六度空间”。我曾经计算过一个千万节点的社交网络的直径:随机的选择一些用户,看他们在几步内能够遍历到网络中99%的节点。最后,所有抽取用户的这个值都在5-8之间,而平均结果为5.99,和“六度空间”惊人的匹配。
其它
最近微博上有篇很有意思的文章:“研究Facebook会发现,平均一个用户有190个好友,而他们的朋友平均有635个好友。”,也就是说,你的好友的平均好友数会比你的好友数要高(有些绕口)。这事解释其实非常的简单,因为你(网络中的某个节点)一定会和几个网络中的中心节点相连接,而这些中心节点的好友数都是非常高的,这些值会将好友的平均好友数拔高,让你产生出这种错觉。
这反映一个更深层次的问题,就是在评价冥律分布的时候,不要采用平均值而应该采用中位数。在我研究的那个社交网络中,平均好友数能达到40+,而中位数只有14。
反思Power-Law
这段时间,一直都有个大大的问号困扰着我。我们总说,Power-Law无所不在,这也是Power-Law,那也是Power-Law,但是,我们是否有真正的去度量?还是仅仅凭着log-log plot上一条似是而非的直线,就认为满足Power-Law分布呢?
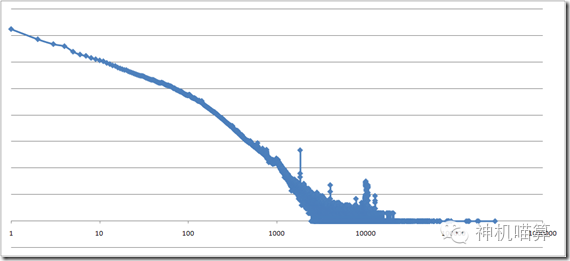
上图是一个真实Social Network的degree distribution。这样的曲线,我们好意思说它满足Power-Law吗?双log坐标的自身特性会将在坐标值很大区间内的抖动压缩得很不起眼,看起来平滑得像条直线,可是,真的有那么直吗?
我又找了一个看起来更漂亮的图(某paper上截取的):
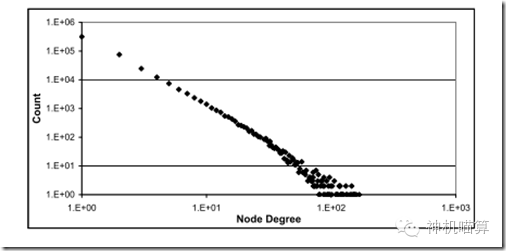
它应该更像是Power-Law,可是验证过了吗?谁去计算过α是多少?k是多少?如果用一个Power-Law曲线去拟合,误差有多大?除了Power-Law,是否可以找一个更复杂的曲线但能够更好的拟合呢?
我们现在常常将“长尾”,“二八法则”等同于Power-Law。但是,无论是“长尾”还是“二八法则”,其实都是比较模糊的性质,而满足这些性质的曲线有很多种,凭什么说都是Power-Law?
换个角度讲,Power-Law有那么重要吗?观察现实中的数据,很多都具有长尾特性,但知道这一点就够了。真的需要这些数据和Power-Law有完美的拟合吗?
最近看了一篇文章(点击“阅读原文”即可查看),里面的观点我大为赞同,不吐不快。以后还是少用Power-Law这个词,多用Long-Tail。
参考:
[1]: https://greatpowerlaw.wordpress.com/2012/09/23/why-power-law
[2]: https://en.wikipedia.org/wiki/Power_law
侠天,专注于大数据、机器学习和数学相关的内容,并有个人公众号:bigdata_ny分享相关技术文章。
若发现以上文章有任何不妥,请联系我。







