一直以来对float,double两个类型不甚了解,或者说一支半解,或者说百度所解.并且以前学习C语言的时候也是不懂! 并且MYSQL 这两个类型用得非常少,只是听说FLOAT,DOUBLE会丢失精度,反而DECIMAL不会丢失精度,存储金额字段的时候建议使用DECIMAL!
不过上姜老师的课时候,说DECIMAL会影响性能,因为它是变长类型,对于金额字段小数位给取消掉,使用乘法运算变成整数,用BIGINT来保存!
float 4字节 共32位 1 符号位 8 指数位 23 尾数位 精度是6-7位;
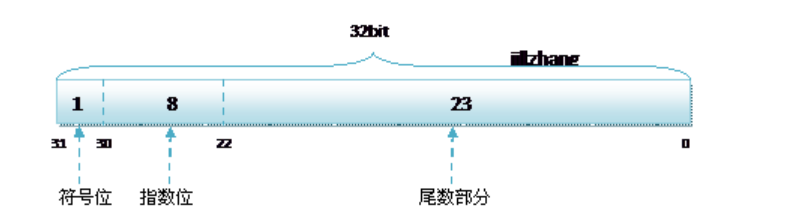
请注意,有效位数(精度)并不是指小数点后的位数,而是指表示数值的总有效数字位数。例如,数值123.456的有效位数为6位,而数值0.001234的有效位数为4位。
double 占8个字节,1bit(符号位) 11bits(指数位) 52bits(尾数位) 精度是15-16位;
float的指数范围为-127 至 +128,而double的指数范围为-1023 ~ +1024,并且指数位是按补码的形式来划分的。
这个补码我算不对,然后我问了CURSOR -CHATGPT3 实际上是指数+偏移量!
另外 float 和float(6,2) 没有任何差别只是显示效果有差别,这跟int和int(11)是一个道理.
float和double是固定字节,它们把数字先变成2进制,然后从整数最高位开始截取32和64位! 超过32位和64位就丢失了!
一个十进制转二进制人工算法
8.25
十进制的整数转换 ,成二进制比较简单,利用“除2取余倒记法”即可
8/2=4 余0
4/2=2 余0
2/2=1 余0
1/2=0 余1
倒序取余 1000
十进制的小数转换为二进制小数,主要是利用小数部分乘2,取整数部分,直至小数点后为0
0.25*2=0.5 =>0
0.5*2=1.0=>1
现在,我们将取得的数字从上到下写, 得到01即 0.01
8.25=1000.01
8.25二进制满足32位,不会被截取
科学计数法
整数部分保留一位整数,其余皆为小数.
1000.01 => 1.00001 *2^3 那么*2 表示底数,冥数; 且1位整数,3表示指数0.000101表示尾数.
如果是0.101 =>1.01 *2^-1
要保存进FLOAT里 1.00001 *2^3 还需要转换几下.

为了将数字8.25存入FLOAT类型字段里,我们需要将其转换为IEEE 754标准的32位单精度浮点数格式。以下是将8.25转换为二进制表示和科学计数法表示的过程:
1. 将8.25转换为二进制表示:整数部分为1000,小数部分为0.01(二进制)。所以,8.25的二进制表示为1000.01。
2. 将二进制表示转换为科学计数法表示:将1000.01表示为1.00001 * 2^3。
3. 确定符号位、指数位和尾数位:
- 符号位(1位):8.25是正数,所以符号位为0。
- 指数位(8位):指数为3,使用偏移表示法,即实际指数值等于存储值减去一个偏移值(对于32位单精度浮点数,偏移值为127)。所以,指数位的存储值为3 + 127 = 130,二进制表示为10000010。
- 尾数位(23位):尾数为1.00001,去掉隐含的第一个1,剩下的部分为00001000000000000000000。注意小数靠近小数点的在高位,
4. 将符号位、指数位和尾数位组合成32位单精度浮点数表示:
0 ,10000010 ,00001000000000000000000。
所以,当将数字8.25存入FLOAT类型字段时,实际存储的二进制表示为01000001000001000000000000000000。
下面是抠图过来的,尾数少个0,从最后一步倒看!

float丢失精度
假如我们有一张表,用来存储用户的积分,表定义如下:
CREATE TABLE `f` ( `f1` float(10,2) DEFAULT NULL) ENGINE=InnoDB DEFAULT CHARSET=utf-8
然后向这个表里插入131072.32的积分值,如下所示
mysql> insert into f value (131072.32);Query OK, 1 row affected (0.00 sec)
mysql> select * from f;
+-----------+
| f1 |
+-----------+
| 131072.31 |
+-----------+
131072.32二进制
整数: 0010 0000 0000 0000 0000 用
小数:
0.32*2=0.64=>0
0.64*2=1.28=>1
0.28*2=0.56=>0
0.56*2=1.12=>1
0.12*2=0.24=>0
0.24*2=0.48=>0
0.48*2=0.96=>0
......
0101000111101011100001010001111010111000010100011111… 这是一个无穷数
10 0000 0000 0000 0000.0101 0001 1110 1011100001010001111010111000010100011111
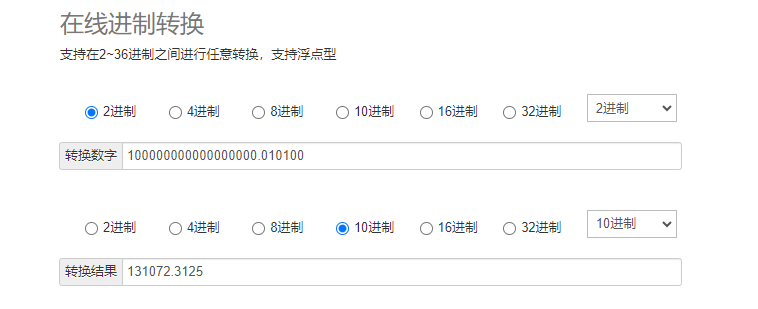
只能截取前32位进行存储
10 0000 0000 0000 0000.0101 0001 1110 10;
科学计数法
1.0000000000000000001010001111010*2^9
截取32位后再转换成10进制看样子如果四舍五入,float(10,2) 应该显示131072.32
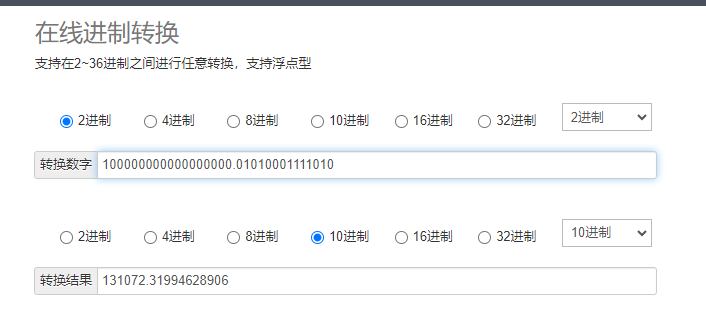
实际上我们修改表字段显示宽度float(10,3),float(10,6)
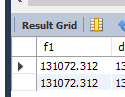
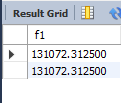
Why ?
我们把科学计数方法 转成FLOAT存储格式
1.0000000000000000001010001111010*2^9
第一位是 符号位 0 为正数
第2-8位是指数位 9+127 =136
第三部分是尾数 去1,存23为
1.0000000000000000001010001111010
0.00000000000000000010100;
感觉这尾数23位有丢失的可能,
1.0000000000000000001010*2^9
对照 (只能截取前32位进行存储)
10 0000 0000 0000 0000.0101 0001 1110 10;
那就是
10 0000 0000 0000 0000.0101 00;
真相大白了! 我们FLOAT 丢失精度 丢失了两次,
第一次 截取32位, 这个没有确定 我以为应该先转换成科学计数法再说.
不过如果遇到无穷小数,不截取怎么办?
第二次 就是尾数23位被截取了.尾巴超过23为的被丢弃了.
create table test(
t_float float,
t_double double
)
insert into test.test (t_float) values(123456);-- 正常
insert into test.test (t_float) values(1234567);-- 四设五入 1234570
insert into test.test (t_float) values(12345678901);-- 失真 12345700352
insert into test.test (t_float) values(12345.6); -- 正常
insert into test.test (t_float) values(12345.62); -- 四设五入 12345.6
insert into test.test (t_float) values(123.123); -- 正常
insert into test.test (t_float) values(12.1234); -- 正常
insert into test.test (t_float) values(1.12345); -- 正常
insert into test.test (t_float) values(1234.1234); -- 四设五入 1234.12
-- double
insert into test.test (t_double) values(1234567890123456);-- 正常
insert into test.test (t_double) values(12345678901234567);-- 四设五入 12345678901234568
insert into test.test (t_double) values(123.12345678901);-- 正常
insert into test.test (t_double) values(1234567890.123456);-- 正常
最后我们再长篇吹牛说下DECIMAL,DOUBLE跟FLOAT一样.
以下来之官方文档8.0
https://dev.mysql.com/doc/refman/8.0/en/precision-math-decimal-characteristics.html
数据类型为decimal的字段,可以存储的最大值/范围是多少?
DECIMAL列的声明语法为DECIMAL(M,D)。参数的值范围如下:
M是最大位数(精度)。它的范围为1到65。
D是小数点(小数位数)右边的位数。它的范围为0到30,并且不得大于M。
如果省略D,则默认值为0。如果省略M,则默认值为10。
也就是说D表示的是小数部分长度,(M-D)表示的是整数部分长度。
例如:decimal(5,2),则该字段可以存储-999.99~999.99,最大值为999.99。
decimal类型的数据存储形式是,将每9位十进制数存储为4个字节
| Leftover Digits | Number of Bytes |
|---|---|
| 0 | 0 |
| 1–2 | 1 |
| 3–4 | 2 |
| 5–6 | 3 |
| 7–9 | 4 |
上面意思说显示(5,2)它就能确保这么多,(5,2)不再是显示效果!
为了确保定义显示的范围,实际使用变长的格式存储,具体占用多少字节,看上面的表和算法.
decimal类型的数据存储形式是,将每9位十进制数存储为4个字节
999999999 => 00111011100110101100100111111111
正好4个字节32位!
算法大致如下
decimal(18,9),18-9=9,这样整数部分和小数部分都是9,那两边分别占用4个字节,共8个字节;
decimal(20,6),20-6=14,其中小数部分为6 就对应上表中的3个字节,而整数部分为14,14-9=5,就是4个字节再加上表中的3个字节 3+4+3=10个字节
decimal(10,2) 其中小数部分为2 就对应上表中的1个字节,而整数部分为8 对应是4个字节
网上流传的 DECIMAL(M,D) 占用字节是M+2 2表示小数位和符号位.
这是不实传说!
另外个谣传是 100存入 会变成字符串的"100" 存入占用3个字节.
最后个谣传是DECIMAL固定7个字节
DECIMAL最大占用多少字节应该是DECIMAL(65,0)
65/9*4=>7*4+1=29字节.
DECIMAL存储格式是?
CREATE TABLE `test_decimal` (
`TOTAL` decimal(20,6) DEFAULT NULL,
`MONERY` decimal(10,2) DEFAULT NULL,
`ID` int NOT NULL AUTO_INCREMENT,
PRIMARY KEY (`ID`)
) ENGINE=InnoDB AUTO_INCREMENT=3 DEFAULT CHARSET=utf8mb4 COLLATE=utf8mb4_0900_ai_ci
insert into dba.test_decimal (TOTAL,MONERY) VALUES(99999999999999.88,70000000.09);
insert into dba.test_decimal (TOTAL,MONERY) VALUES(-99999999999999.88,-70000000.09);
SELECT * FROM dba.test_decimal;
# TOTAL MONERY ID
99999999999999.880000 70000000.09 1
-99999999999999.880000 -70000000.09 2
它可以正确分辨出正负号
将 1234567890.1234 这个定点数分解为三部分:1、234567890、1234 ,每部分凑够9个数字,不够的就补0,
最后得到以下新的三部分:1、234567890、123400000。
根据基本原则和表格节约原则, 三个部分分别使用 1个字节,4个字节,2个字节
我们可以使用第三方网站在线进制转换,如 oschina.net 中的在线进制转换:
https://tool.oschina.net/hexconvert
由上面的结果,三个部分得到16进制:01, 0D FB 38 D2, 04 D2
也许二进制更亲切点,不过我们用GDB去跟踪原码时候16进制更常见.
这还不是最终的结果,还需要对最高位(01)进行反转。
如何反转呢?使用(1000,0000)和 我们最高位01 的二进制(0000,0001)进行异或运算,
0 + 0 = 0,0 + 1 = 1,1 + 0 = 1,1 + 1 = 0,
1000,0000
0000,0001
最终得到二进制数 10000001 ,转换为 十六进制 ,得到结果:81
最终结果是:81-0D-FB-38-D2-04-D2 。使用 1 + 4 + 2 = 7 个字节就实现了 1234567890.1234 的存储
如果是负数 -1234567890.1234 呢?
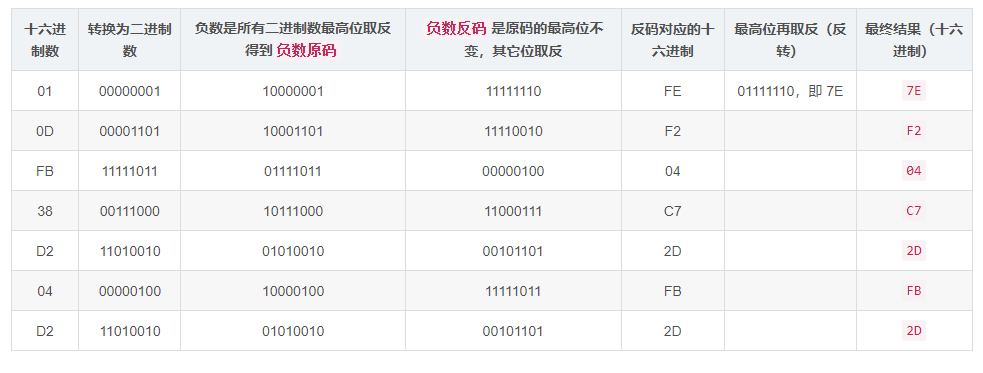
同样将负数 -1234567890.1234 分解为三个部分,先忽略前面的负号。由正数的处理过程,同样得到 01-0D-FB-38-D2-04-D2 7个十六进制数。
负数的反转稍微复杂,
第一步: 每一个字节单独反码 就是与(1000,0000)异或运算
这里是每一个字节16进制表达非常好 01是1个字字节,0D,FB,38分别也是1个节
第二步: 反码运算,每个字节最高位不变,其它位取反
第三步: 最高位的1个字节,就是8位 进行异或运算
负数 -1234567890.1234 的最终结果为:7E-F2-04-C7-2D-FB-2D
DECIMAL
columns do not store a leading +
character or -
character or leading 0
digits. If you insert +0003.1
into a DECIMAL(5,1)
column, it is stored as 3.1
. For negative numbers, a literal -
character is not stored.
官方这段话是说不存储符号+ -; 也不存储多余的0, 其实前后0都不要!
那么问题来了,存进去容易,读取出来怎么办?
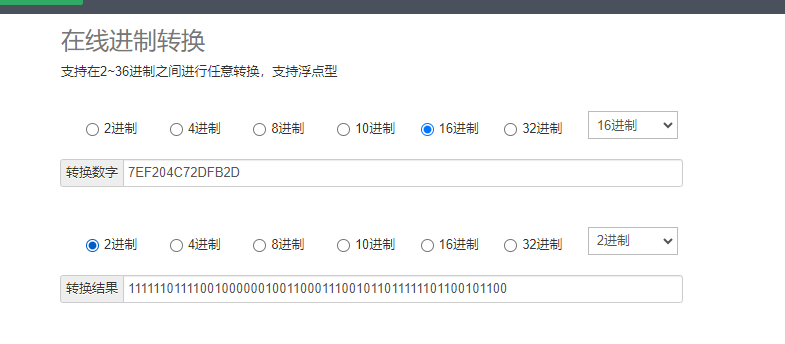
7E-F2-04-C7-2D-FB-2D
1111110111100100000010011000111001011011111101100101100
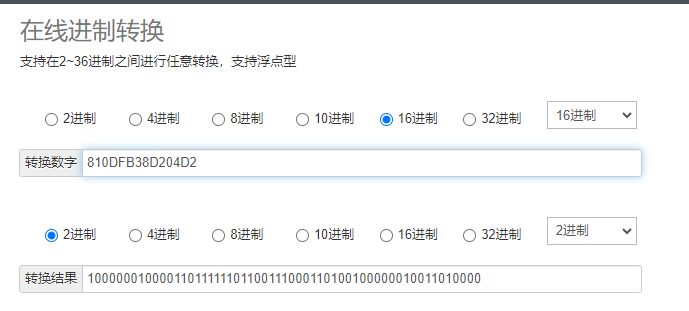
81-0D-FB-38-D2-04-D2
10000001000011011111101100111000110100100000010011010000
正负数高位都是1,说明确实没有报错符号位. 如何区分整数和小数部分呢?
依靠定义(M,D) 不靠谱,因为我们使用表节约原则.
那只好看源码,还好百度出源码文件
【MySQL-8.0.31源码中的 decimal.cc 文件中的 decimal2bin 方法核心代码】:
反函数自然是BIN2DECIMAL()
/*
Restores decimal from its binary fixed-length representation
SYNOPSIS
bin2decimal()
from - value to convert
to - result
precision/scale - see decimal_bin_size() below
keep_prec do not trim leading zeros
NOTE
see decimal2bin()
the buffer is assumed to be of the size decimal_bin_size(precision, scale)
If the keep_prec is true, the value will be read and returned as is,
without precision reduction. This is used to read DECIMAL values that
are to be indexed by multi-valued index.
RETURN VALUE
E_DEC_OK/E_DEC_TRUNCATED/E_DEC_OVERFLOW
*/
int bin2decimal(const uchar *from, decimal_t *to, int precision, int scale,
bool keep_prec)
{
int error = E_DEC_OK, intg = precision - scale, intg0 = intg / DIG_PER_DEC1,
frac0 = scale / DIG_PER_DEC1, intg0x = intg - intg0 * DIG_PER_DEC1,
frac0x = scale - frac0 * DIG_PER_DEC1, intg1 = intg0 + (intg0x > 0),
frac1 = frac0 + (frac0x > 0);
dec1 *buf = to->buf, mask = (*from & 0x80) ? 0 : -1;
const uchar *stop;
uchar *d_copy;
int bin_size = decimal_bin_size_inline(precision, scale);
sanity(to);
d_copy = (uchar *)my_alloca(bin_size);
memcpy(d_copy, from, bin_size);
d_copy[0] ^= 0x80;
from = d_copy;
FIX_INTG_FRAC_ERROR(to->len, intg1, frac1, error);
if (unlikely(error)) {
if (intg1 < intg0 + (intg0x > 0)) {
from += dig2bytes[intg0x] + sizeof(dec1) * (intg0 - intg1);
frac0 = frac0x = intg0x = 0;
intg0 = intg1;
} else {
frac0x = 0;
frac0 = frac1;
}
}
to->sign = (mask != 0);
to->intg = intg0 * DIG_PER_DEC1 + intg0x;
to->frac = frac0 * DIG_PER_DEC1 + frac0x;
if (intg0x) {
int i = dig2bytes[intg0x];
dec1 x = 0;
switch (i) {
case 1:
x = mi_sint1korr(from);
break;
case 2:
x = mi_sint2korr(from);
break;
case 3:
x = mi_sint3korr(from);
break;
case 4:
x = mi_sint4korr(from);
break;
default:
assert(0);
}
from += i;
*buf = x ^ mask;
if (((ulonglong)*buf) >= (ulonglong)powers10[intg0x + 1]) goto err;
if (buf > to->buf || *buf != 0 || keep_prec)
buf++;
else
to->intg -= intg0x;
}
for (stop = from + intg0 * sizeof(dec1); from < stop; from += sizeof(dec1)) {
assert(sizeof(dec1) == 4);
*buf = mi_sint4korr(from) ^ mask;
if (((uint32)*buf) > DIG_MAX) goto err;
if (buf > to->buf || *buf != 0 || keep_prec)
buf++;
else
to->intg -= DIG_PER_DEC1;
}
assert(to->intg >= 0);
for (stop = from + frac0 * sizeof(dec1); from < stop; from += sizeof(dec1)) {
assert(sizeof(dec1) == 4);
*buf = mi_sint4korr(from) ^ mask;
if (((uint32)*buf) > DIG_MAX) goto err;
buf++;
}
if (frac0x) {
int i = dig2bytes[frac0x];
dec1 x = 0;
switch (i) {
case 1:
x = mi_sint1korr(from);
break;
case 2:
x = mi_sint2korr(from);
break;
case 3:
x = mi_sint3korr(from);
break;
case 4:
x = mi_sint4korr(from);
break;
default:
assert(0);
}
*buf = (x ^ mask) * powers10[DIG_PER_DEC1 - frac0x];
if (((uint32)*buf) > DIG_MAX) goto err;
buf++;
}
/*
No digits? We have read the number zero, of unspecified precision.
Make it a proper zero, with non-zero precision.
Note: this is valid only if scale == 0, otherwise frac is always non-zero
*/
if (to->intg == 0 && to->frac == 0) decimal_make_zero(to);
return error;
err:
decimal_make_zero(to);
return (E_DEC_BAD_NUM);
}
源码大家自己看下,大概是麻烦的事情!