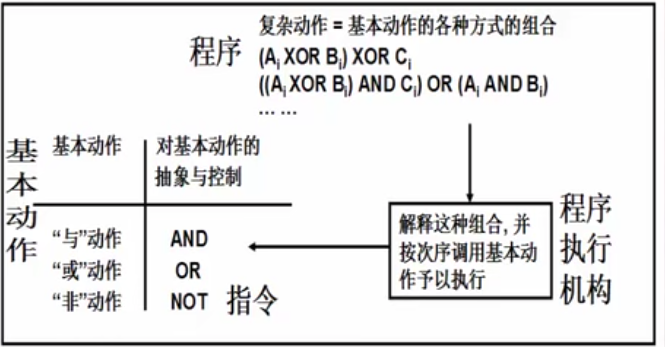
关系模型简述
关系模型是基于表的处理方式抽象形成的。是在对传统表及其操作进行数学化严格定义基础上,引入集合理论与逻辑学理论提出的。
关系模型也是数据库的三大经典数据模型之一,也是现在大多数商品化数据库系统所仍然再用的数据模型。数据库标准语言也是基于关系型数据库的。
形象地来说,一个关系(relation)就是一个Table。关系模型就是处理Table的,他由三个部分组成:
描述DB各种数据库的基本结构形式 描述Table与Table之间所可能发生的各种操作(关系运算) 描述这些操作所应遵循的约束条件(完整性约束)
研究关系模型就是研究如何描述Table,研究Table的操作的含义与结果、研究Table的各种约束。
“其实关系并不等同于Table,关系是一个数学概念,是一种集合。而Table是我们实际生活中的一个抽象,是一个实例。集合是不允许重复的,但是在实际生活中可能会出现两组完全一样的数据。
”
关系模型的三要素
基本结构
基本操作
集合运算符:∪:并(Union);∩:交(Intersection);—:差(Difference);×:广义积(ProDuct); 关系运算符:σ:选择(Selection);π:投影(Projection);⋈:连接(join);÷:除运算(Divsion);
完整性约束
实体完整性、参照完整性、用户自定义完整性
关系模型和关系数据库语言的关系
关系代数
元组演算
域演算
数学描述->用户使用的语言->开发软件
什么是关系?
严格定义一个表,我们先说明一些有关关系的重要概念
域(Domain)
域(Domain)
是数据库中列可能取的值的集合,例如性别的域就是{男,女},课程的域是{数据库系统,离散数学,Java程序设计语言,….}。
笛卡尔积
笛卡尔积(Cartesian product)
是元组及所有可能组合成的元组。从n个域中中可以取得所有的情况的集合就是笛卡尔积。
例如下面有两个域:
R1 = {小明,小红,小强}复制
R2 = {男, 女}复制
那么笛卡尔积就是
D = R1×R2。也就是下面这组元组
D = {(小明,男),(小明,女),
(小红,男), (小红,女),
(小强,男), (小强,女)}复制
容易看出来,笛卡尔积就是各个域中所有元素能够组成的元组的集合。
我们假设一个表中有三个域,每个域含有1000个元素。那么它们的笛卡尔积所组成的新集合会达到十亿个元素,实际应用中,这种集合是没有研究价值的。为了能够集合能够被研究,我们引入了关系的概念。
关系
一组域的笛卡尔积的子集。笛卡尔积中不是每一个组合都是有意义的,关系就是笛卡尔积中有意义的组合的集合。由于关系的不同列可能来自同一个域,为了区分,需要为每一列起一个属性名。
表示为:R(D1,D2,…,Dn)
R:关系名 n:关系的目或度
如上面的笛卡尔积,假设小红是女生,那么(小红,男)这个元组是无意义的。假设我们新添加一个配偶
的属性,这个配偶的属性的域是和最开始的那个名字的域一样的。为了区分,我们为最开始的属性取名为username,后面加入的取名为husband/wife。
下面是关系的描述:
R(A1:D1,A2:D2,…,An:Dn)A是属性名、D是域,n是度或目,元组的个数称为基数
在许多DBMS中,属性向域的映像直接说明为属性的类型、长度等。如varchar(10)。
关系的特性
列是同质。每一个列的分量来自同一域 不同的列可以来自同一个列,所以要有属性名 关系的任意两个元组不能完全相同。这是集合的要求。不过在实际应用中,表可能不遵从此特性,所以关系不一定完全等同于表 属性不可再分特性:又被称为关系第一范式。 分量必须取原子值
候选码/候选键
关系中的一个属性组,其值能唯一标识一个元组。从该属性组中去掉任何一个属性,他就不具有这一性质了。
🔺:有时关系中有很多组候选码。
主码(Primary)/主键
当有多个候选码时,可以选择一个候选码作为主键。DBMS以主码为主要线索管理关系中的各个元组.
主属性/非主属性
包含在任何一个候选码中的属性被称作主属性,而其他属性被称作非主属性.
最简单的情况:候选码只包含一个属性
最极端的情况:所有属性构成这个关系的候选码,称为全码
外码/外键
关系R中的一个属性组,它不是R的候选码,但他与另一个关系S的候选码相对应,这个属性组被称为R的外码
三类关系
基本关系(基本表或基表):实际存在的表,是实际存储数据的逻辑表示 查询表:查询结果对应的表 视图表:由基本表或其他视图表导出的表,是虚表,不对应实际存储的数据。
关系模式
关系模式是型,关系是值。关系模式是对关系的描述。
关系模式表示为:R(U,D,DOM,F)
R:关系名 U:组成该关系的属性名 D:U中属性所来自的域 DOM:属性向域的映像集合 F:属性间数据依赖关系的集合
关系的完整性约束规则
实体完整性
关系的主码中的属性值不能为空值(不知道或无意义的值),因为主码具有唯一性,空值无法保证这一要求
“空值不参与算术、比较和逻辑运算。用来表现暂时不详的信息。一般有运算需求的属性组中会用默认值来代替暂时不知道的信息
”
参照完整性
如果关系R1的外码Fk域关系R2的主码Pk相对应,则R1中的每一个元组的Fk值要么等于R2中某个元组的Fk值,要么为空值,不允许出现R2中没有的值。
用户自定义完整性
用户针对具体的应用环境定义的完整性约束条件。如约束字符个数,数字范围等等。
DBMS在更新操作发生时,会按照用户定义的约束检查语句是否符合要求。达到用户自定义完整性。
关系代数介绍
基于集合,提供了一系列关系代数操作,如:并、差、笛卡尔积(广义积)、选择、投影等基本操作,以及交、连接和关系除等扩展操作,关系代数是基于集合思维的一种操作语言。
关系代数是一种抽象的语言,是学习其他数据库语言(如SQL)的基础。
关系代数操作
为什么需要关系代数
在计算机底层都是与或非等简单的操作,我们程序中的所有复杂操作到底层都需要拆解成这些简单的指令。
对于数据库来说也是如此,我们复杂的功能都需要拆解成简单的操作。这些简单的操作在关系型数据库中被称为关系代数操作,数据库管理系统将复杂的数据库语言转化为关系代数就不可避免地需要对关系代数的研究。
基本操作
集合操作:∪:并(Union);∩:交(Intersection);—:差(Difference);×:广义积(ProDuct);
纯关系操作:σ:选择(Selection);π:投影(Projection);⋈:连接(join);÷:除运算(Divsion);
并相容性
一些关系代数操作,如并、差、交等,需要满足“并相容性
”。即要求参与运算的两个关系及其相关属性之间有一定的对应性、可比性或意义关联性。
定义:关系R与关系S存在相容性,当且仅当:
关系R和关系S的属性数目必须相同; 对于任意i,关系R的第i个属性的域必须和关系S的第i个属性的域必须相同
这是进行并操作等操作的前提!
集合运算
并(Union)
定义:假设关系R和关系S是并相容的,则关系R和关系S的并运算结果也是一个关系,记作:R∪S,它由出现在关系R中,或者S中的元组构成。
数学描述:
形象来说:并运算就是将两个关系的元组合并成一个关系,在合并时去掉重复的元组。
差(Difference)
定义:假设关系R和关系S是并相容的,则关系R与关系S的差运算结果也是一个关系,记作:R-S。它由出现在关系R中但不出现在关系S中的元组组成。
数学描述:
广义笛卡尔积
定义:关系R和关系S的广义笛卡尔积由关系R和关系S的元组所有可能的元组的集合组成
笛卡尔集是后面所有连接运算的基础
笛卡尔积操作:
R×S=S×R 假设两个关系R和S,它们的元组个数分别为x和y(关系R的基数x,S的基数y)。R和S的笛卡尔积的元组个数是:x*y
关系运算
选择操作(Select)
定义:给定一个关系R,同时给定一个选择的条件Condition(简记con),选择操作的结果也是一个关系,记作:
条件con由逻辑运算符连接比较表达式组成
投影(Project)
一个关系的投影也是一个关系,记作。从关系R中选出属性包含在A中的列构成。
关系S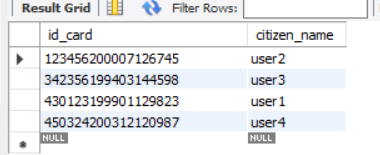 关系R
关系R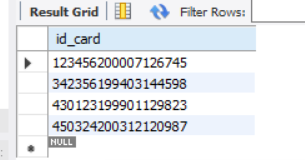
如上:关系R就是关系S中对id_card
这个属性的投影
连接运算(join)
自然连接
对于关系R与关系S自然连接是写为 (R ⋈S)的二元运算。自然连接的结果是在R和S中的在它们的公共属性名字上相等的所有元组的组合。
这里引用维基百科的一张表: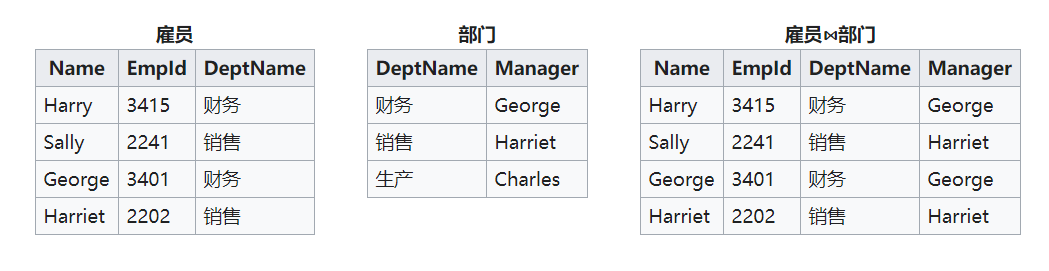
可以看到自然连接相当于将两张表按照名字相同的一列连接起来。
相关概念: