图1、图2和图3展示了二维空间向量A和B相交、正交和重合的情况。
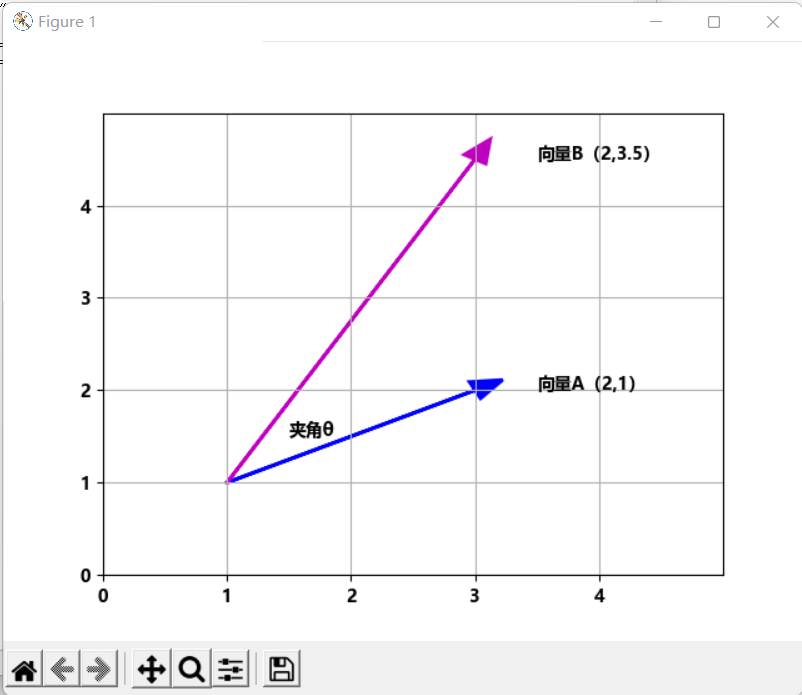
图 1向量A和B
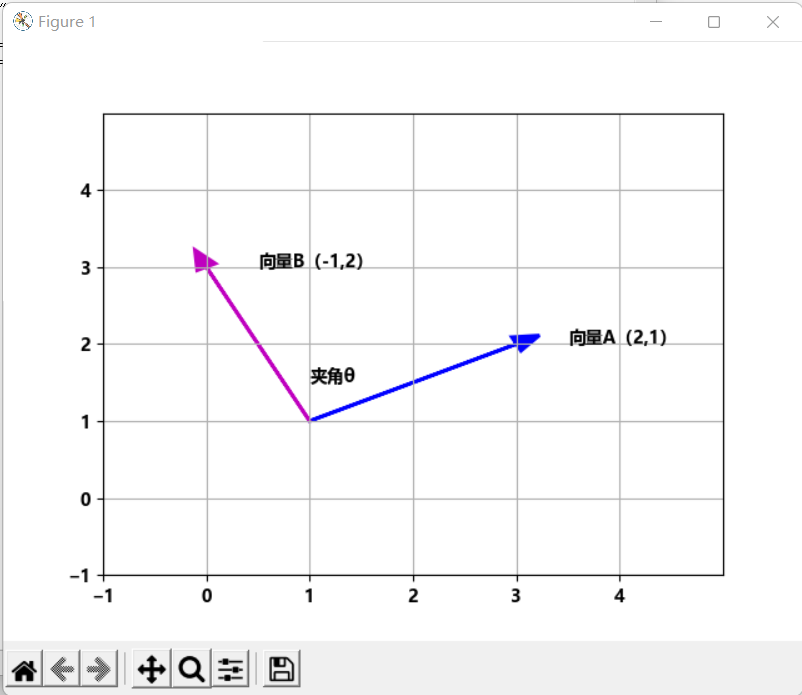
图 2向量A和B正交

图 3向量A和B重合
绘图代码【Python】
import numpy as npimport matplotlib.pyplot as pltplt.rc("font",family='MicroSoft YaHei',weight="bold")# 定义向量A和BA = np.array([2,1])B = np.array([2,3.5])# 创建坐标轴ax = plt.axes()# (1,1)为起点,绘制向量A和Bax.arrow(1, 1, *A, color='b', linewidth=2.0, head_width=0.20, head_length=0.25)ax.arrow(1, 1, *B, color='m', linewidth=2.0, head_width=0.20, head_length=0.25)# 设置X轴范围plt.xlim(0,5)# 设置X轴刻度major_xticks = np.arange(0, 5)ax.set_xticks(major_xticks)# 设置Y轴范围plt.ylim(0, 5)# 设置Y轴刻度major_yticks = np.arange(0,5)ax.set_yticks(major_yticks)# 绘制网格线plt.grid(b=True, which='major')# 绘制标注ax.text(A[0]+1.5,A[1]+1,"向量A(2,1)")ax.text(B[0]+1.5,B[1]+1,"向量B(2,3.5)")ax.text(1.5,1.5,"夹角θ")# 显示图像plt.show()
在二维空间内,A和B两个向量相交情况可以由夹角θ确定:若θ等于90度,向量A和B垂直,也称为向量A和B正交;若θ等于0度,向量A和B重合且方向相同;若θ等于180度,向量A和B在一条直线上,且方向相反;若θ大于0度,且小于180度,且不等于90度,向量A和B相交。可见向量A和B正交是相交的一种特殊情况。
向量的相交情况可以推广到n维空间,在n维空间内,任意两个向量A和B都成立。

上图画出了空间中相互垂直的两个向量,给出了一个直角边长分别为||A||和||B||,斜边长为||A+B||的直角三角形。由于向量A和B相互垂直,应用勾股定理可知:
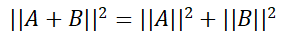
下面推导||A+B||^2公式:
||A+B||^2=(A+B)*(A+B)=A*A+2A*B+B*B=||A||^2+||B||^2+2A*B
上面推导的公式对n维空间任意两个向量A和B都成立
比较上面的两个公式,可得出A*B=0,即两个相互垂直的向量的点积为零。下面给出向量正交的定义:
对n维空间上两个向量A和B,当A*B=0时,称它们互相垂直或正交。
文章转载自数学遇上机器学习,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






