点击蓝字关注我们
应用之道
存乎一心

《认识支持向量机》系列推文将要带大家了解什么是高端大气的支持向量机(SVM)。阅读本系列推文需要具备一定的线性代数和高等数学基础,如果实在没有……那也没有关系,欢迎吃瓜群众搬起小板凳围观。
本系列推文共有三篇,主要内容分配如下:
(一)认识支持向量机
(二)线性可分支持向量机、线性支持向量机
(三)非线性支持向量机
本系列推文参考资料如下:
(一)台大 李宏毅 《机器学习》
(二)新加坡 王圣元 《王的机器》
(三)华为 李航 《统计学习方法》
(四)美国 Richard O. Duda等 《模式分类》
(五)其它互联网资料
本文中如有错误,欢迎大佬们指正!
前言
本文作为「自然语言处理」专栏中基础推文之一,其主题选取了机器学习(Machine Learning)中极为重要的概念——支持向量机。支持向量机算是一个非常优雅的算法,它具有完善的数学理论,虽然如今工业界用到的不多,但它的意义依然非常大。本专栏没有也不太可能会按照传统课程的顺序从“损失函数”讲解到“神经网络”(毕竟我们都经历过背单词从Abandon背到Abandon的尴尬= =),本专栏仅选取与自然语言处理密切相关的Part。同时,小编默认大家对ML有一定的了解,无基础的同学可以自行查找资料补课哦(墙裂推荐台大李宏毅教授的相关课程)。
01
初识 SVM
支持向量机(个人觉得译作支撑向量机更合理)即 Support Vector Machine,简称 SVM 。当我最开始听到这个名词时,一种莫名的神秘感油然而生,似乎把 Support 这么个具体的动作和 Vector 这么个抽象的概念拼到一起,然后再做成一个 Machine ,听起来无比的高大上!
实际上支持向量机只是一种算法,确切的说是一种广义线性二分类算法,通过引入核函数它也进行非线性分类。它的基本思想是在特征空间中寻找间隔最大的分离超平面使数据得到高效的二分类。相当多的人认为支持向量机是“效果最好的现成可用的分类算法”之一,它曾经推动了机器学习的发展。因此了解支持向量机是学习机器学习过程中非常重要的一个环节。
既然SVM是一种分类算法,那与其它分类算法(如线性回归等)有何不同?我们为什么需要它?
存在必定合乎理性,别急,我们慢慢来看……
我们将两组数据分别用“红”与“蓝”两种不同的颜色表示,用三个特定的样例引导大家走进支持向量机的大门。
样例一:红色与蓝色图标线性可分
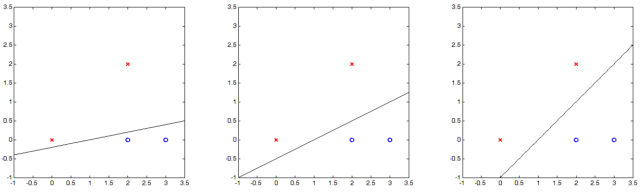
假设上面三张图的分隔线都分类正确,请问你觉得哪一条效果最好?我相信大部分人的直觉会告诉他“第三条分割线效果最好”,事实确实如此,且听如下分解:
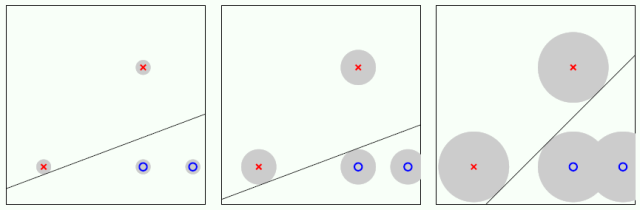
解释 1:实践中数据都有测量误差,如下图灰色圆圈所示,圆圈的半径代表误差的数量,也就是说测量的点可以在灰色圆圈内任何位置出现。因此,一个好的分隔线可以在容许误差的情况下还分类正确,能容忍越多误差该分隔线越好,显然第三幅图的分隔线最好。
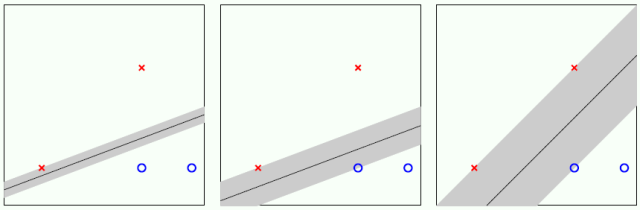
解释2:我们还可以从分隔线角度来描述误差容忍度,如下图分隔线旁边灰色缓冲带。我们不允许缓冲带里面有数据点,为了得到最宽的缓冲带,可以从那个分隔线两边往外延伸直到碰到一个数据点,这些数据点称为支持向量(Support Vector)。这个最宽的缓冲带反映了这个分隔线容忍误差的程度,其专业术语叫做间隔 (Margin)。我们要做的就是最大化这个间隔。
样例二:红色与蓝色图标轻度线性不可分
如下图所示,左图中同样有红与蓝两组数据,但与样例一不同的是:我们无法在平面上找到这样一条直线将两组数据“完美”的分开。
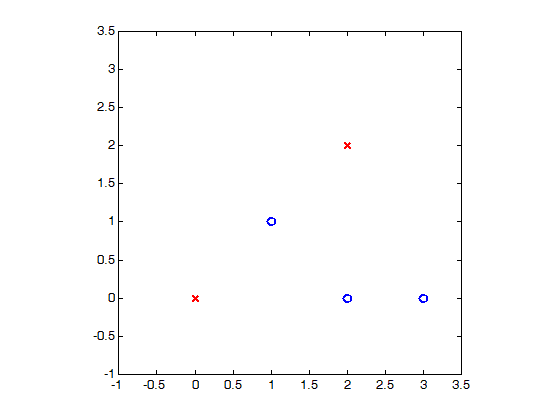
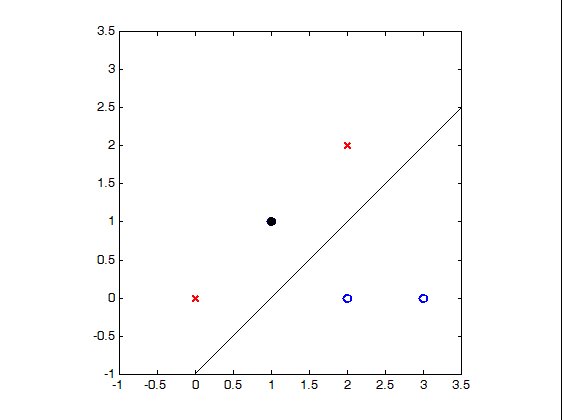
如果我们做出些许妥协——牺牲精度,就能找到一条“勉强”满足需求的直线。比如,我们允许 (1, 1) 这个蓝圈分类错误,在图中我们将它标记为黑色。如果说样例一中所有红叉和蓝圈“完美”分隔的情况叫做硬分隔 (Hard-Margin),样例二里面允许错误的“勉强”分隔叫做软分隔 (Soft-Margin)。
样例三:红色与蓝色图标重度线性不可分
假设红色图标全部被蓝色图标包围,很明显在平面上我们连一条“勉强”可分的直线都找不到,那么该怎么办呢?换句话讲,该问题线性不可分,如何将它转化成线性可分?

简单,上面的点在二维平面线性不可分,我们把它转换成三维空间使得它们线性可分。第一步,我们生成新的特征Z=X^2+Y^2,将平面上的点映射到三维空间:
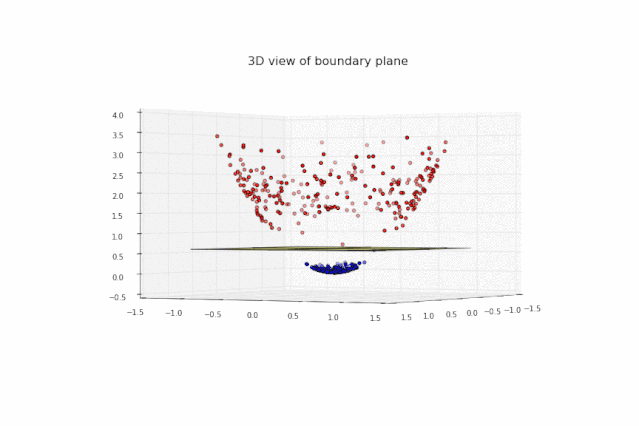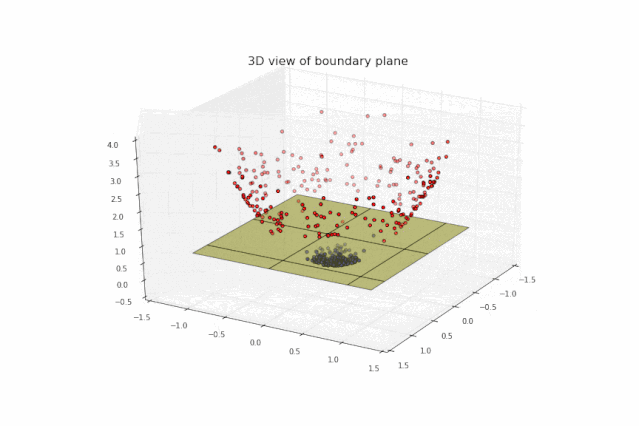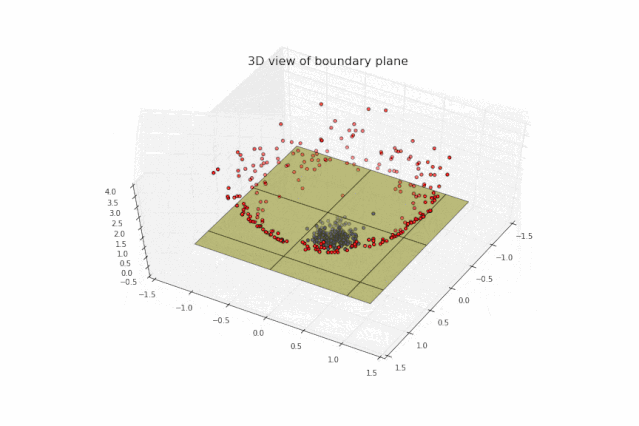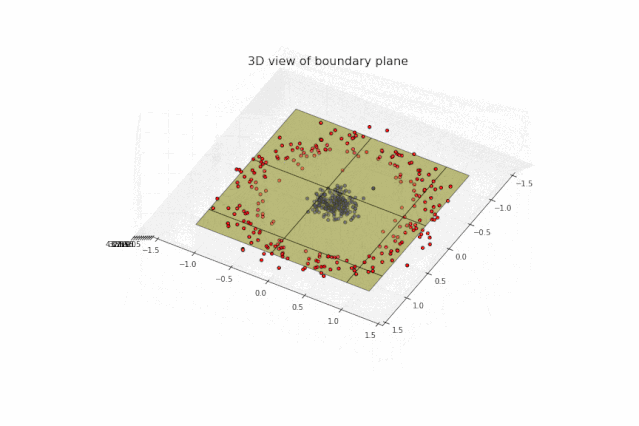
很明显这些点在三维空间上线性可分。第二步,我们寻找类似下图的绿色分隔平面:
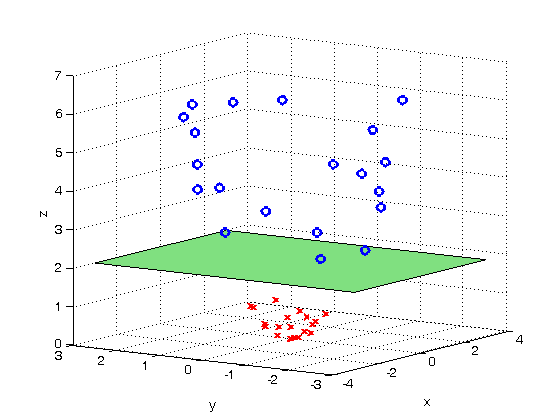
最后,我们将绿色空间的某部分投影到X-Y平面上,得到如图所示圆形分隔线,从而顺利分离红色和蓝色图标:
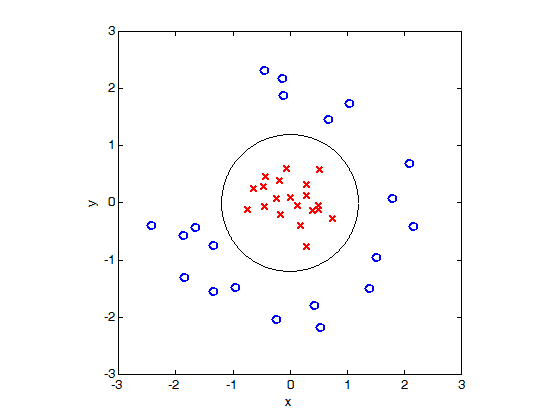
支撑向量机正是在这三个样例的情景中广泛应用。它的名字乍一听高端大气上档次,但其实质是一个找到那些“支撑着缓冲带数据点”的方法,就像有钱人的生活一样表面光鲜亮丽实则“朴实无华且单调”。
02
SVM 简概
为了解决更加复杂的问题,支持向量机学习方法有一些由简至繁的模型。具体来讲有三种情况:
线性可分支持向量机。当训练数据线性可分时,通过硬间隔最大化可以学习得到一个线性分类器,即硬间隔支持向量机。
线性支持向量机。当训练数据不能线性可分但是可以近似线性可分时,通过软间隔最大化也可以学习到一个线性分类器,即软间隔支持向量机。
非线性支持向量机。当训练数据线性不可分时,通过使用核技巧(Kernel Trick)和软间隔最大化,可以学习到一个非线性支持向量机。
03
SVM 三宝
最大间隔超平面
样例一中,二维空间上两类点可被一条直线完全分开叫做线性可分。对于线性可分严格的数学定义是:

如果将二维扩展到多维空间,能够将两个不同类别的点集完全正确地划分开的平面称为超平面。为了使这个超平面鲁棒性更好,我们会去找最佳超平面使其能按最大间隔把两类样本分开。这个最佳超平面必须具有更好的泛化能力,且对噪声不敏感。
那最佳超平面长什么样的呢?我们认为最佳超平面必须具有更好的泛化能力,对噪声更为不敏感,即有更好的鲁棒性。
从几何角度来说,两样本到超平面的间隔越大,其抗干扰能力越强,所以最佳超平面就是以最大间隔把样本分开的超平面,称之为最大间隔超平面。该平面具有以下两个特点:
两类样本分别分割在该超平面的两侧。
两侧距离超平面最近的样本点到超平面的距离被最大化。
原始与对偶
最优规划大体分两种,无约束规划 (Unconstraint) 和约束规划 (Constraint),下表给出两者的表现形式:

明显可以看出“约束”比“无约束”的规划问题困难,而为了解决这个问题,将“约束”转换成“无约束”,我们引入拉格朗日量(Lagrangian) :
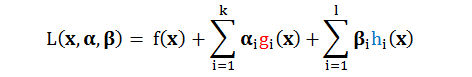
由上式可知,拉格朗日量L是 x, α, β 的函数,α 是和不等式类型的条件 (g) 相乘,而 β 是和等式类型的条件 (h) 相乘。现在假设,L 只在 α, β 上求最大值,而把x看作无影响的常数。用 θ 来表示这个关系,那么这个 θ 其实是 x 的一个函数,记作 θ(x)。
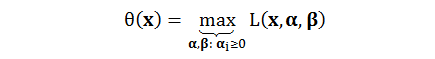
证明一:等价
1.若 x 违反了边界条件 (即:gi(x) > 0, hi(x) ≠ 0)
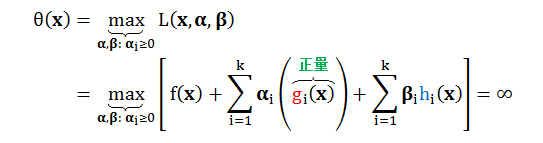
我们把f(x)看作常数,此时gi(x)为正数,若要θ(x)最大化,只要将 αi 调到无限大。当hi 大于0时,将 βi 调到无限大 ,反之调到无限小,那么 θ(x) 最大值为正无穷。
2:若 x 没有违反边界条件 (即:gi(x) ≤ 0, hi(x) = 0)
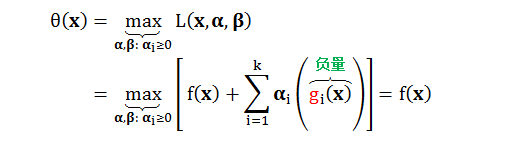
同样,我们把 f(x) 看作常数,此时gi(x)为负数,若要 θ(x) 最大化,则需要将 αi 调到0,此时 θ(x) 最大值为 f(x)。
总结来说:
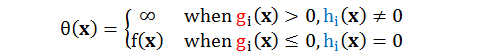
这样看,无约束最小化 θ(x) 就可以等价于有约束最小化 f(x) ,数学表达形式的对比如下:

简单来说,对于棘手的约束规划问题,可以用拉格朗日量转化成容易解的无约束问题,两者是等价的。
上表中无约束规划的形式叫做原始形式(Primal),与其对应的是对偶形式(Dual):
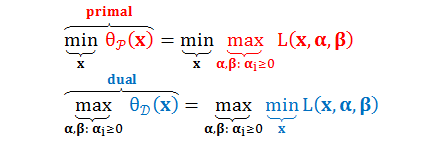
对于原始形式和对偶形式,下面不等式恒成立:
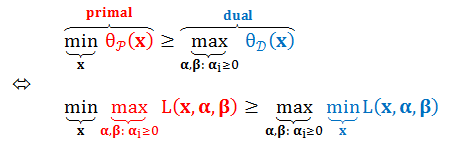
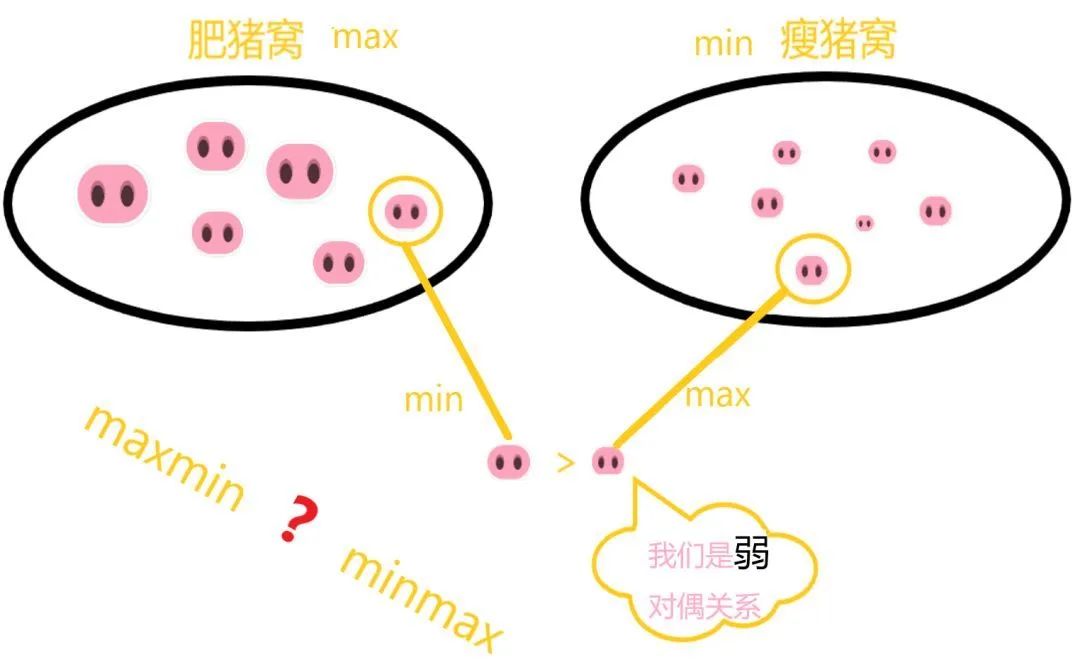
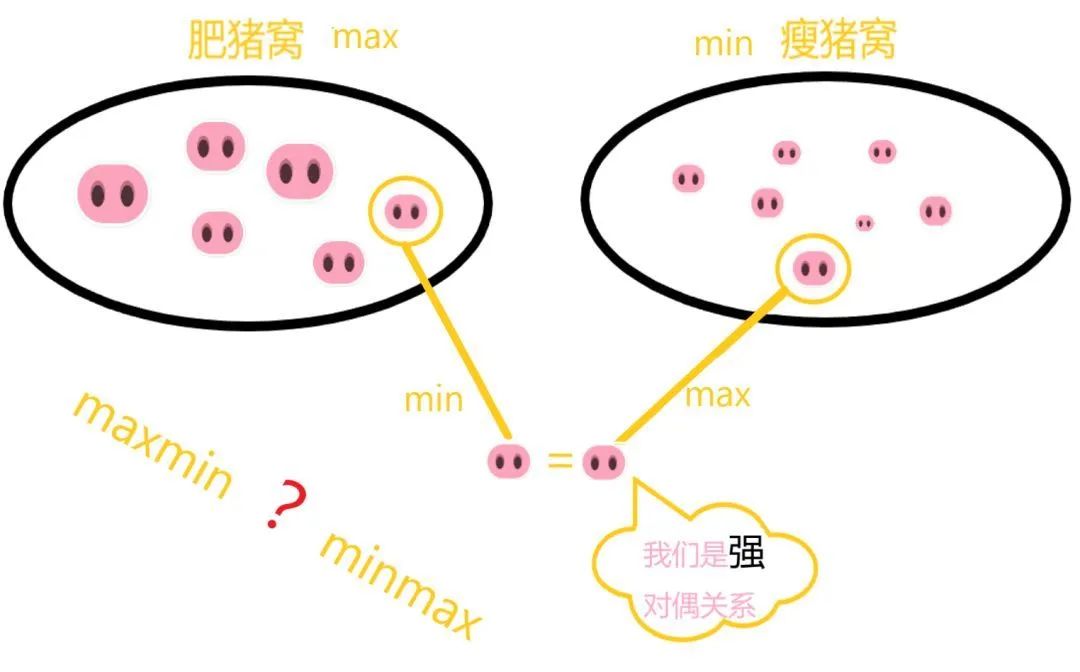
上述不等式被称为弱对偶性(Weak Duality),它表明“L最大值的集合中选出的最小值”永远大于等于“L最小值的集合中选出的最大值”,这很像中国的一句谚语——瘦死的骆驼比马大。弱对偶性的实际意义并不大,因为其对偶问题的最优解永远小于等于原始问题的最优解。
在实际问题中,我们想要原始问题和对偶问题的最优解一样,即原始问题和对偶问题等价,我们称之为强对偶(Strong Duality) 。强对偶等式如下图所示:
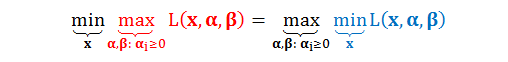
弱对偶可以附加以下三个约束条件(Constraint Qualification)转化为强对偶:
原始问题的目标函数是凸函数(Convex)
原始问题有解(Feasible Solution)
线性限制条件(Linear Constraints)
如果满足强对偶条件,可以将不好解的原始问题转化成好解的对偶问题,再用Karush-Kuhn-Tucker (KKT) 求解。假设x, α, β是最优解,它们满足KKT条件(强对偶的必要条件),如下:
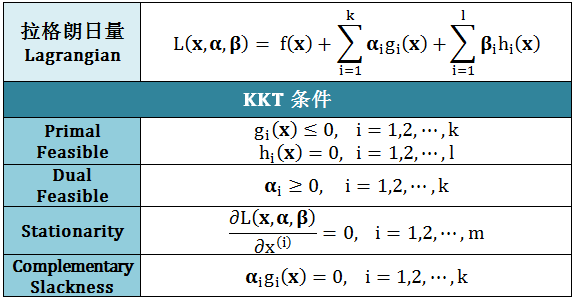
样例四:举例KKT条件
带不等式的约束条件的优化问题,一般会先转化为带等式约束,再通过拉格朗日乘子法为无约束,最后通过求导求解。
例如,给定约束条件 g(x) <= 0,求min f(x)。我们首先定义一个k值,使得 h(x,k) = g(x) + k^2。接着定义如下拉格朗日函数(λ为拉格朗日乘子):L(x,λ,k) = f(x) + λh(x) = f(x) + λg(x) + λk^2,即把约束不等式转为无约束等式,最后分别对各个参数求导。此处优化问题为例,讲讲带不等式的约束条件时怎么求解的:
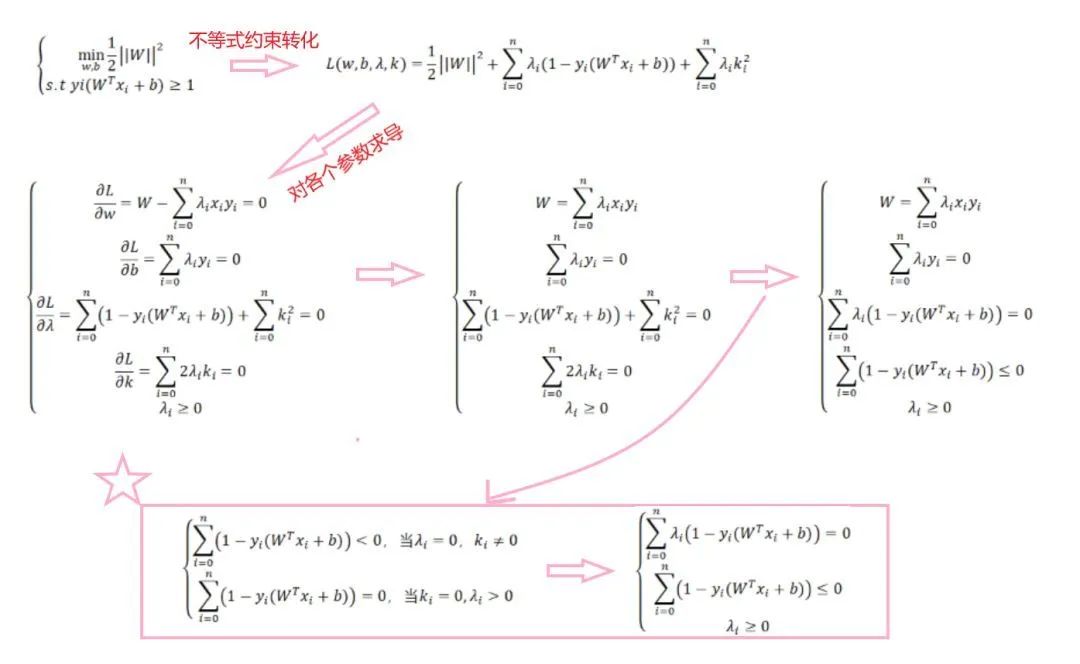
从上图星号公式可知:只有当 λi > 0 时,约束条件才起约束作用,此时的点(xi, yi)称为支持向量,这也是为什么这个算法叫“支持向量机”。由于真正对最佳超平面起作用的点只有支持向量,算法的研究运算消耗大大降低。
那么强对偶能解决什么问题呢?强对偶可以根据计算的难度、复杂度使问题在minmax与 maxmin之间转换。
核函数
这个部分将在《探索支持向量机(三)》中具体讲解。此处仅做简单说明:支持向量机通过某非线性变换 φ(x),将输入空间映射到高维特征空间。如果支持向量机的求解只用到内积运算,且在低维输入空间存在某个函数 K(x, x′) 的输出恰好等于在高维空间中 φ(x) 的内积,即 K(x, x′) = <φ(x), φ(x′)> 。那么支持向量机可以不用计算复杂的非线性变换,而由函数 K(x, x′) 直接得到非线性变换的内积,从而大大简化计算。这样的函数 K(x, x′) 被称为核函数。
至此,本文仅仅是带领大家初步认识下支持向量机,后续推文笔者将带大家深入了解下不同类别的支持向量机内在原理:
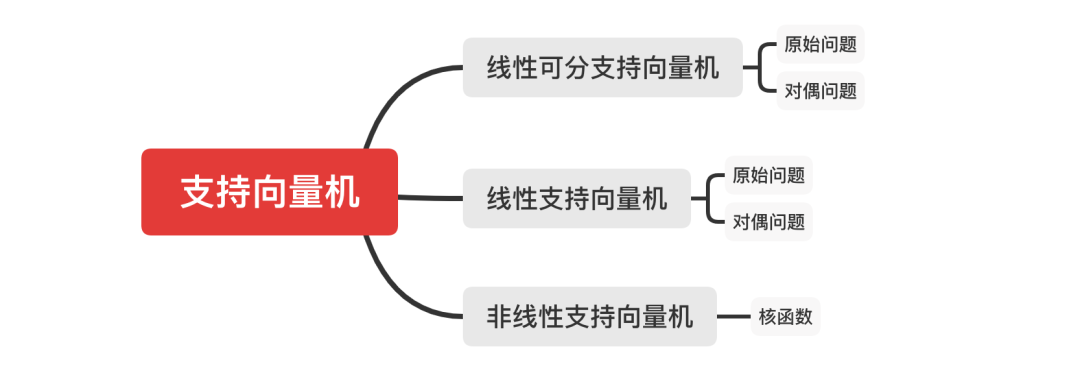
感谢大家的支持,我们下期再见!
应用之道
END
存乎一心
本文作者:Bingunner
一位头发浓郁的信息安全工程师
爱摄影/爱数码/爱跑步的经济学人死忠粉









