点击蓝字关注我们
应用之道
存乎一心


本文承接《【CNN】认识卷积神经网络(一)》和《【CNN】认识卷积神经网络(二)》,以下分别简称“文一”、“文二”。本文主要介绍卷积神经网络的采样层(Pooling Layer)、全连接层(Fully-connected Layer)其它相关概念。本文中如有错误,欢迎大佬们指正!
01
采样层
原始图像经过卷积层之后输出特征图(Feature Map),特征图将继续经过采样层(又称池化层),采样层处理操作被称为池化(又称下采样)。池化可以进一步降低每个特征映射的维度,并保留最重要的信息。池化有几种不同的方式:最大值(Max-pooling ),平均值(Average-pooling),求和(Sum-pooling)等。
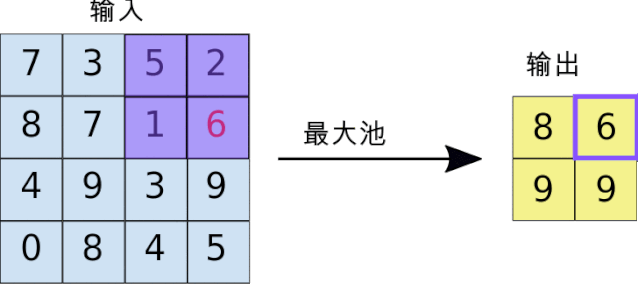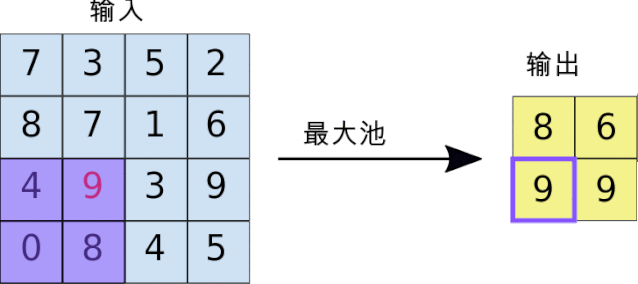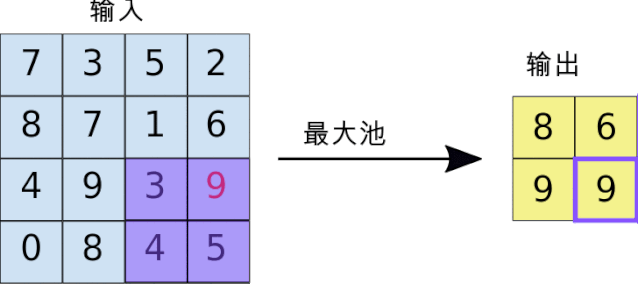
上图演示了最大池化如何进行:我们定义一个2 × 2窗口(紫色),并取特征图在该窗口内最大的元素,即选出这个区域内选出最有代表性的值,然后丢掉那些没多大用的信息,最后输出2X2窗口(黄色)。正因如此,池化后的数据量也将大大减少。当然我们也可以取该窗口内所有元素的平均值(平均池化)或所有元素的总和(求和池化)。采样层常见参数设置为2X2窗口,步长为2。
特别提醒
1.特征提取的误差主要来自两个方面:
邻域大小受限。
卷积层权值参数误差。
2.不同池化方式的侧重点也有所不同:
平均池化能减小第一种误差,保留更多的图像背景信息。
最大池化能减小第二种误差,更多的保留纹理信息。
下图我们演示如何对一个6X6的特征图进行池化,你会发现操作逻辑与对原始图像卷积的逻辑相似,只不过采样层的池化操作选取的是区域最大值,而卷积层操作进行的是卷积运算:
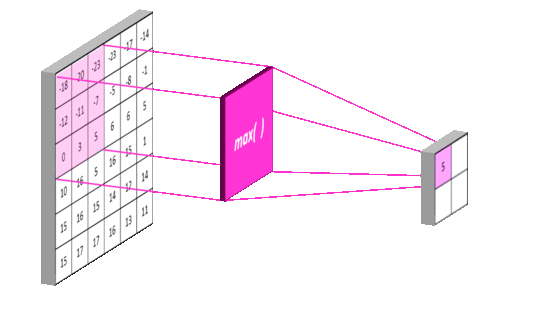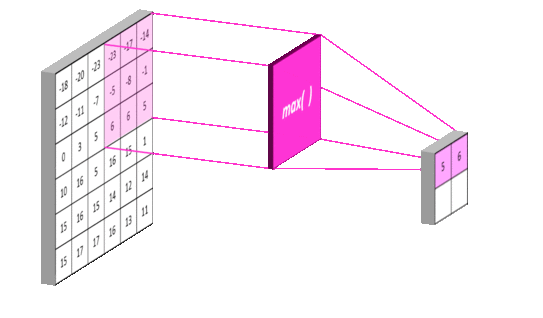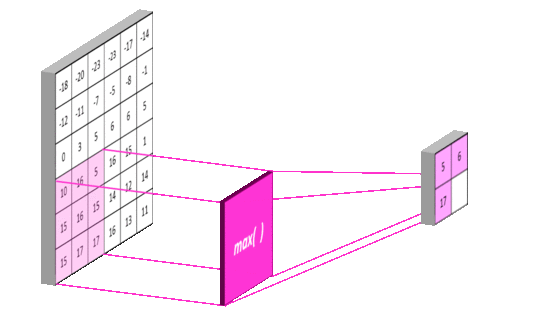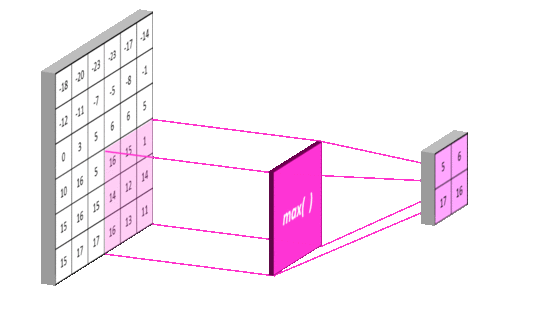
池化的作用是逐步减少输入的空间大小。具体来说有以下三点:
特征降维:使输入(特征维度)更小,更易于管理,减少网络中的参数和运算次数,因此可以控制过拟合 。
特征不变:使网络对输入图像微小的变换、失真和平移更加稳健。
一定程度上防止过拟合。
笔者将通过两个样例进一步解释池化的作用,以下这些极为有(bian)趣(tai)的样例依然参考自知乎蒋竺波同学:
样例一:如何进行池化
下面四个美女如果非要选,你会娶谁?

正常人肯定会选最漂亮的那个(即最符合的特征),至于其它的你会考虑吗?(反正笔者不会……)当然,如果有天赋异禀的读者会表示:“小孩子才做选择,成年人我都要!”(即不做最大池化),笔者只能先干为敬……

假设有人(承认吧,就是你)坚持4个全部娶回家。首先,她们会各种勾心斗角让你崩溃(过拟合)。然后你会有巨大的经济压力,身体也吃不消(参数过多运算量大)。

最后可能你还会难以平衡婆(上一卷积层)媳或者母子(下一卷积层)关系(即无法满足模型结构需求)。所以现在你还想娶4个吗?

样例二:池化的意义
采样层还可以在一定程度提高空间不变性,比如说平移不变性,尺度不变性,形变不变性等等。上一层卷积本身就是对图像局部卷积,因此卷积神经网络中重要的是单独区域的特征以及特征之间的相对位置。而图像细微的变换经过卷积,最大池化之后,输出结果和原来差别可能不大。比如,在池化矩阵范围内,小小平移依然产生相同的池化特征,即平移不变性(Translation Invariant)。举个例子,我们在纸上不同位置写上数字“2”,即使位置不同我们依然希望机器识别出来这是数字“2”。
特别提醒
1.多个卷积层和采样层的意义
实际上,卷积和采样层操作可以在一个卷积神经网络中重复执行多次。效果最好的一些卷积神经网络都包含几十个卷积和采样层 。如下图所示,随着层数越多,提取到的小狗特征越丰富:

2.采样层并不是必须的
每个卷积层之后的采样层不是必需的。采样层说到底还是一个特征选择、信息过滤的过程。采样层通过降低输入的尺寸变相减少整个网络的参数,即为了计算性能而损失部分信息、降低了分辨率。但随着运算速度的不断提高,现在有些网络都开始少用或者不用采样层。
02
激活函数
实际上,下采样层出来的结果并不是直接卷积层,而是进入了一个激活函数(Activation Function)。如下图所示,各种激活函数层数不穷,各有优缺点。比如Sigmoid 只会输出正数并且靠近0处的输出变化率最大。而Tanh和Sigmoid就有所不同,Tanh输出可以是负数。再比如,ReLu是输入只能大于0,如果输入含有负数ReLu就不太适合,而如果输入是图片格式,ReLu比较常用的。因此,需要根据实际情况灵活考虑输入输出以及数据变化,从而谨慎选择激活函数。
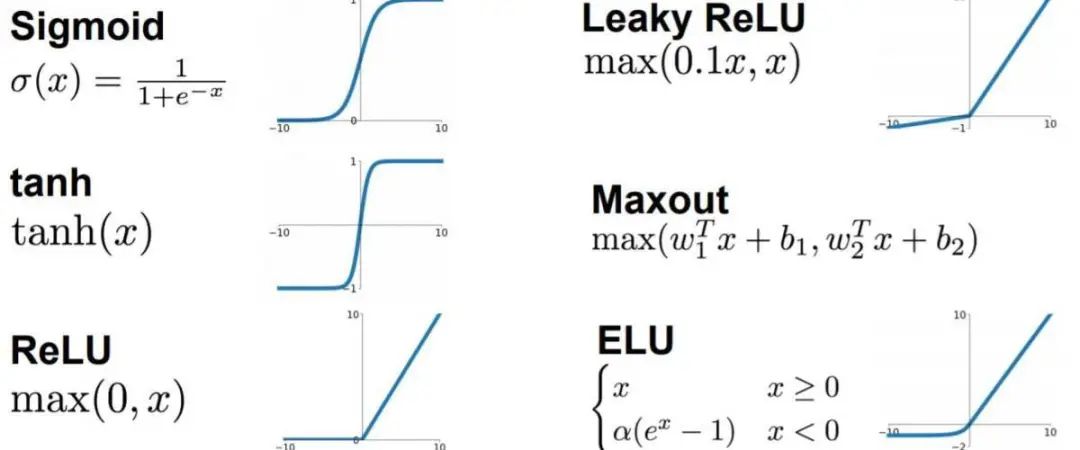
样例三:激活函数的作用
我们究竟需要解决什么问题呢?主要有以下四个:
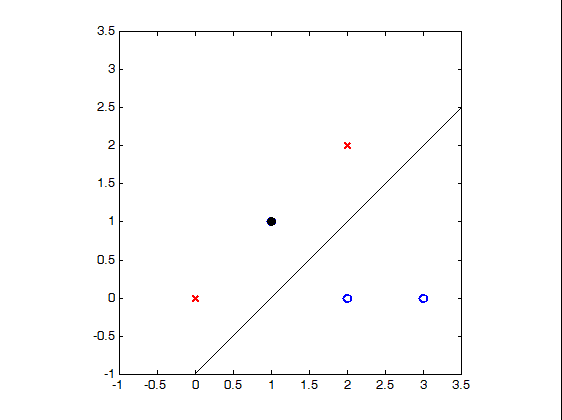
线型神经网络无法解决非线性问题。下方左图可以用一条直线将两类图形分开,而右图无法找到一条直线将两类图形分开,我们称右图中的问题为“非线性问题”。由于线性函数具有可加性和齐次性,任意线性函数连接都可以等价为一个单一线性函数。因此,叠加简单神经网络解决不了非线性分类问题。

需要对神经网络的输出分类。假设神经网络有Y = W*X + B,根据input X的值我们可以得到Y值。现在我们需要一个函数可以对得到的Y值进行分类。比如,Y大于0 时分为类别1,Y小于0 分为类别0。
对于神经网络,我们需要算出输出误差来更新权值。假设我们的输入X的绝对值特别大或者无限大,那么Y值就会特别大。这将直接导致误差太大,更新出来的权值没有意义或者无法更新权值。
如果我们的神经网络函数是线性的,那么它的导数就是个常数。这意味着梯度和X无关了,即与输入无关。我们在做反向传播的时梯度的改变也变成常数,即与输入的改变无关。
激活函数确实是很好宽广的点,它能提高模型鲁棒性及非线性表达能力、缓解梯度消失问题并能将特征图映射到新的特征空间从何更有利于训练。
简单来讲,先池化后激活和先激活后池化得到的效果是一样的,先池化进行了下采样,那么在激活函数的时候就减少了消耗
特别提醒
卷积层、采样层、激活函数先后顺序
一般来说,先池化后经过激活函数和先经过激活函数后池化得到的效果一样。但先池化(即下采样),再经过激活函数的时候能减少消耗。
03
全连接层
最后一层卷积层和采样层的输出经过激活函数后将到达全连接层。完全连接层是一个传统的多层感知器,它在输出层使用 softmax 激活函数(也可以使用其它分类器,比如 SVM)。全连接层之前的作用是提取特征,而全连接层的作用是分类。
“完全连接”这个术语意味着前一层中的每个神经元都连接到下一层的每个神经元。卷积层和采样层的输出代表了输入图像的高级特征。完全连接层的目的是利用这些基于训练数据集得到的特征,将输入图像分为不同的类。
除分类之外,添加完全连接层也是一个(通常来说)比较简单的学习这些特征非线性组合的方式。卷积层和采样层得到的大部分特征对分类的效果可能也不错,但这些特征的组合可能会更好。
需要注意的是,卷积、池化、激活函数之后的输出数据无法直接连接全连接层,需要先把全连接层之前数据展平(Flatten),即把多维的输入一维化。为了更好的进行讲解,笔者以鸟类图片分类为例。如下图所示,假设鸟类图片经过卷积、池化、激活函数之后输出5个3X3的特征图。
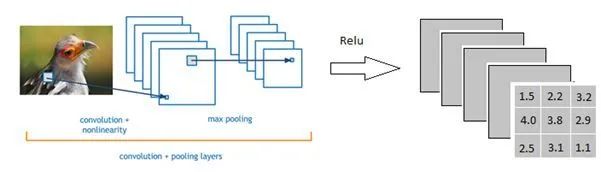
然后我们将这5个3X3特征图输入到全连接层。如下图所示,仔细观察可以发现全连接层中的每一层是由许多神经元组成,即1x 4096的平铺结构。
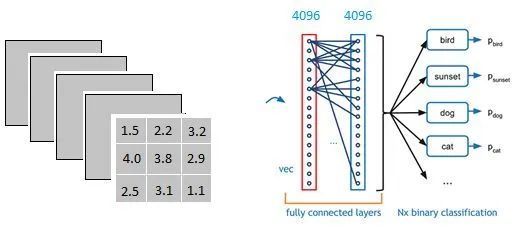
但它是如何把卷积、池化、激活函数后的3x3x5输出转换成1x4096的形式呢?
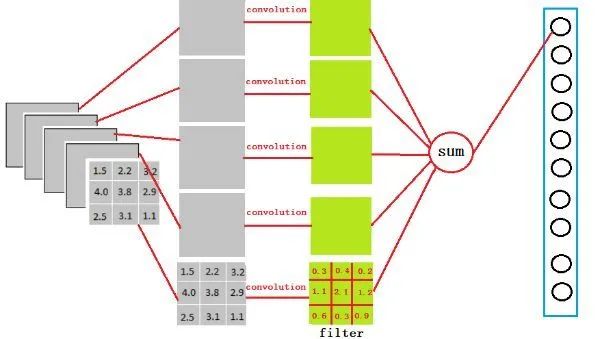
从上图可以看出,使用一个3x3x5的f过滤器去卷积激活函数的输出,得到的结果就是全连接层一个神经元的输入。由于此处全连接层有4096个神经元,实际就是用一个3x3x5x4096的卷积层去卷积激活函数的输出既可以达到展平的效果。
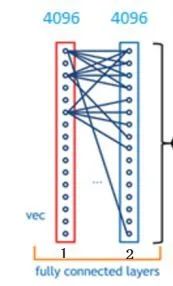
另外,图中可以发现全连接层并不只有一层,因为一层全连接层有时候没法解决非线性问题,而如果有两层或以上的全连接层就可以很好地解决非线性问题。就像泰勒公式一样,全连接层中一层的一个神经元就可以看成一个多项式,多项式越多越贴近拟合的光滑函数(太多反而会出现过拟合现象且训练过程的计算量巨大)。
样例四:展平的深层含义
展平操作实际上是把特征表达整合到一起,然后输出为一个值,这样可以大大减少特征位置对分类带来的影响。举个例子,假设我们现在对猫的图片分类:
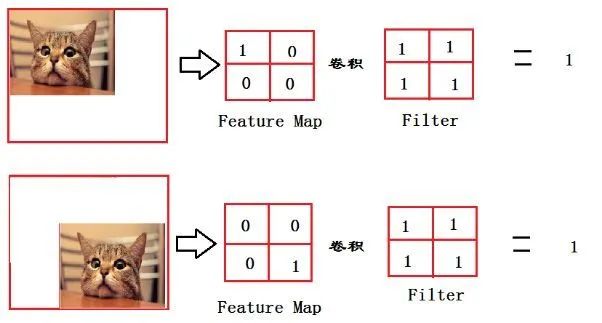
从上图我们可以看出,猫在不同的位置,输出特征图(Feature Map)的特征值相同,但位置不同(一个1在左上,一个在右下)。对于计算机来说,如果特征值相同但特征值位置不同,其分类结果也可能不同。
这时展平操作相当于让过滤器直接锁定猫猫,忽略猫的位置的差异。实际就是把特征图整合成一个值,值大的代表有猫,值小的代表可能没有猫,模型的鲁棒性得以大大增强。但展平后空间结构特性却被忽略了,所以全连接层不适合用于在方位上寻找模式任务的情形。
特别提醒
全连接层并不是必须的
目前由于全连接层参数冗余(仅全连接层参数就可占整个网络参数80%左右),近期一些性能优异的网络模型如ResNet和GoogLeNet等均用全局平均池化(Global Average Pooling,GAP)取代全连接神经网络来融合学到的深度特征,最后仍用softmax等损失函数作为网络目标函数来指导学习过程。
至此,《【CNN】认识卷积神经网络》系列全部更新完毕,笔者仅对卷积神经网络做了一个“肤浅”的介绍,后续笔者也将继续对卷积神经网络进一步学习,感谢大家的关注!
应用之道
END
存乎一心
本文作者:Bingunner
一位头发浓郁的信息安全工程师
爱摄影/爱数码/爱跑步的经济学人死忠粉







