Learning Important Features Through Propagating Activation Differences
DeepLIFT:为给定输出的输入分配重要性得分的新颖算法。DeepLIFT将每个神经元的激活与其“参考激活”进行比较,并根据差异分配贡献分数;通过分别考虑正面和负面贡献,DeepLIFT还可以揭示其他方法遗漏的依赖关系;另外,DeepLIFT得分可以在一次后向传播中有效地获得。
本文研究问题:机器学习的可解释性。
机器学习的可解释性,包括两个方面:一是局部可解释性,二是全局可解释性。
以猫分类器为例,局部可解释性是指为什么觉得这张图片是一只猫?而全局可解释性是指“猫”这个类别长什么样子?
与全局可解释性不同,模型的局部可解释性以输入样本为导向,通常可以通过分析输入样本的每一维特征对模型最终决策结果的贡献来实现。在实际应用中,提供对机器学习模型的全局解释通常比提供局部解释更困难,因而针对模型局部可解释性的研究更加广泛。
本文研究属于机器学习模型的局部可解释性范畴,研究的目标是使深度学习更具解释性,以便我们在使用强大的模型的同时也能深入了解它们为何起作用。
在这项工作中,主要关注于特定示例的解释。也就是说,对于给定的示例和输出,目标则是为输入的各个部分分配重要性得分。例如,如果输入是DNA序列,而输出是某种蛋白质是否与该序列结合,目标就是突出显示序列中与预测该蛋白质是否结合最相关的位置。
输入示例:

突出显示:

相关方法
1.基于扰动的正向传播方法
原理:对单个输入或神经元产生干扰,并观察对神经网络中后续神经元的影响。
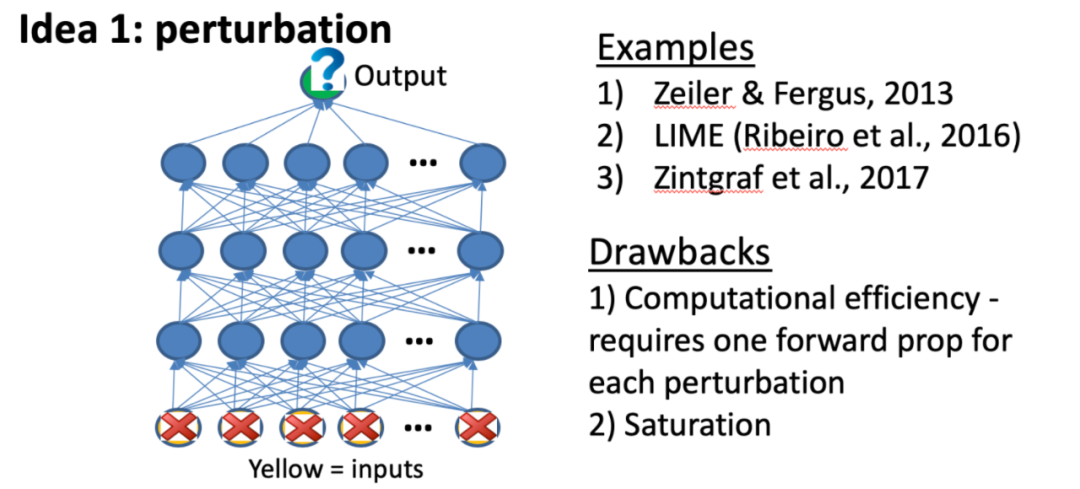
最早的此类方法由Zeiler&Fergus在2013年提出,他们用滑动窗口遮挡图像的不同部分,并观察输出的变化。LIME也属于这一类,它使用从输入扰动中收集的数据建立线性模型来近似网络的局部行为。
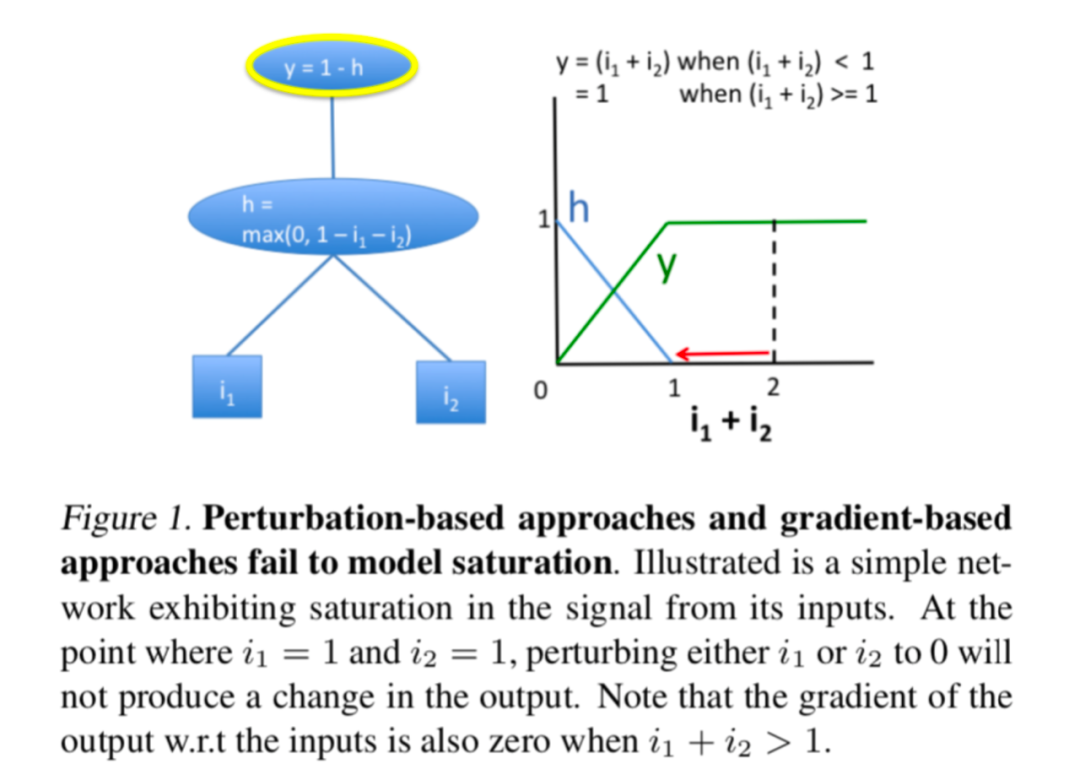
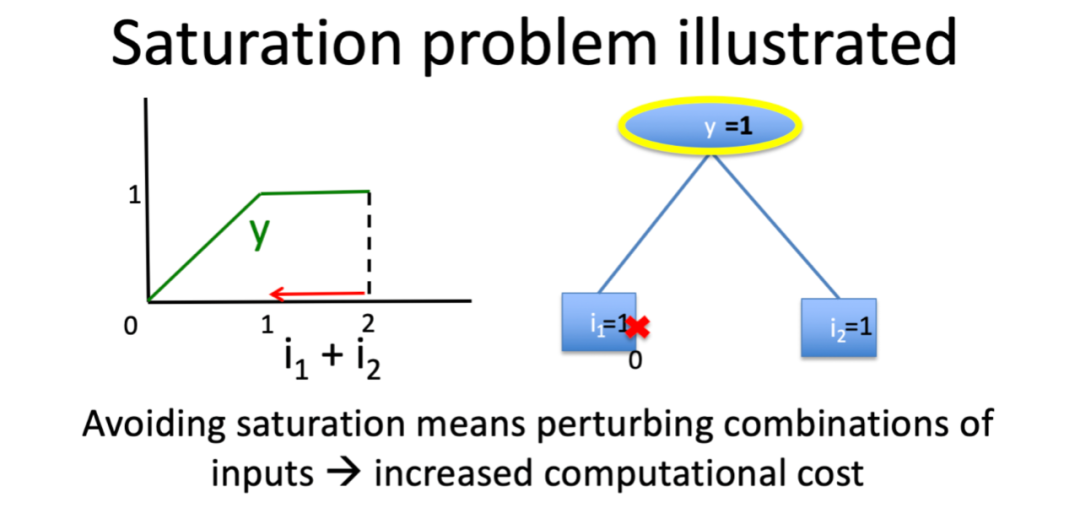
缺陷:由于每次扰动都需要通过网络进行单独的正向传播,因此这些方法在计算上效率低下。另一个问题就是饱和问题,可能低估满足输出贡献的特征的重要性。
饱和问题:
2.基于反向传播的方法
原理:将重要信号从输出神经元通过各层反向传播到输入神经元,使之高效。
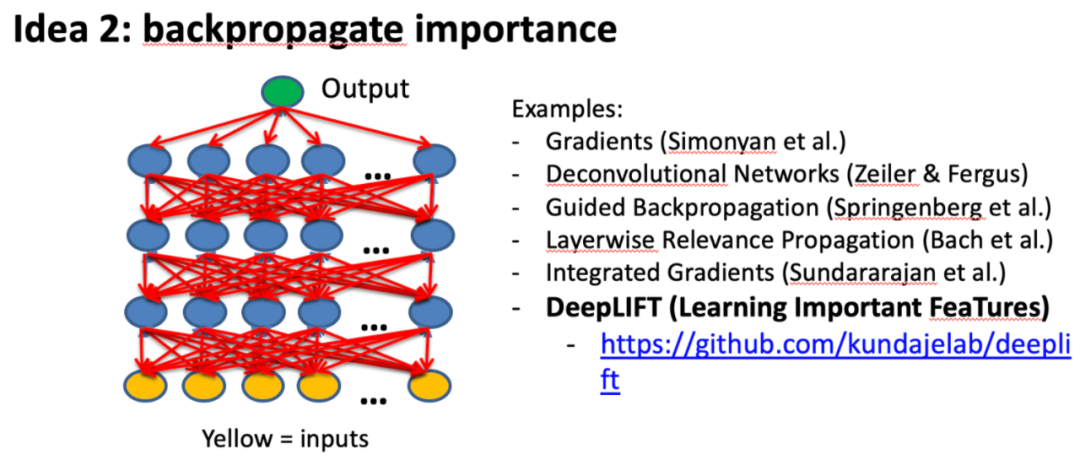
Gradients
Simonyan 等人最先提出了利用反向传播推断特征重要性的解释方法(Grad),具体地,Grad方法通过利用反向传播算法计算模型的输出相对于输入图片的梯度来求解该输入图片所对应的分类显著图(Saliency Map)。如下图,亮度越高的区域代表这个Pixel对于预测结果的影响越大。

Deconvolutional Networks
Zeiler 等人提出了反卷积网络(DeconvNet),通过将 DNN 的高层激活反向传播到模型的输入以识别输入图片中负责激活的重要部分。
Guided Backpropagation
Springenberg 等人将 Grad 方法与反卷积网络相结合提出了导向反向传播方法(GuidedBP),通过在反向传播过程中丢弃负值来修改 ReLU 函数的梯度。
总结:
从本质上说,反卷积和导向反向传播的基础都是反向传播,其实说白了就是对输入进行求导,以上三者唯一的区别在于反向传播过程中经过ReLU层时对梯度的不同处理策略。
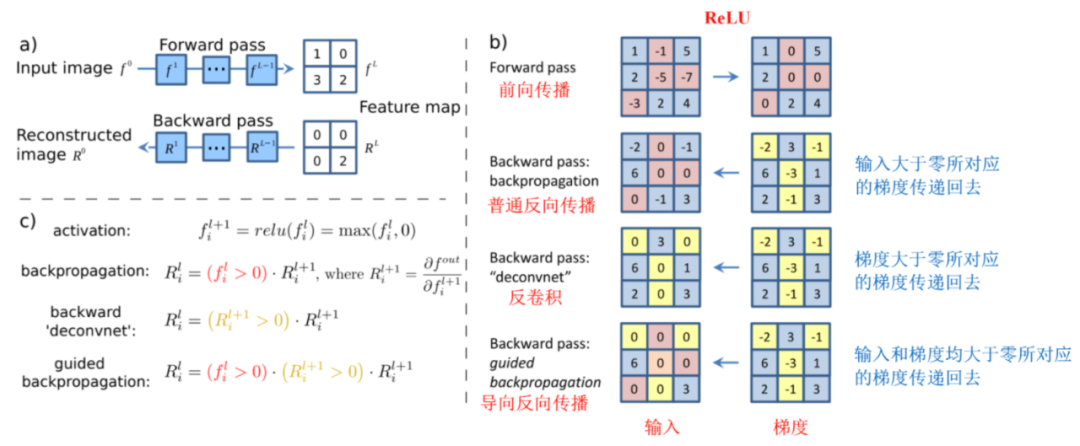
缺陷:由于负梯度归零,所以反卷积和导向反向传播并不能突出显示对输出有负面贡献的输入;另外,以上三种方法都不能解决饱和及阈值伪影问题(梯度的不连续性会导致不需要的伪影)。
LRP
Bach 等人提出了一种分层相关性传播方法(LRP),用于计算单个像素对图像分类器预测结果的贡献,LRP 的核心是利用反向传播将高层的相关性分值递归地传播到低层直至传播到输入层。Shrikumar和Kindermans的研究表明,在不修改数值稳定性的情况下,原始LRP规则在比例因子内等价于显著性图和输入之间的元素积,也就是梯度×输入。
缺陷:梯度×输入通常会比单独使用梯度效果更好,因为它会利用输入的符号和强度,但仍无法解决饱和及阈值伪影问题。
Integrated Gradients
与只计算输出针对当前输入的梯度不同, Sundararajan 等人提出了一种集成梯度方法(Integrated),该方法通过计算输入从某些起始值按比例放大到当前值的梯度的积分代替单一梯度,有效地解决了 DNN 中神经元饱和问题导致无法利用梯度信息反映特征重要性的问题。
缺陷:从数值上获得高质量的积分会增加计算开销;此外,这种方法仍会产生误导性的结果。
3.Grad-CAM and Guided CAM
Grad-CAM(Selvaraju等人,2016)通过基于每个类别的梯度将最终卷积层中的特征图与特定类别相关联来计算粗粒度特征重要性图,然后使用特征图的加权激活来指示哪些输入最重要。为了获得更细粒度的特征重要性,作者建议在从Grad-CAM获得的得分与从导向反向传播获得的得分(称为Guided CAM)之间执行元素乘积。
缺陷:该两种策略继承了反向传播过程中负梯度归零导致的局限性。
本文方法
DeepLIFT: 为给定输出的输入分配重要性得分的新颖算法。
独特性:
1.它根据与“参考”状态的差异来描述重要性的问题,“参考”状态依目前问题而定
解决梯度的基本限制
与大多数基于梯度的方法相比,即使在梯度为零的情况下,使用参考差异也能允许神经元传播重要信号。
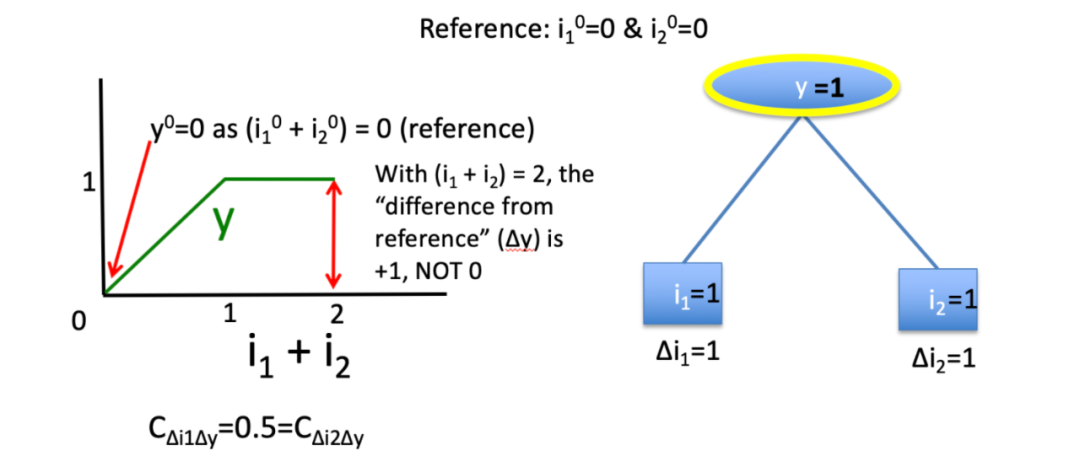
解决了由梯度不连续而导致的伪影
梯度的不连续性会导致重要性分数在输入中的无穷小变化上突然跳跃。相比之下,参考差异是连续的,从而使DeepLIFT避免了由偏置项引起的不连续性。
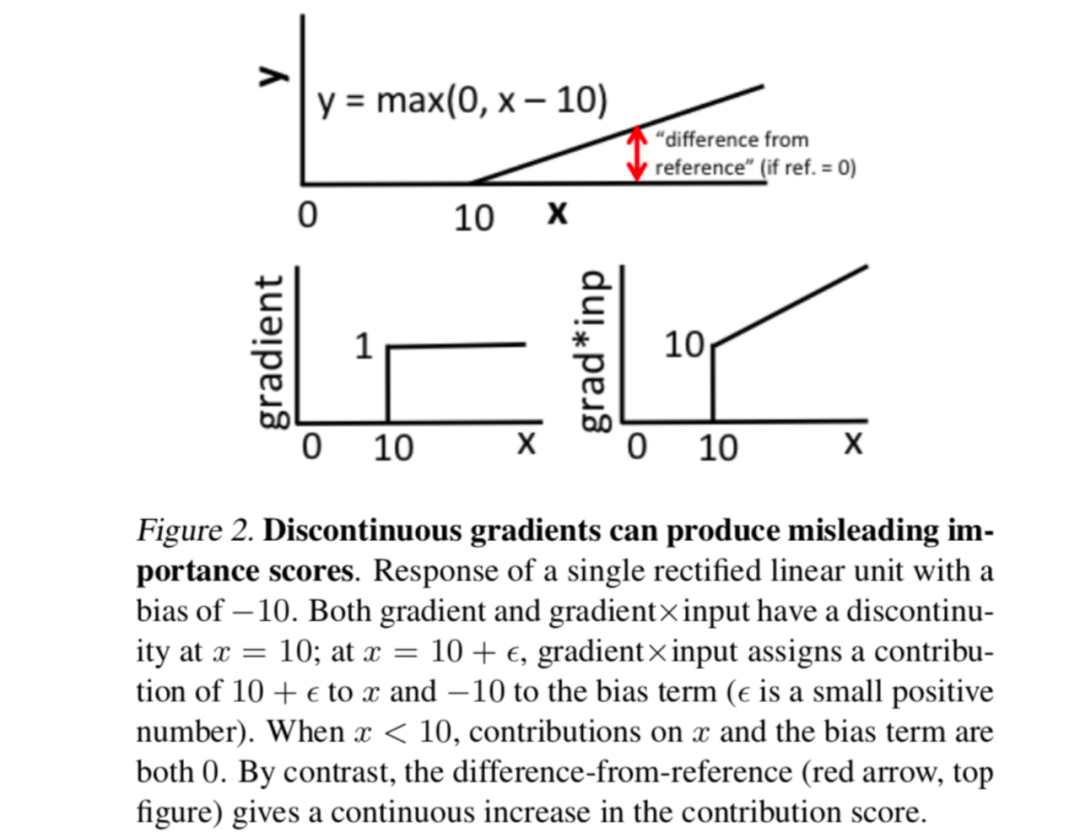
2.通过选择性的分别考虑非线性中正负贡献的影响,DeepLIFT可以揭示其他方法遗漏的依赖性。
由于DeepLIFT得分是使用类似反向传播的算法来计算的,因此在做出预测后,可以在一次反向传播中有效地获得。
1.DeepLIFT理论
DeepLIFT用一些“参考”输入的输入差异来解释某些“参考”输出的输出差异。(“参考”输入代表一些默认或“中性”输入,这些输入是根据适合当前问题的情况选择的)
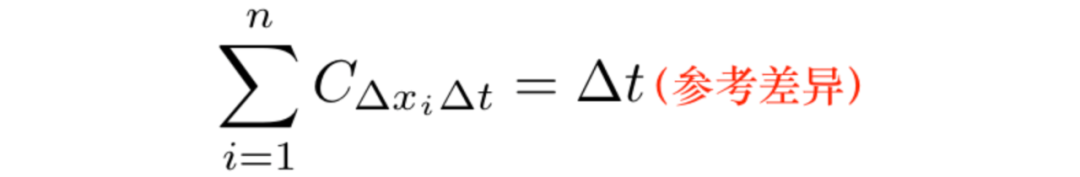
2.乘数与链式规则
乘数的定义:
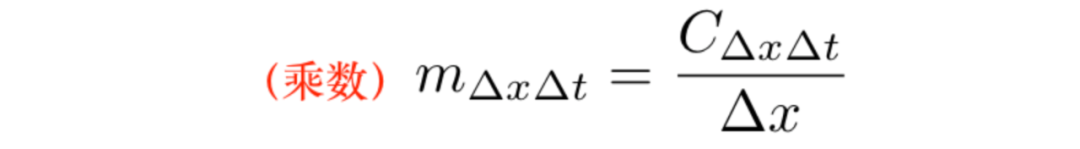
乘数在本质上与偏导数相似,但是乘数是有限的,而不是无穷的。
乘数的链式法则:
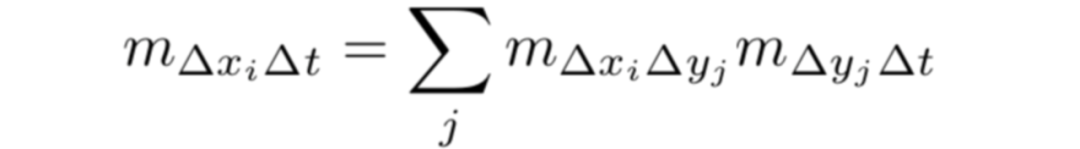
给定每个神经元与其直接后继的乘数,我们可以通过反向传播有效地计算任何神经元与给定目标神经元的乘数。
3.定义参考
参考:神经元的参考为其在参考输入上的激活
输出的参考激活计算: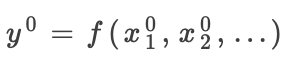
参考输入的选择对于从DeepLIFT获得深入的结果至关重要。实际上,选择一个好的参考将依赖于特定领域的知识,在某些情况下,最好针对多个不同的参考来计算DeepLIFT分数。
注意:梯度x输入隐式地使用全零的引用;积分梯度要求用户指定积分的起点,类似于为DeepLIFT指定参考;Guided Backprop和纯梯度不使用参考,但我们认为这是一个局限,因为这些方法仅描述特定输入值下输出的局部行为,而没有考虑输出在输入范围内的行为 。
4.区分正面和负面贡献
对于每个神经元
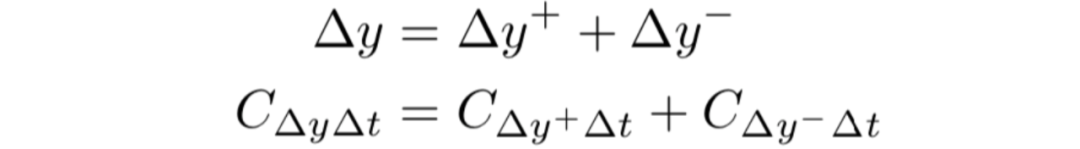
5.分配贡献得分的规则
我们提出将每个神经元的贡献分数分配给其直接输入的规则。结合乘数的链式规则,这些规则可用于查找任何输入(不仅是立即输入)通过反向传播对目标输出的贡献。
线性规则
适用于卷积层(不包括非线性)。假设y是其输入的线性函数: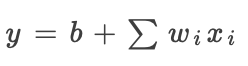 ,我们将
,我们将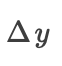 的正负部分定义为:
的正负部分定义为:
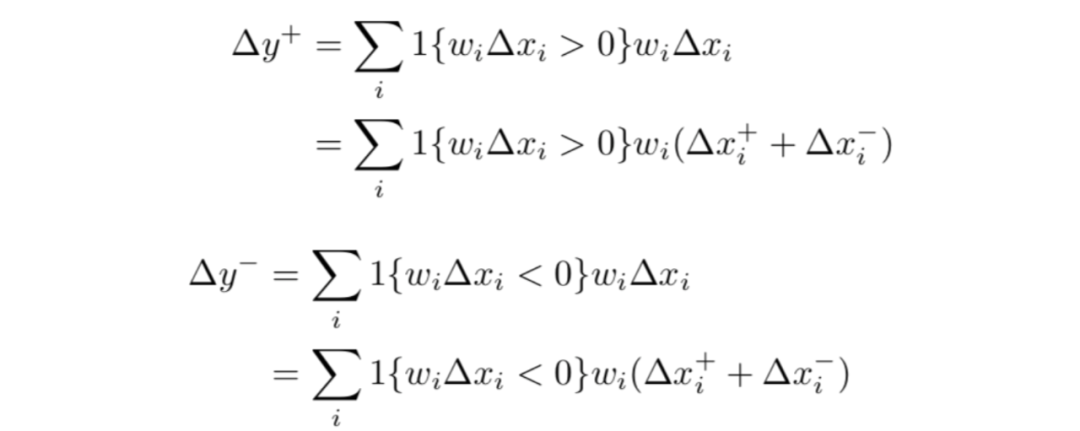
贡献选项则有:
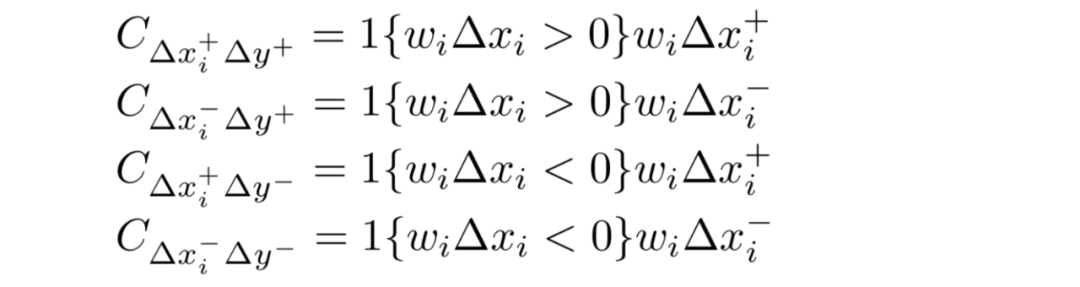
由之前乘数定义:
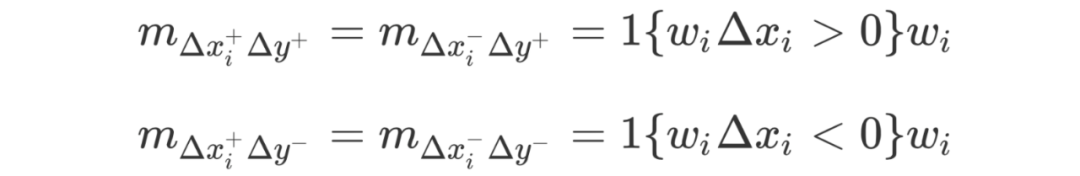
当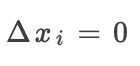 时:
时:

Rescale规则
适用于采用单个输入的非线性转换,如ReLU、tanh和sigmoid运算。假设是其输入的非线性转换: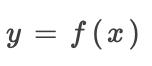 ,通过求和得出:
,通过求和得出: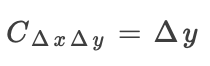 ,因此:
,因此: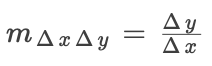

当
注意:Rescale规则解决了饱和和阈值问题。即使在梯度为零的情况下,使用参考差异也可以使信息流动。
RevealCancel规则
尽管Rescale规则仅使用了梯度就得到了改进,但在某些情况下它可能会产生误导性的结果。

如图是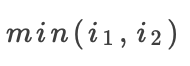 运算,假设参考值
运算,假设参考值 均为0,运用the Rescale rule,所有重要性都将分配给较小者,这就会掩盖两个输入都与最小操作相关的事实。
均为0,运用the Rescale rule,所有重要性都将分配给较小者,这就会掩盖两个输入都与最小操作相关的事实。
解决此问题的一种方法是分别处理正面和负面贡献。我们再次考虑非线性神经元 ,重新定义如下:
,重新定义如下:
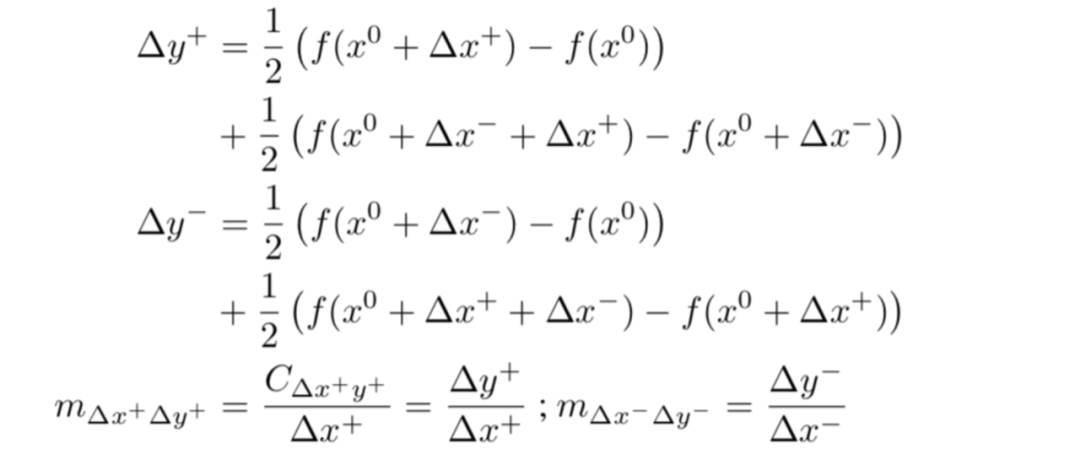
换句话说,我们在未添加任何条件之后和在添加了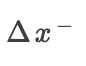 之后将
之后将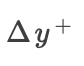 设置为
设置为 的平均影响,在未添加任何条件之后和在添加了
的平均影响,在未添加任何条件之后和在添加了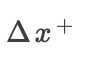 之后将
之后将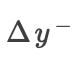 设置为
设置为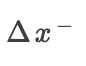 的平均影响。
的平均影响。
6.目标层的选择
对于softmax或sigmoid输出,我们可能更喜欢计算最终非线性之前的线性层贡献,而不是最终非线性本身,这样可以避免summation-to-delta 特性引起的衰减。
Softmax图层的调整
可能出现的问题是,最终的softmax输出涉及所有类的归一化,但softmax之前的线性层不涉及。解决:通过减去对所有类的平均贡献来规范化对线性层的贡献。
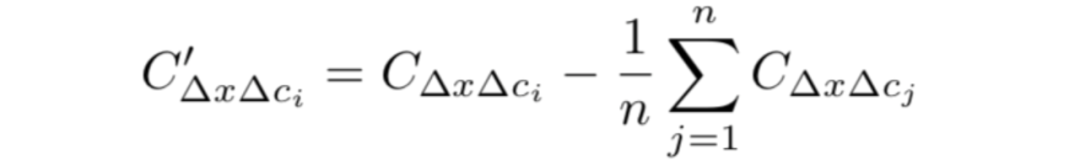
理由:从所有输入减去softmax的固定值后,softmax的输出保持不变。
实验与结果
Digit Classification (MNIST)
任务:给定原始图像属于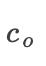 类,我们识别哪些像素需要擦除,以将图像转换为目标类
类,我们识别哪些像素需要擦除,以将图像转换为目标类 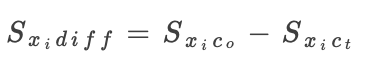 ,之后将大于0的
,之后将大于0的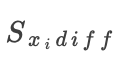 按降序排列,擦除多达157个对应像素(占图像的20%)。然后,我们评估原始图像和擦除像素的图像在
按降序排列,擦除多达157个对应像素(占图像的20%)。然后,我们评估原始图像和擦除像素的图像在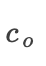 和
和
带有RevealCancel规则的DeepLIFT可以更好地识别像素,以将一个数字转换为另一个数字。

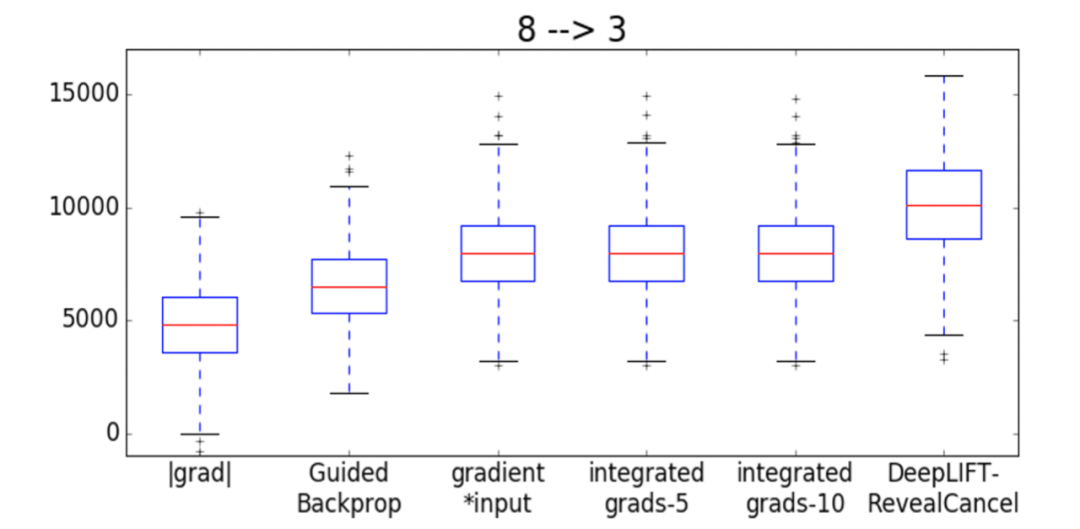
Classifying Regulatory DNA (Genomics)
带有RevealCancel规则的DeepLIFT在TAL-GATA模拟上给出了定性的理想行为
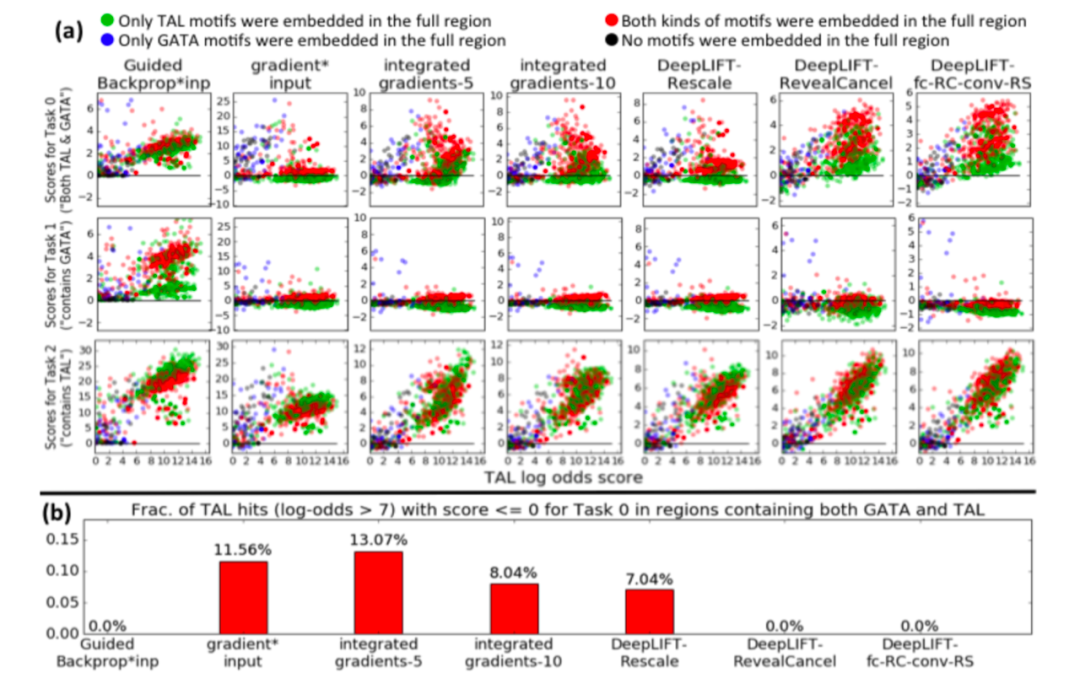
RevealCancel突出显示任务0的TAL1和GATA1 motifs 。
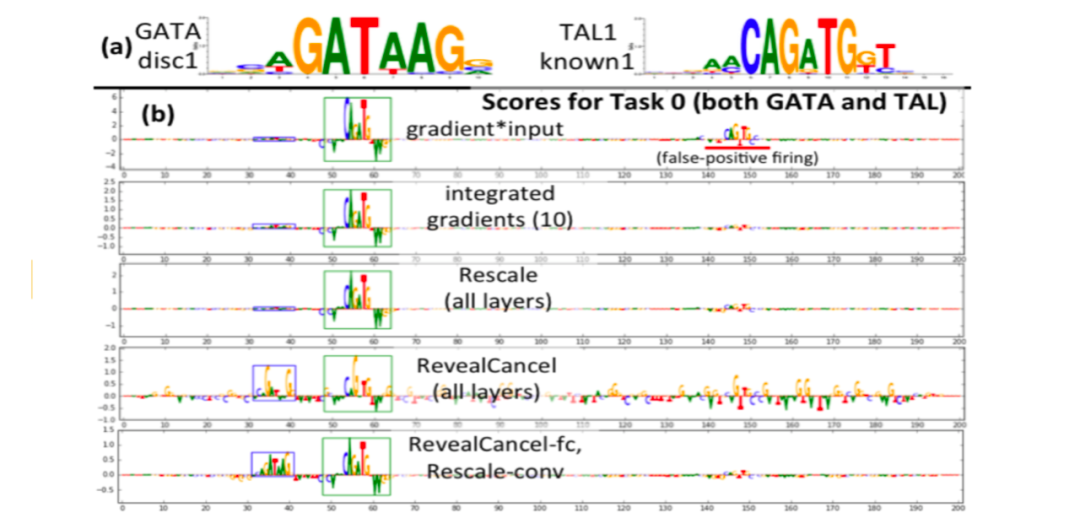
本文结论
贡献:DeepLIFT:一种计算重要性得分的新颖方法,其依据是根据“参考”输入的输入差异来解释某些“参考”输出的输出差异。
使用参考差异可以使信息即使在梯度为零的情况下也能传播;DeepLIFT避免了偏差项可能具有的误导性的重要性;通过分别对正负贡献进行处理,DeepLIFT可以识别其他方法遗漏的依赖关系。
尚待解决的问题:
如何将DeepLIFT应用于RNN,如何从数据中凭经验计算出良好的参考,以及如何通过“max”操作(如在Maxout或Maxpooling神经元中)以最佳方式传播重要性,而不仅仅是使用梯度。
点击“阅读原文”,了解论文详情!






