BP算法全名:(Error) Back Propagation ,中文名:误差反向传播算法
简单来说:
前向传播简要来说就是根据输入,经过权值、激活函数、隐藏层,获得输出。
反向传播就是根据输出,经过与期望值的比较,再通过梯度下降算法求偏导、改变权值,最终修改参数使输出和期望值的差距变到最小。如下图所示。
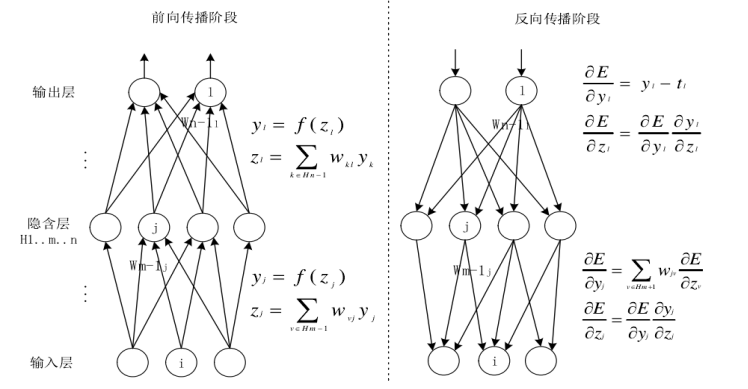
1:前向传播算法
所谓的前向传播算法就是:将上一层的输出作为下一层的输入,并计算下一层的输出,一直到运算到输出层为止。
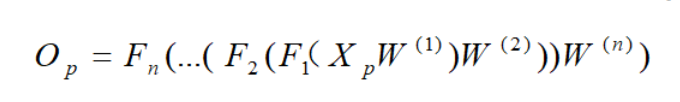
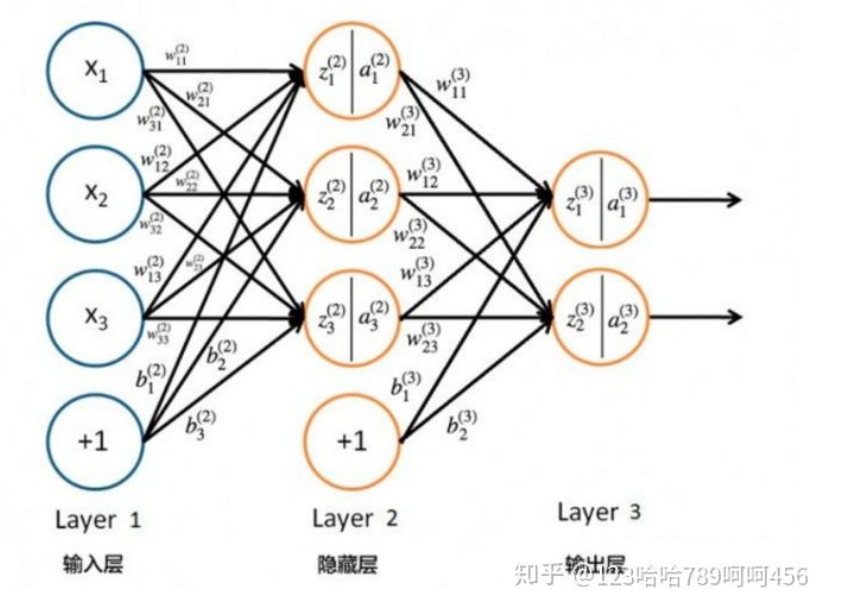
对于Layer 2的输出  ,
, ,
, ,
,



对于Layer 3的输出 ,
,


从上面可以看出,使用代数法一个个的表示输出比较复杂,而如果使用矩阵法则比较的简洁。将上面的例子一般化,并写成矩阵乘法的形式,


其中  为 sigmoid 函数。
为 sigmoid 函数。
这个表示方法就很简洁、很漂亮,后面我们的讨论都会基于上面的这个矩阵法表示来。所以,应该牢牢记住我们符号的含义,否则在后面推导反向传播公式时会比较懵。
2. 反向传播算法(BP算法)
反向传播是一种与最优化方法(如梯度下降法)结合使用的,用来训练人工神经网络的常见方法。该方法对网络中所有权重计算损失函数的梯度。这个梯度会反馈给最优化方法,用来更新权值以最小化损失函数。
梯度下降是优化算法,反向传播是其在神经网络上的具体实现方式
反向传播是链式的梯度下降。
简单介绍一下链式法则:
微积分中的链式法则(为了不与概率中的链式法则相混淆)用于计复合函数的导数。反向传播是一种计算链式法则的算法,使用高效的特定运输顺序。
设  是实数,
是实数,  和
和  是从实数映射到实数的函数。假设
是从实数映射到实数的函数。假设  并且
并且  。那么链式法则就是:
。那么链式法则就是: 。
。
推导BP算法 ( get一下重点内容 )
在进行反向传播算法前,我们需要选择一个损失函数,来度量训练样本计算出的输出和真实的训练样本输出之间的损失。我们使用最常见的均方误差(MSE)来作为损失函数,
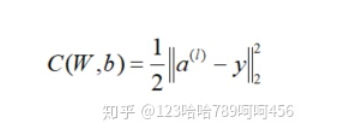
其中  为训练样本计算出的输出,y为训练样本的真实值。加入系数
为训练样本计算出的输出,y为训练样本的真实值。加入系数  是为了抵消微分出来的指数。
是为了抵消微分出来的指数。
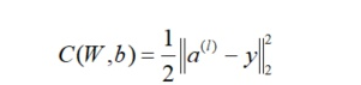
(1) 输出层的梯度


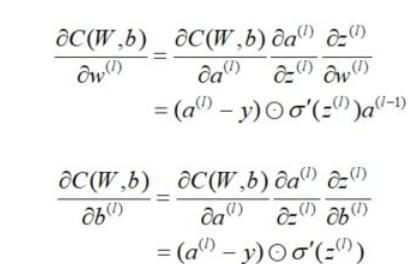
其中  表示Hadamard积,即两个维度相同的矩阵对应元素的乘积。
表示Hadamard积,即两个维度相同的矩阵对应元素的乘积。
我们注意到在求解输出层梯度的时候有公共的部分,记为。
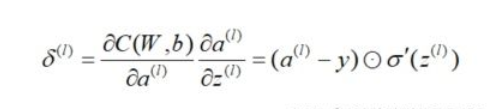
(2) 隐藏层的梯度
我们把输出层  的梯度算出来了 ,那么如何计算
的梯度算出来了 ,那么如何计算  层的梯度,
层的梯度,  层的梯度呢?
层的梯度呢?
因为上面已经求出了输出层的误差,根据误差反向传播的原理,当前层的误差可理解为上一层所有神经元误差的复合函数,即使用上一层的误差来表示当前层误差,并依次递推。
这里我们用数学归纳法,假设第  层的
层的  已经求出,那么我们如何求出第
已经求出,那么我们如何求出第  层的
层的 呢?
呢?
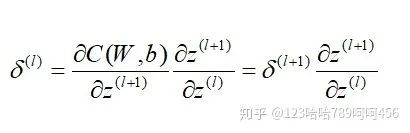
而 和
和 的关系如下:
的关系如下:

这样很容易求出,
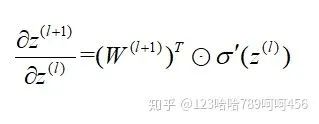
所以,
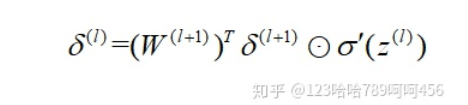
现在我们得到了  的递推关系式,只要求出了某一层的
的递推关系式,只要求出了某一层的 ,求解
,求解 ,
, 的对应梯度就很简单:
的对应梯度就很简单:
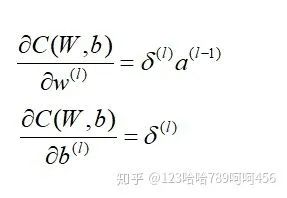
反向传播算法的过程进行一下总结:
输入:总层数L,以及各隐藏层与输出层的神经元个数,激活函数,损失函数,迭代步长  ,最大迭代次数MAX与停止迭代阈值
,最大迭代次数MAX与停止迭代阈值  ,输入的m个训练样本
,输入的m个训练样本 
1. 初始化参数W,b
2. 进行前向传播算法计算,for  to L
to L


3. 通过损失函数计算输出层的梯度
4. 进行反向传播算法计算,for  to 2
to 2
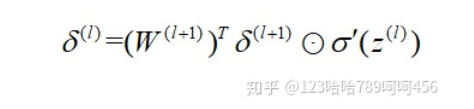
5. 更新W,b
通过梯度下降算法更新权重 和偏置
和偏置 的值,
的值, 为学习率其中
为学习率其中 。
。

6. 如果所有W,b的变化值都小于停止迭代阈值ϵ,则跳出迭代循环
7. 输出各隐藏层与输出层的线性关系系数矩阵W和偏置b。






