前言
之前的文章讲解了关于寻路算法中常见的算法以及AStar寻路算法的原理以及其实现方式，但是对于AStar寻路算法来说，其也有一定的缺点。
A Star算法的问题在于其在进行节点搜索的时候，会把周围8个方向所有的可用邻居节点全部存储于，这样openlist中点的数量会很多，搜索效率较慢，并且占用内存也会很高。
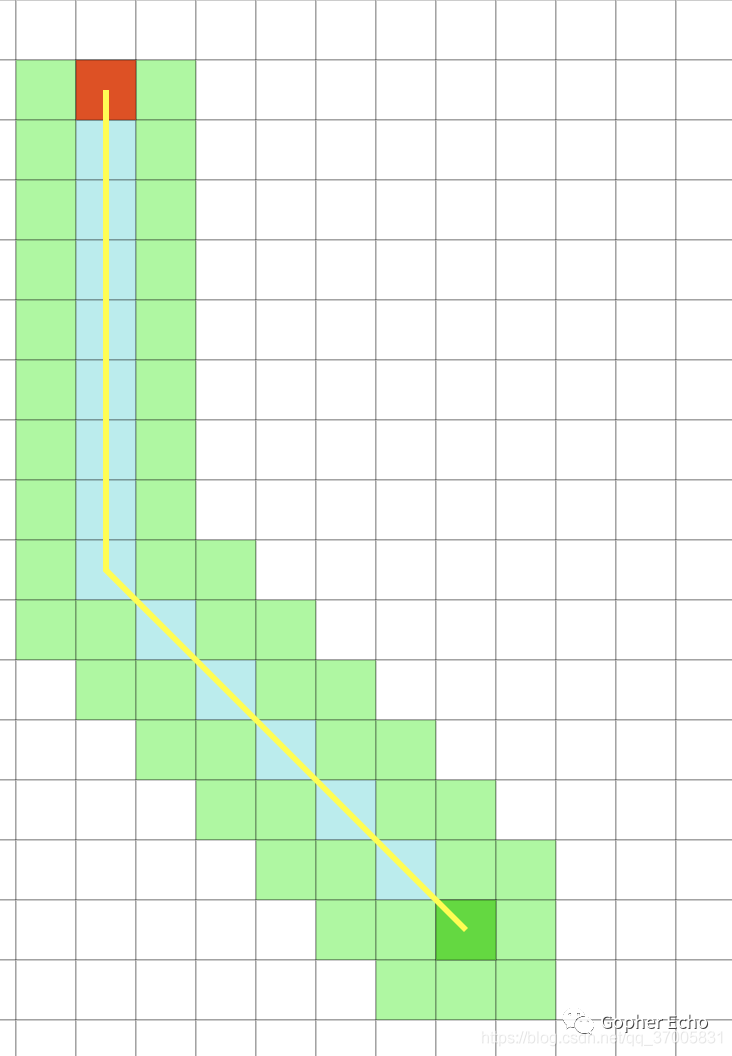如图所示，在无遮挡情况下，可能这种情况会有很多条路径， 对于我们来说只需要一条从起点到终点的路径就够了，下图中绿色为放入OpenList中的节点，由图中看出往往这些节点并没有必要放进去，如果我们把这个图拆分成几段，那么就只需要把每段的起始点放入OpenList中就可以了。
JPS算法
综述
跳点搜索（JPS Jump point search）是对A Star搜索算法的优化。它通过图修剪来减少搜索过程中的对称性，只要满足与网格有关的某些条件，就可以基于关于当前节点邻居的假设来消除网格中的某些节点。该算法可以考虑沿网格中的水平，垂直和对角线的“跳跃”（即一次性跳过几个格子），而不是普通A Star算法考虑的从一个网格位置到下一个网格位置的每个格子。JPS保留了A Star的最优性，同时有可能将其运行时间减少一个数量级[^1]。
如图所示，上图为JPS算法搜索相同路径的结果，从图中可以看出，只有一个蓝色的点被加入到了OpenList中，不同于 A Star算法中直接获取当前节点可用邻居节点来进行拓展搜索的策略，JPS 根据当前节点的前进方向、符合条件的跳点等方式，来进行后续放入OpenList节点的筛选。
强迫邻居（Forced Neighbour）
强迫邻居的概念为：节点 x 的8个邻居中有障碍，且 x 的父节点 p 经过x 到达 n 的距离代价比不经过 x 到达的 n 的任意路径的距离代价小，则称 n 是 x 的强迫邻居[^2]。
这段概念很难理解，作者在学习的时候也很懵😓，我们直接拿图来解释更好一些。
首先要明确一个问题：当前自动寻路的行走方向有8个，如图所示：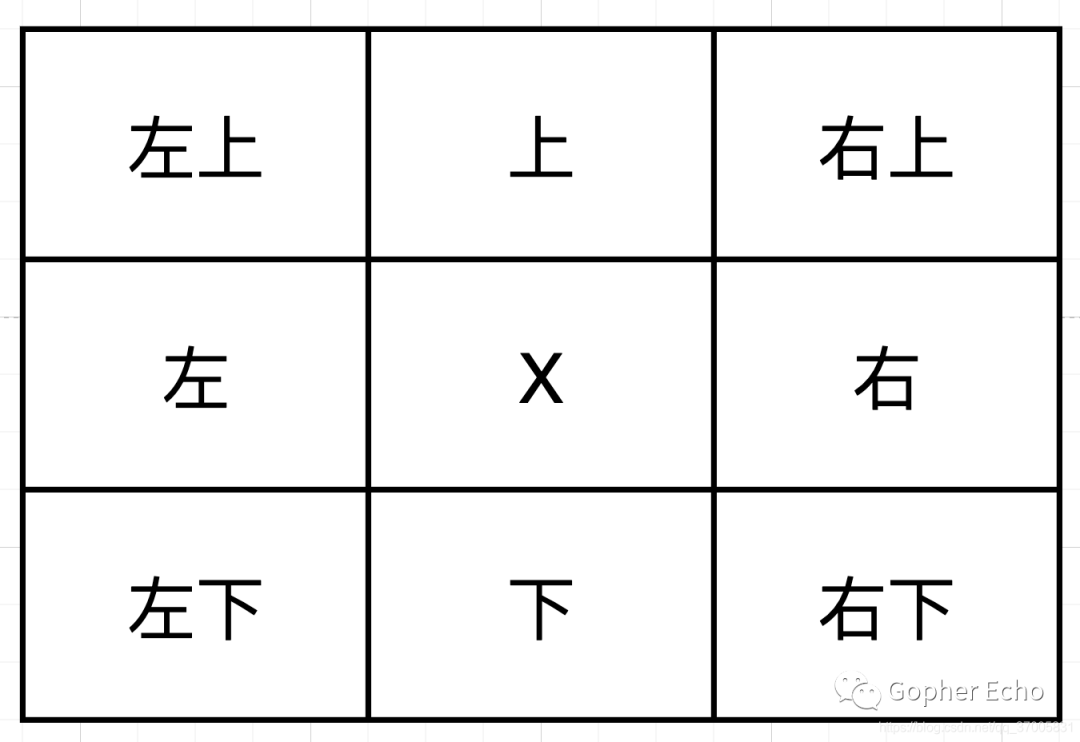
当前节点X有8种前进方向，分别为左上、上、右上、左、右、左下、下、右下，那么对于X来说，其父节点可能在其垂直或者水平方向（上、下、左、右），也有可能在其斜方（左上、右上、左下、右下），如图所示：
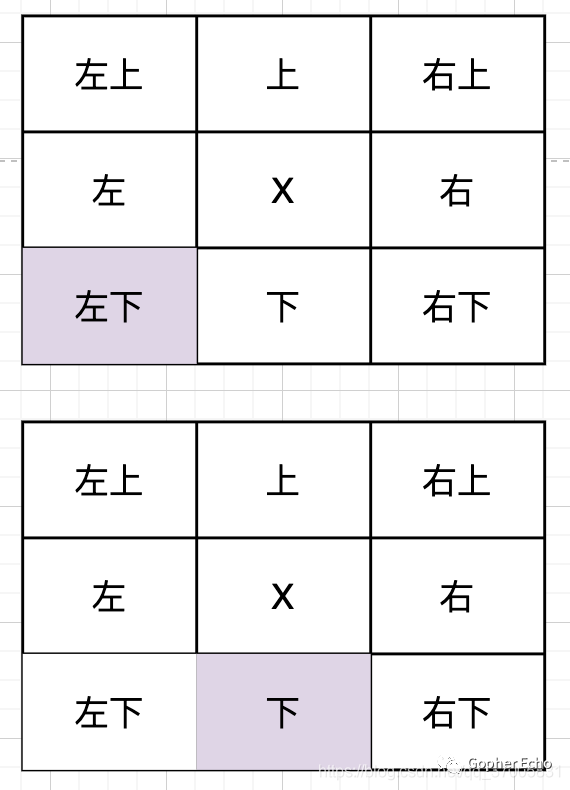
上图所示，紫色方块为节点X的父节点，上图为节点X在其父节点斜方，下图节点X在其父节点的垂直方向，此时我们可以说节点X的前进方向为斜方前进或垂直（水平）前进。
接下来我们分别来讲解在斜方前进或垂直（水平）前进时，强迫邻居的概念（或者可以说如何确定强迫邻居）。
垂直、水平方向强迫邻居的查找
首先来讲一下垂直、水平方向强迫邻居的查找方式，如图所示，深绿色为当前节点位置，黄色的线代表行走方向，红色的点代表终点，当前行走方向为右方，那么此时当前节点位置上方、下方均有阻挡，此时要进行以下逻辑：
1.如果当前节点上方有阻挡，且下一个要到达的节点以及当前节点右上方节点是可用节点（即无阻挡）那么其强迫邻居为当前节点右上方的节点。2.如果当前节点下方有阻挡，且下一个要到达的节点以及当前节点右下方节点是可用节点，那么其强迫邻居为当前节点右下方的节点。3.如果均符合1、2两个条件，那么该节点有两个强迫邻居。
由上述的条件可以举一反三，分别分析出余下三个方向（上、左、下）的强迫邻居条件，即：
1.当前进方向为上（下）方时，判断当前节点左（右）侧是否有阻挡，如有且当前节点前进方向的下一个节点以及当前节点前进方向的左（右）前方均为可用节点时，其当前节点的左（右）前方的节点为强迫邻居。2.当前进方向为左（右）方时，判断当前节点的上（下）侧是否有阻挡，如有则当前节点的前进方向的下一个节点以及当前节点前进方向的上（下）前方均为可用节点时，其当前节点的上（下）前方的节点为强迫邻居。
其实上面的条件简而言之可以理解为，当前节点水平（垂直）侧有阻挡且当前节点的下一个节点和阻挡侧的下一个节点均可用，那么阻挡侧的下一个节点为当前节点的强迫邻居。
斜方强迫邻居的查找
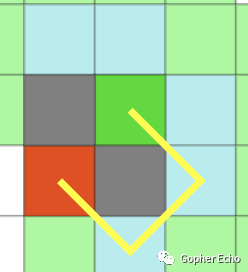
如果当前前进方向为右上方，强迫邻居的寻找方式如图所示（忽略那条线），如图所示，红色点为深绿色点（当前点）的父节点，两个黑色的方块为阻挡，那么强迫邻居的条件如下：
1.如果当前节点左侧有阻挡，且其上方与左上方均为可用节点（即无阻挡），则当前节点的左上方为强迫邻居。2.如果当前节点下方有阻挡，且其右侧与右下方均为可用节点（即无阻挡），则当前节点的右下方为强迫邻居。3.如果1、2条件均符合，则左上方、右下方均为强迫邻居
1.
由上述的条件可以举一反三，分别分析出余下三个方向（左上、左下、右下）的强迫邻居条件，即：
1.
当前进方向为左上方时、若其父节点的上方（左方）有阻挡时，且当前节点的右上方与上方（左方与左下方）均为可用节点时，强迫邻居为右上方（左下方）。按照下图来看。强迫邻居为蓝色节点。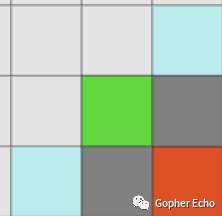
2.
当前进方向为左下方时、若其父节点的左侧（下方）有阻挡时，且当前节点的左上方与左方（下方与右下方）均为可用节点时，强迫邻居为左上方（右下方）。按照下图来看，强迫邻居为蓝色节点。
当前进方向为右下方时、若其父节点的下方（右侧）有阻挡时，且当前节点的下方与左下方（右上方与右方）均为可用节点时，强迫邻居为左下方（右上方）。按照下图来看，强迫邻居为蓝色节点。
跳跃点（Jump Point）
所谓的跳点搜索算法，就是在一次寻路过程中主动寻找障碍，通过障碍的位置计算出：经过障碍代价最小的一些关键位置，并将这些位置中代价最小的点作为下一次寻路过程的起点[^3]。
那么如何确定当前节点是否是跳跃点那么就是一件很重要的事情，如何确定跳点，有以下三个规则：
1.
当前节点是终（起）点。
2.
当前节点至少有一个强迫邻居。
3.如果父节点在斜方，那么当前节点的水平或垂直方向上有满足条件a，b的点。
举个🌰
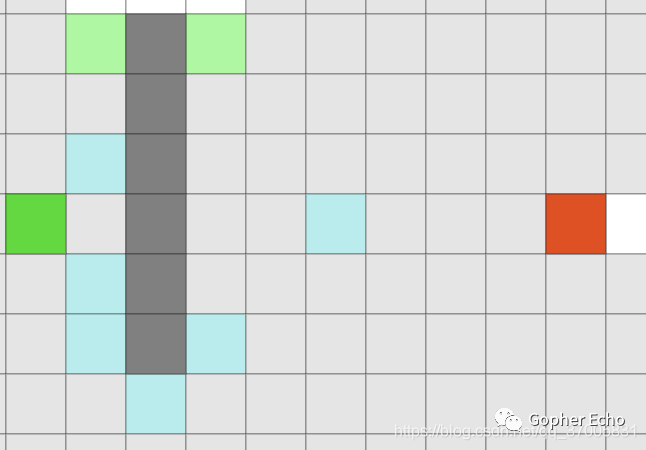上图中绿色点为起点，红色为终点，黑色为障碍，蓝（浅绿）色点为跳点，图中可以看出由多个跳点均可以看出符合上述三个条件的跳点。
搜索过程
讲完了强迫邻居和跳跃点两个重要的概念，那么接下来说一下搜索过程：
1.将开始节点的周围8个可用节点加入OpenList（和 AStar一样）。2.在OpenList里取出一个代价最低的节点，进行如下逻辑判断：
1.如果是终点，则回溯，返回结果。2.如果不是，判断当前行进方向：
1.如果行进方向为水平、垂直方向那么则继续根据其前进方向进行递归搜索，直到遇到以下三个条件后，终止递归搜索
1.当前递归到的节点是不可用节点。2.当前节点超出地图编辑边界。3.当前节点为跳点，此时将当前节点加入到OpenList中并记录其强迫邻居的方向。
2.如果行进方向为斜方，如果当前节点是跳点则搜索结束，否则进行下述操作：
1.如果前进方向为右上方，则根据水平、垂直方向的搜索方式，搜索当前节点的上方以及右方寻找跳点，接着向行进方向递归搜索。搜索方式也为先水平、垂直方向，再斜方。2.如果前进方向为左上方，则根据水平、垂直方向的搜索方式，搜索当前节点的上方以及左方寻找跳点，接着向行进方向递归搜索。搜索方式也为先水平、垂直方向，再斜方。3.如果前进方向为左下方，则根据水平、垂直方向的搜索方式，搜索当前节点的下方以及左方寻找跳点，接着向行进方向递归搜索。搜索方式也为先水平、垂直方向，再斜方。4.如果前进方向为右下方，则根据水平、垂直方向的搜索方式，搜索当前节点的下方以及右方寻找跳点，接着向行进方向递归搜索。搜索方式也为先水平、垂直方向，再斜方。
3.根据当前行进方向搜索完毕后，如果当前节点是跳点，则按照2的方式搜索当前节点的强迫邻居。4.当按照2的方式搜索时，每次递归需要将上一节点当作下一节点的父节点保存起来，以便找到终点的时候方便回溯（这点和A Star是一样的），同时也要计算其Fn值。
网上找了个搜索系列的图，可以作为演示（图侵删）[^2]。
假设起点为绿色节点，终点为红色节点。
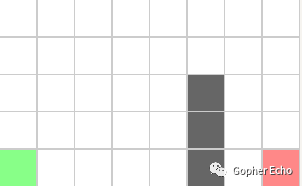
重复直线搜索和斜向搜索过程，斜方向前进了3步。在第3步判断出黄色节点为跳点（依据是水平方向有其它跳点），将黄色跳点放入openlist，然后斜方向搜索完成，绿色节点移除于openlist，放入closelist。
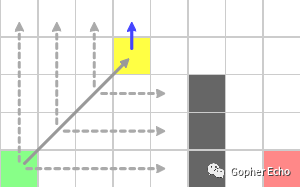
对openlist下一个权值最低的节点（即黄色节点）开启搜索，在直线方向上发现了蓝色节点为跳点（依据是紫色节点为强迫邻居），类似地，放入openlist。
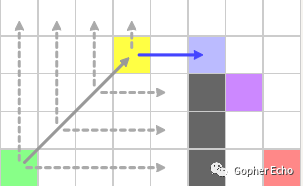
由于斜方向还没结束，继续前进一步。最后一次直线搜索和斜向搜索都碰到了边界，因此黄色节点搜索完成，移除于openlist，放入closelist。
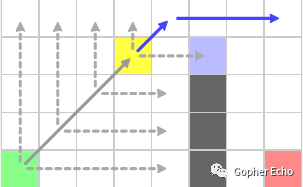
对openlist下一个权值最低的节点（原为蓝色节点，下图变为黄色节点）开启搜索，直线搜索碰到边界，斜向搜索无果。斜方继续前进一步，仍然直线搜索碰到边界，斜向搜索无果。
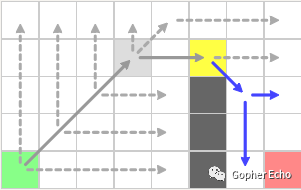
由于斜方向还没结束，继续前进一步。
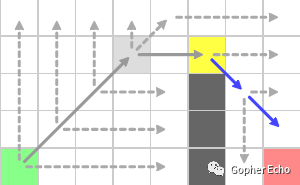
最终在直线方向上发现了红色节点为跳点，因此蓝色节点先被判断为跳点，只添加蓝色节点进openlist。斜方向完成，黄色节点搜索完成。
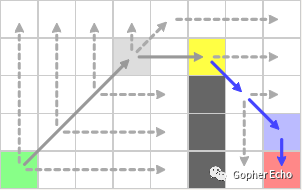
最后openlist取出的蓝色节点开启搜索，在水平方向上发现红色节点，判断为终点，算法完成。
源代码
接下来看一下具体实现，由于没有做优化，仅仅是考虑实现，因此代码可能有一些不合理之处，望见谅。
// 当前进方向为斜方时，要搜索的水平、垂直方位
var diagonalLine = map[tools.Azimuth][2]tools.Azimuth{
tools.RightUp: {tools.Up, tools.Right},
tools.RightDown: {tools.Down, tools.Right},
tools.LeftUp: {tools.Up, tools.Left},
tools.LeftDown: {tools.Down, tools.Left},
}
func (receiver *FindAWay) doJPS(result *[]*tools.Node) {
for {
if receiver.OpenQueue.Len() <= 0 {
break
}
// 在OpenList里获取损耗最低的节点
curNode := receiver.openGet()
// 判断是否是终点
if receiver.end.Equal(curNode.Position()) {
// 是的话回溯
receiver.statistics(curNode, result)
return
}
// 判断是否在CloseList
if _, ok := receiver.CloseMap[curNode.Position()]; ok {
continue
}
// 加入Close List 防止重复扫描
receiver.closePut(curNode)
// 寻找跳点
receiver.findJumpPoint(curNode)
}
}
func (receiver *FindAWay) findJumpPoint(cur *tools.Node) {
switch cur.ParentAzimuth() {
case tools.LeftUp, tools.RightUp, tools.LeftDown, tools.RightDown:
// 前进方向为斜方则进行斜方搜索
receiver.sSearch(cur)
// 搜索当前节点的强迫邻居
receiver.rangeForcedNeighbours(cur)
default:
// 水平、垂直方向来的直接拿到其下一个节点
nextNode := tools.GlobalMap.GetNode(tools.NodeFormula[cur.ParentAzimuth()](cur.Position()))
if nextNode == nil {
return
}
nextNode.SetParent(cur)
nextNode.SetParentAzimuth(cur.ParentAzimuth())
nextNode.CalcHn(receiver.end.Position()).CalcGn(tools.HVCost).CalcFn()
// 水平垂直搜索
receiver.hvSearch(nextNode)
// 搜索当前节点的强迫邻居
receiver.rangeForcedNeighbours(cur)
}
}
func (receiver *FindAWay) rangeForcedNeighbours(cur *tools.Node) {
// 这个切片存储的是如果当前节点有强迫邻居，则存储其强迫邻居的方位
if len(cur.ForcedNeighbourAzimuth()) > 0 {
for _, azimuth := range cur.ForcedNeighbourAzimuth() {
nextNode := tools.GlobalMap.GetNode(tools.NodeFormula[azimuth](cur.Position()))
if nextNode == nil {
return
}
nextNode.SetParent(cur)
nextNode.SetParentAzimuth(azimuth)
nextNode.CalcHn(receiver.end.Position()).CalcGn(tools.SCost).CalcFn()
// 搜索其强迫邻居
receiver.sSearch(nextNode)
}
}
}
// 水平、垂直搜索
func (receiver *FindAWay) hvSearch(cur *tools.Node) {
// 节点无效。终止
if !cur.EffectiveCoordinate() {
return
}
// 判断是否是跳点
have := receiver.isJumpPoint(cur)
if _, ok := receiver.CloseMap[cur.Position()]; !ok && have {
// 放入OpenList
receiver.openPut(cur)
return
}
nextNode := tools.GlobalMap.GetNode(tools.NodeFormula[cur.ParentAzimuth()](cur.Position()))
if nextNode == nil {
return
}
nextNode.SetParent(cur)
nextNode.SetParentAzimuth(cur.ParentAzimuth())
nextNode.CalcHn(receiver.end.Position()).CalcGn(tools.HVCost).CalcFn()
// 递归
receiver.hvSearch(nextNode)
}
// 斜方搜索
func (receiver *FindAWay) sSearch(cur *tools.Node) {
if !cur.EffectiveCoordinate() {
return
}
have := receiver.isJumpPoint(cur)
if _, ok := receiver.CloseMap[cur.Position()]; !ok && have {
receiver.openPut(cur)
return
}
oldA := cur.ParentAzimuth()
defer cur.SetParentAzimuth(oldA)
azimuths := diagonalLine[cur.ParentAzimuth()]
// 先垂直搜索
cur.SetParentAzimuth(azimuths[0])
receiver.hvSearch(cur)
//再水平搜索
cur.SetParentAzimuth(azimuths[1])
receiver.hvSearch(cur)
nextNode := tools.GlobalMap.GetNode(tools.NodeFormula[oldA](cur.Position()))
if nextNode == nil {
return
}
nextNode.SetParent(cur)
nextNode.SetParentAzimuth(oldA)
nextNode.CalcHn(receiver.end.Position()).CalcGn(tools.SCost).CalcFn()
// 再斜方递归下去
receiver.sSearch(nextNode)
}
func (receiver *FindAWay) isJumpPoint(cur *tools.Node) bool {
// 当前点为end 则是跳点
if receiver.end.Equal(cur.Position()) {
return true
}
switch cur.ParentAzimuth() {
// 斜方过来的 则看看垂直、水平方有没有跳点
case tools.LeftUp, tools.RightUp, tools.LeftDown, tools.RightDown:
oldA := cur.ParentAzimuth()
azimuths := diagonalLine[cur.ParentAzimuth()]
cur.SetParentAzimuth(azimuths[0])
haveJp := receiver.findForcedNeighbour(cur)
cur.SetParentAzimuth(azimuths[1])
haveJp = receiver.findForcedNeighbour(cur)
cur.SetParentAzimuth(oldA)
return haveJp
default:
return receiver.findForcedNeighbour(cur)
}
}
func (receiver *FindAWay) findForcedNeighbour(node *tools.Node) bool {
// 如果前进方向侧方没有阻挡则必定无强迫邻居
// 前进方向为上、下时，侧方为左、右
// 前进方向为左、右时，侧方为上、下
switch node.ParentAzimuth() {
case tools.Up, tools.Down:
if tools.GlobalMap.EffectiveCoordinate(tools.NodeFormula[tools.Left](node.Position())) &&
tools.GlobalMap.EffectiveCoordinate(tools.NodeFormula[tools.Right](node.Position())) {
return false
}
case tools.Left, tools.Right:
if tools.GlobalMap.EffectiveCoordinate(tools.NodeFormula[tools.Up](node.Position())) &&
tools.GlobalMap.EffectiveCoordinate(tools.NodeFormula[tools.Down](node.Position())) {
return false
}
default:
return false
}
have := false
switch node.ParentAzimuth() {
case tools.Right:
// 1：上侧有阻挡且右上侧可走
// 2：下侧有阻挡 右下侧可走
// 3: 右上、右下其中一点为终点
// 二者符合其一则代表有强迫邻居
if (!tools.GlobalMap.EffectiveCoordinate(tools.NodeFormula[tools.Up](node.Position())) &&
tools.GlobalMap.EffectiveCoordinate(tools.NodeFormula[tools.RightUp](node.Position()))) ||
receiver.end.EqualIJ(tools.NodeFormula[tools.RightUp](node.Position())) {
node.AddForcedNeighbourAzimuth(tools.RightUp)
have = true
}
if (!tools.GlobalMap.EffectiveCoordinate(tools.NodeFormula[tools.Down](node.Position())) &&
tools.GlobalMap.EffectiveCoordinate(tools.NodeFormula[tools.RightDown](node.Position()))) ||
receiver.end.EqualIJ(tools.NodeFormula[tools.RightDown](node.Position())) {
node.AddForcedNeighbourAzimuth(tools.RightDown)
have = true
}
case tools.Left:
// 1：上侧有阻挡且左上侧可走
// 2：下侧有阻挡且左下侧可走
// 3: 左上、左下其中一点为终点
// 二者符合其一则代表有强迫邻居
if (!tools.GlobalMap.EffectiveCoordinate(tools.NodeFormula[tools.Up](node.Position())) &&
tools.GlobalMap.EffectiveCoordinate(tools.NodeFormula[tools.LeftUp](node.Position()))) ||
receiver.end.EqualIJ(tools.NodeFormula[tools.LeftUp](node.Position())) {
node.AddForcedNeighbourAzimuth(tools.LeftUp)
have = true
}
if (!tools.GlobalMap.EffectiveCoordinate(tools.NodeFormula[tools.Down](node.Position())) &&
tools.GlobalMap.EffectiveCoordinate(tools.NodeFormula[tools.LeftDown](node.Position()))) ||
receiver.end.EqualIJ(tools.NodeFormula[tools.LeftDown](node.Position())) {
node.AddForcedNeighbourAzimuth(tools.LeftDown)
have = true
}
case tools.Up:
// 1：左侧有阻挡且左上侧可走
// 2：右侧有阻挡且右上侧可走
// 3: 左上、右上其中一点为终点
// 二者符合其一则代表有强迫邻居
if (!tools.GlobalMap.EffectiveCoordinate(tools.NodeFormula[tools.Left](node.Position())) &&
tools.GlobalMap.EffectiveCoordinate(tools.NodeFormula[tools.LeftUp](node.Position()))) ||
receiver.end.EqualIJ(tools.NodeFormula[tools.LeftUp](node.Position())) {
node.AddForcedNeighbourAzimuth(tools.LeftUp)
have = true
}
if (!tools.GlobalMap.EffectiveCoordinate(tools.NodeFormula[tools.Right](node.Position())) &&
tools.GlobalMap.EffectiveCoordinate(tools.NodeFormula[tools.RightUp](node.Position()))) ||
receiver.end.EqualIJ(tools.NodeFormula[tools.RightUp](node.Position())) {
node.AddForcedNeighbourAzimuth(tools.RightUp)
have = true
}
case tools.Down:
// 1：左侧有阻挡且左下侧可走
// 2：右侧有阻挡且右下侧可走
// 3: 左下、右下其中一点为终点
// 二者符合其一则代表有强迫邻居
if (!tools.GlobalMap.EffectiveCoordinate(tools.NodeFormula[tools.Left](node.Position())) &&
tools.GlobalMap.EffectiveCoordinate(tools.NodeFormula[tools.LeftDown](node.Position()))) ||
receiver.end.EqualIJ(tools.NodeFormula[tools.LeftDown](node.Position())) {
node.AddForcedNeighbourAzimuth(tools.LeftDown)
have = true
}
if (!tools.GlobalMap.EffectiveCoordinate(tools.NodeFormula[tools.Right](node.Position())) &&
tools.GlobalMap.EffectiveCoordinate(tools.NodeFormula[tools.RightDown](node.Position()))) ||
receiver.end.EqualIJ(tools.NodeFormula[tools.RightDown](node.Position())) {
node.AddForcedNeighbourAzimuth(tools.RightDown)
have = true
}
default:
}
return have
}复制
总结
和A Star算法相比，JPS的优缺点为：
1.使用JPS算法比A*更快（绝大部分地图），内存占用更小，因为OpenList少了很多节点（最差的情况和A Star一样，最差的是每个障碍都不连续，中间都有缝隙，这样所有地方都是跳点了）2.只适用于网格节点类型，不支持Navmesh或者路径点寻路方式。3.当地图很大时，水平、垂直方向的递归深度会很深。
参考资料
[^1]: Jump point search https://en.wikipedia.org/wiki/Jump_point_search
[^2]: JPS/JPS+ 寻路算法 https://www.cnblogs.com/KillerAery/archive/2020/06/17/12242445.html
[^3]: JPS寻路算法 https://www.jianshu.com/p/9335dddb04b4
