系列文章导图:
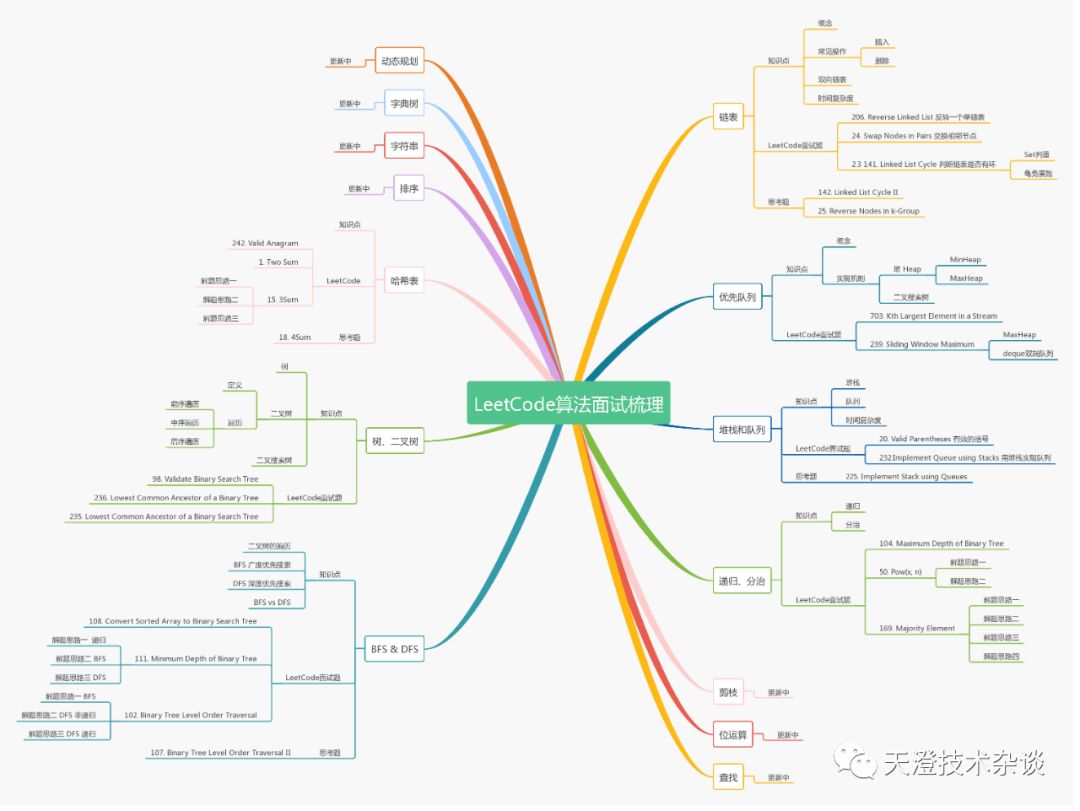
全部系列文章请点击阅读原文
1. 知识点
1.1 二叉树的遍历
1.2 BFS 广度优先搜索
1.3 DFS 深度优先搜索
1.4 BFS vs DFS
2. 题目
2.1 108. Convert Sorted Array to Binary Search Tree
2.2 111. Minimum Depth of Binary Tree
2.2.1 解题思路一: 递归
2.2.2 解题思路二: DFS
2.2.3 解题思路三: BFS
2.2.4 思考题
2.3 102. Binary Tree Level Order Traversal
2.3.1 解题思路一: BFS
2.3.2 解题思路二: DFS非递归实现
2.3.3 解题思路三: DFS递归实现
2.3.4 思考题
1. 知识点
本章节重点介绍二叉树的广度和深度优先搜索。
1.1 二叉树的遍历
前序遍历、中序遍历、后序遍历在之前将二叉树的时候已经提到过,这里不再重复,需要再次了解的请看下面链接。
二叉树的遍历
1.2 BFS 广度优先搜索
下面介绍一下BFS,即广度优先搜索,下面图解示例看BFS是如何遍历的:
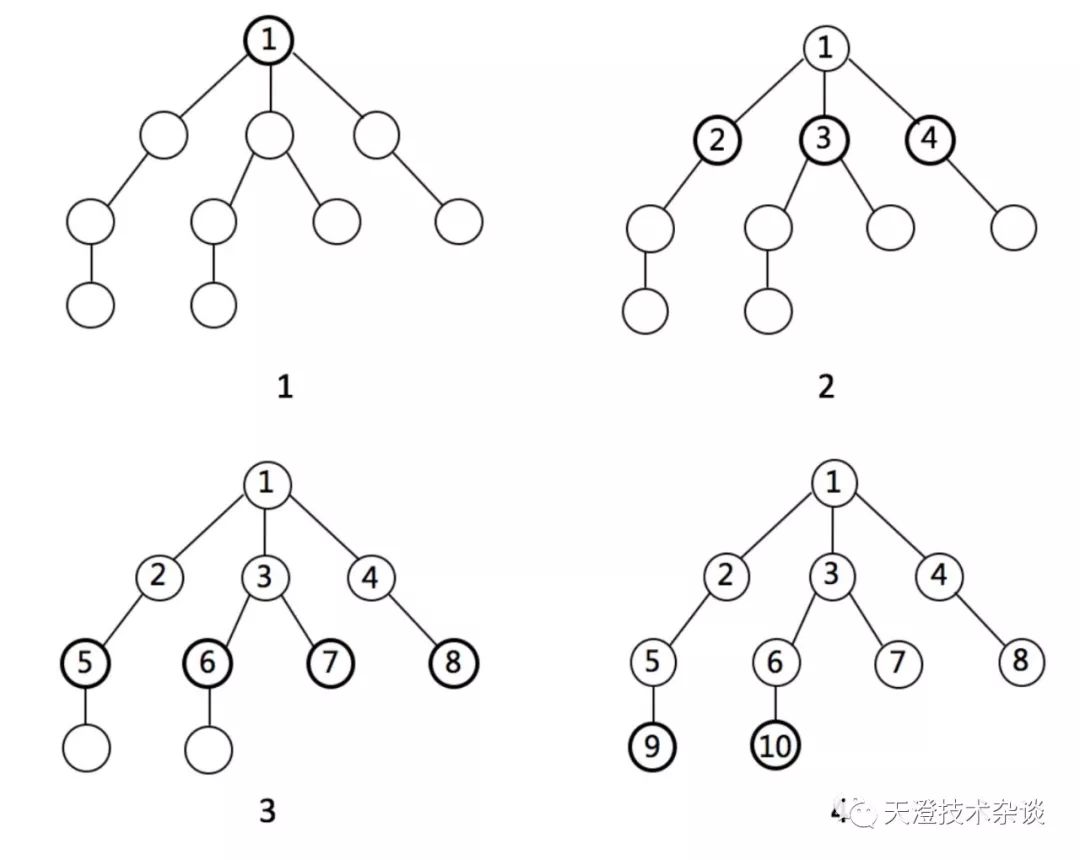
上面四幅图,1-2-3-4,比较清晰的描述了BFS的是如何遍历的,可以理解为是按层进行扫荡。
1.3 DFS 深度优先搜索
跟BFS一样,同样给出图解示例,带大家理解DFS的遍历过程:
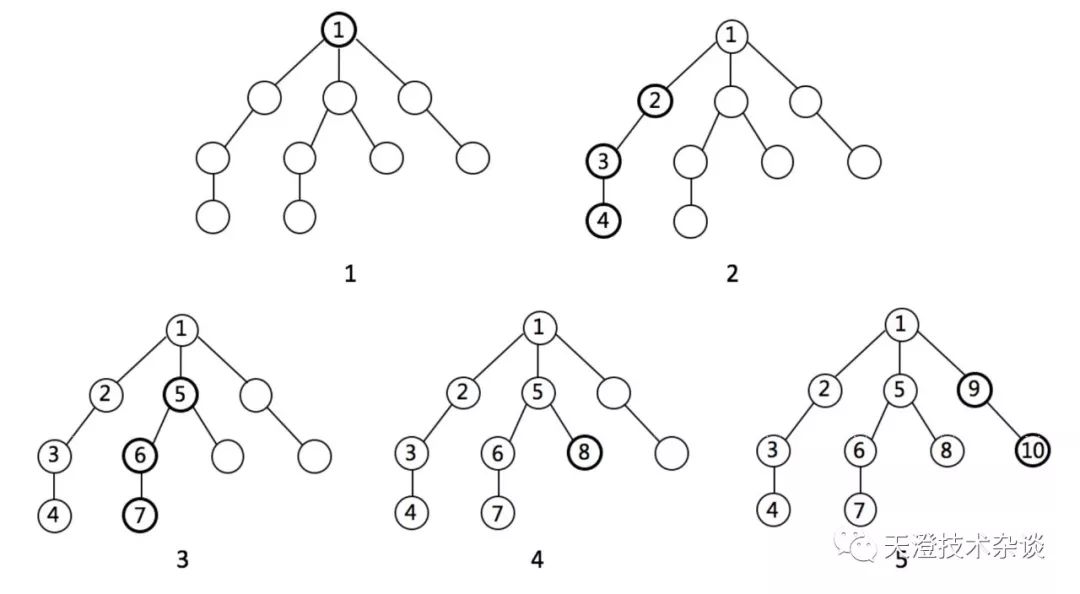
可以看出DFS,是一般先遍历左子树,并且将左子树的子孙全部遍历完,直到叶子节点,然后回到根节点,继续遍历右子树。
1.4 BFS vs DFS
根据上面对BFS和DFS的介绍,给出一张直观图来对比二者的区别:
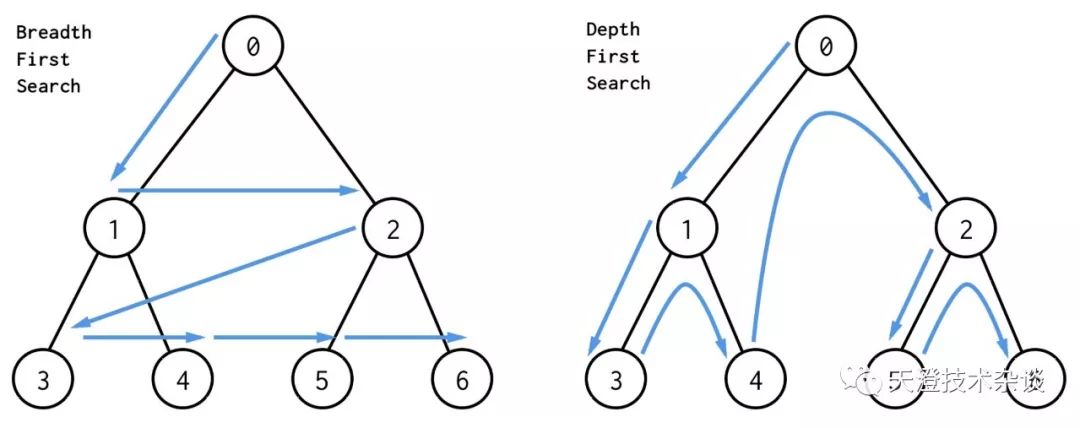
2. 题目
2.1 108. Convert Sorted Array to Binary Search Tree
题目要求
将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树。Example
Given the sorted array: [-10,-3,0,5,9],
One possible answer is: [0,-3,9,-10,null,5], which represents the following height balanced BST:
0
/ \
-3 9
/ /
-10 5
解题思路
这题目主要考察对二叉搜索树的了解以及中序遍历的知识点。
容易想到和理解的一条思路,就是利用二叉搜索树按中序遍历是有序的特性。而中序遍历的规则是 左-根-右。即数组的中间值则是根节点,左右两边则分别是左子树和右子树,按递归的思维,左子树和右子树也按照上面的逻辑进行树的转换。代码演示
class Solution(object):
def sortedArrayToBST(self, nums):
"""
:type nums: List[int]
:rtype: TreeNode
"""
if len(nums) == 0:
return None
mid = int(len(nums) / 2)
root = TreeNode(nums[mid])
root.left = self.sortedArrayToBST(nums[:mid])
root.right = self.sortedArrayToBST(nums[mid + 1:])
return root
2.2 111. Minimum Depth of Binary Tree
题目要求
Given a binary tree, find its minimum depth.找出二叉树的最小深度。Example
Given binary tree [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
return its minimum depth = 2.
2.2.1 解题思路一: 递归
思路
上一篇讲了二叉树的最高的深度,用的就是递归思维,所以找出二叉树的最小深度,我们先来用递归解题,思路就是递归查找左子树和右子树的深度,然后取二者的小者即可。代码演示
class Solution(object):
def minDepth(self, root):
"""
:type root: TreeNode
:rtype: int
"""
if not root:
return 0
if root.left is None:
return self.minDepth(root.right) + 1
if root.right is None:
return self.minDepth(root.left) + 1
left = self.minDepth(root.right) + 1
right = self.minDepth(root.left) + 1
return min(left, right)
代码也比较清晰,可以跟找出二叉树的最大深度进行对比。也就是分别找出左子树和右子树的深度,取小者返回即可。
时间复杂度O(N)
2.2.2 解题思路二: DFS
思路
思路二则采用今天的主题,DFS来解,按照知识点的描述,DFS是先将左子树的自身遍历完毕,再回来遍历右子树。DFS非递归解法一般需要采用栈Stack数据结构,按层将右子树和左子树依次入栈,下一次先出左子树(后入),然后进行下一轮,判断左子树的子孙,直到左子树遍历完毕,获取到左子树的最高深度;右子树也是如此。如果该节点是叶子节点,则说明已经到底,将此深度与最小深度进行比较。代码演示
class Solution(object):
def minDepth(self, root):
"""
:type root: TreeNode
:rtype: int
DFS O(n)
"""
if not root:
return 0
stack = [(root, 1)]
min_depth = float("inf")
while stack:
cur_node, cur_depth = stack.pop()
children = [cur_node.right, cur_node.left]
if not any(children):
min_depth = min(min_depth, cur_depth)
for child in children:
if not child:
continue
stack.append((child, cur_depth + 1))
return min_depth
先定义一个min_depth,初始化为正无穷,python里正无穷的表达方式是float("inf")。然后检查该节点是否是叶子节点,any([])是表示该数组中是否全为空,如果是则返回True,否则返回False。如果左节点和右节点全为空,则表示是叶子节点,则取该深度与最小深度的小者。然后按先右后左的顺序依次入栈即可。
时间复杂度O(N)
2.2.3 解题思路三: BFS
思路
思路三采用BFS,逐层扫荡二叉树,BFS在此题中,还有一点优势是如果发现某一层出现叶子节点,则直接返回此节点所处的深度就是答案,因为逐层扫荡下去,最先出现叶子节点的层肯定也是深度最小,肯定越往下深度越高。BFS非递归解法则需要借助双端队列的数据结构,因为需要从首边出,尾部进,满足先进先出的特点。代码演示
from collections import deque
class Solution3(object):
def minDepth(self, root):
"""
:type root: TreeNode
:rtype: int
BFS O(n)
"""
if not root:
return 0
queue = deque([(root, 1)])
while queue:
cur_node, cur_depth = queue.popleft()
children = [cur_node.left, cur_node.right]
if not any(children):
return cur_depth
for child in children:
if not child:
continue
queue.append((child, cur_depth + 1))
deque则是Python中双端队列的实现。也是先检查该节点是否是叶子节点,如果是则直接返回结果,否则进行将下一层的左右节点分别入队列
时间复杂度 O(n)
2.2.4 思考题
尝试将上一篇中求二叉树的最高深度,leetcode第104题,也按照DFS和BFS的思路进行求解。如果能自由的写出来,说明你已经掌握DFS和BFS了。
2.3 102. Binary Tree Level Order Traversal
题目要求
Given a binary tree, return the level order traversal of its nodes' values. (ie, from left to right, level by level).
给定一颗二叉树,按层进行遍历,要求先左后右.Example
Given binary tree [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
return its level order traversal as:
[
[3],
[9,20],
[15,7]
]
2.3.1 解题思路一: BFS
思路
按层进行遍历,不就是BFS的特性嘛,所以最直接解法就是BFS了,上面题目已经讲解了BFS是如何实现,接下来看代码讲解.代码演示
from collections import deque
class Solution(object):
def levelOrder(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
BFS
"""
if not root:
return []
queue = deque([root])
result = []
while queue:
cur_level = []
for _ in range(len(queue)):
cur_node = queue.popleft()
cur_level.append(cur_node.val)
if cur_node.left:
queue.append(cur_node.left)
if cur_node.right:
queue.append(cur_node.right)
result.append(cur_level)
return result
BFS非递归实现,首先初始化双端队列,然后判断一层的节点个数,循环每一个节点,进行遍历,同时将每一个节点的孩子进入队列,进行下一轮遍历。
2.3.2 解题思路二: DFS非递归实现
思路
如果此题按DFS是否可以实现了?答案肯定是可以的,麻烦在于需要记住每一层的level,这样遍历左子树后,遍历右子树时需要找到所属的层数。即需要知道每一个节点所属哪一层。代码实现
class Solution(object):
def levelOrder(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
DFS
"""
if not root:
return []
stack, result = [], []
stack.append((root, 0))
while stack:
cur_node, level = stack.pop()
if len(result) < level + 1:
result.append([])
result[level].append(cur_node.val)
children = [cur_node.right, cur_node.left]
if not any(children):
continue
for child in children:
if not child:
continue
stack.append((child, level + 1))
return result
DFS非递归实现采用栈,栈中的元素是一个元组,第一个元素是节点,第二个元素是元素的层数,这样遍历到该节点时,可以将该节点的值放入所属的层次的数组中。
需要注意的是孩子们的压栈顺序是先右孩子再左孩子,因为需要先遍历左孩子,后进先出。
2.3.3 解题思路三: DFS递归实现
DFS这里演示如何使用递归实现,思路跟解题思路二一致。
代码演示
class Solution(object):
def levelOrder(self, root):
"""
:type root: TreeNode
:rtype: List[List[int]]
DFS
"""
if not root:
return []
self.result = []
self.dfs(root, 0)
return self.result
def dfs(self, node, level):
if not node:
return
if len(self.result) < level + 1:
self.result.append([])
self.result[level].append(node.val)
self.dfs(node.left, level + 1)
self.dfs(node.right, level + 1)
这里需要借助一个函数dfs,传入2个参数,一个是节点,一个是节点所属的层数,这样可以知道该节点的值该加入哪一层。
2.3.4 思考题
leetcode 第107题,是该题的变种:107. Binary Tree Level Order Traversal II
Example:
Given binary tree [3,9,20,null,null,15,7],
3
/ \
9 20
/ \
15 7
return its bottom-up level order traversal as:
[
[15,7],
[9,20],
[3]
]
从底部按层遍历,解题思路也是DFS和BFS,欢迎大家在评论区交流。
可以看出DFS和BFS的解题思路是可以复制的,基本都是这个套路,如果你以完全理解,则相关题目是完全难不倒你。
全部系列文章请点击阅读原文。






