机器学习之线性代数：向量的线性生成集与线性无关

我们知道在n维空间内，n个标准单位向量构成的向量组，可以生成整个n维向量空间。例如集合S内的向量组会生成整个三维向量空间。

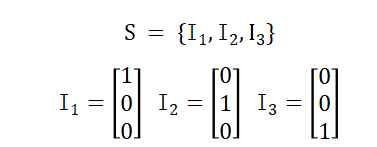
设集合S为n维向量空间的非空子集：

其中A(1)，A(2)，……，A(k)是n维空间内的向量，k是大于n或小于n的正整数，若把X作为集合S内向量通过线性组合生成的向量集合，则：

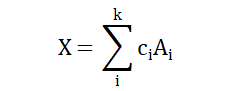
其中c(i)为纯量，也称为系数，它可以取任何实数，A(i)为集合S内的向量，S通过线性组合生成X，则X称为S的线性生成集，若X=R^n，则X为整个n维向量空间。

若c(i)都取实数0，S生成的向量称为零向量，记作0。零向量的模长为0，零向量有下面的性质：

（1）零向量的方向不确定；

（2）零向量的方向与任一向量平行；

（3）与任意向量共线，

（4）与任意向量垂直。

若c(i)都取实数0，是S生成零向量的唯一方式，则S集合内的向量组为线性无关，否则为线性相关。

判断一组向量是否线性相关或线性无关，还有一种判断方式。

当向量组中的任意一个向量都不能用组中有限个向量的线性组合所表示，就说这组向量是线性无关的，反之就是线性相关的。

例如有下面的一组向量：

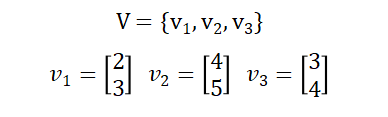
v1、v2和v3看起来是线性无关的，其中任意一个向量无论如何进行数乘，都无法表示另一个向量。但线性组合不仅仅包括数乘，还包括向量的加法。

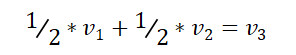
从上面的线性组合可以看出，v3是v1和v2的线性组合，因此V组向量是线性相关的，在这组向量中，v3是多余的向量，因为v3可以由v1和v2的线性组合表示。

实际上集合V内的向量在系数都不为零的情况下，完全可以生成零向量。只要下面的方程成立，集合V内的向量组就是线性相关的。

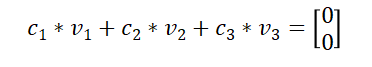
要求出c(1)、c(2)和c(3)，将已知向量代入上面的线性组合：

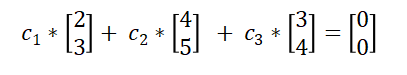
解方程组得：

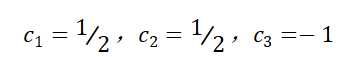
当系数c(i)取上述实数时，方程成立。因此V集合内的向量组是线性相关的。