1. 面积和行列式
1.1 理解行列式
1.1.1 行列式的几何定义
在二维空间中,当我们进行线性变换,也就是对空间坐标进行挤压时,任一形状的面积也会随之改变,并且在此空间坐标中所有面积的缩放比例都是一致的。而这个线性变换前后对面积的缩放比例,被称为这个线性变换的行列式(The determinant of a transformation)。
1.1.2 行列式是否为0
即,如果一个线性变换的行列式是3,则这个线性变换把任一面积改变为原来的三倍。如果一个线性变换的行列式是0,说明它把整个平面压缩至一条线或一点上。
所以,通过判断行列式是否为0,我们可以了解矩阵代表的变换是否将空间压缩至更小的维度上。
1.1.3 行列式与空间定向(orientation of space )
有些变换感觉像是对空间进行了翻转,这就是空间定向的改变(inverted)。从向量角度来说,原先的坐标中,基向量位于的右边,但在变换后,向量位于右边的位置。

当空间定向被改变的时候,行列式为负值。
1.1.4 三维空间的行列式
在三维空间中,行列式代表了变换前后的体积变化。
行列式为0意味着空间被压缩成0体积的东西,在这种情况下,矩阵的列向量必然存在线性相关。
判断三维空间的定向是否变换,即行列式是否为负,可以用右手定则。
1.2 行列式的计算
1.2.1 行列式计算公式:
1.2.2 行列式计算公式的直观理解
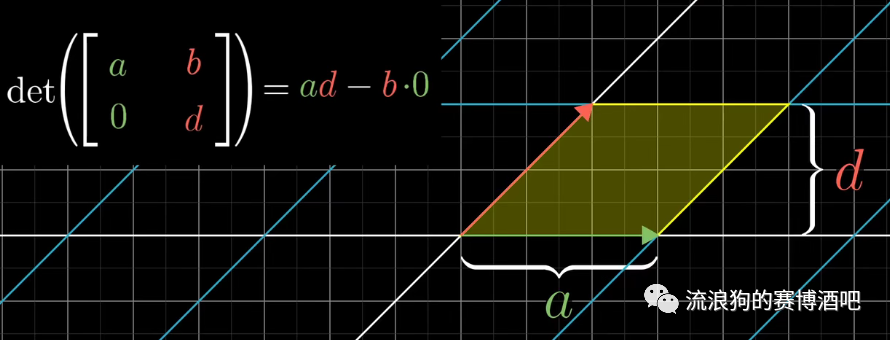
先令公式中b=0 && c=0。此时矩阵相当于把拉长为a倍,拉长为d倍,所以变换后的面积变化为之前的ad倍。

如果仅有c=0而b不为0,那么原先基向量构成的单位为1的正方形在面积变为ad之后,形状也会发生改变(因为向量在横轴上偏移了b个单位。
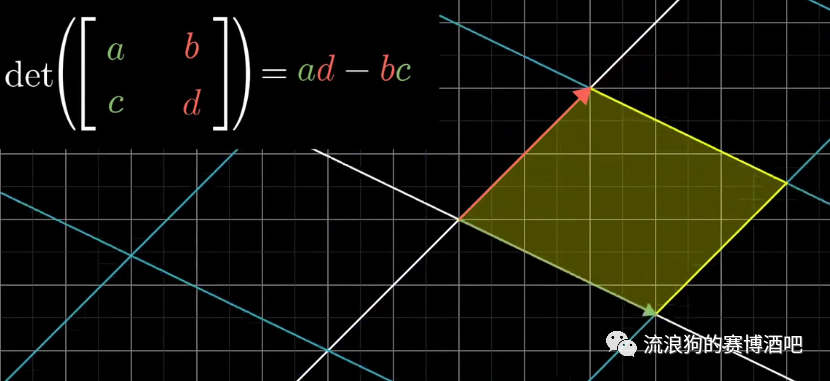
如果b和c都不为0,那么形状和大小均发生变化,并且bc项代表了这个平行四边形在对角方向上的拉伸/压缩幅度。
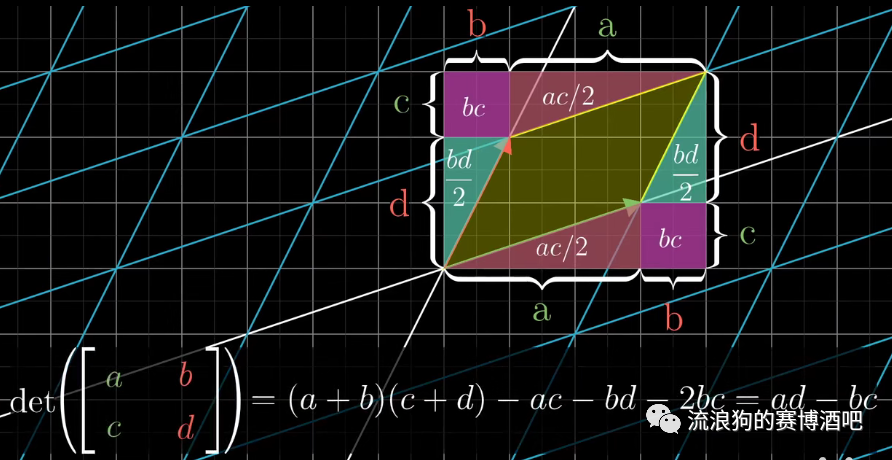
根据abcd四个数值,我们就可以计算出面积改变的精确数值
2. 逆矩阵
2.1 线性方程组
线性方程组(Linear system of equations)有以下两个特征:
未知量仅具有常系数
未知量之间仅进行加和
通常写为这种形式:
2.2 线性方程组与线性变换
线性方程组可以写成
【一个常系数组成的矩阵A】 x【一个未知向量】=【一个常数向量】
的矩阵向量乘法形式。
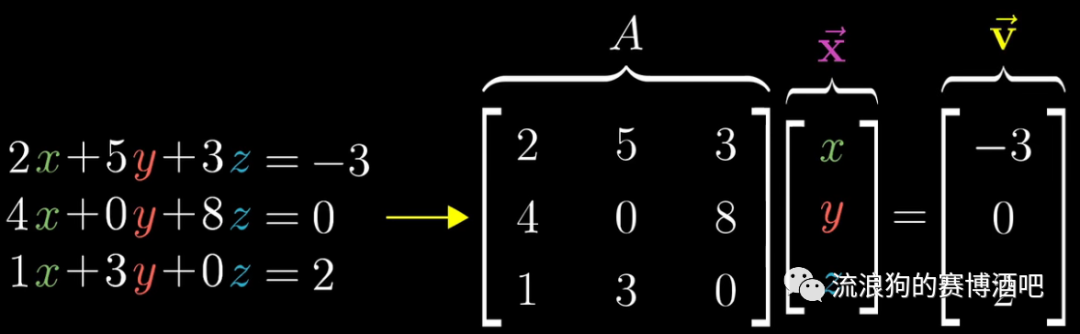
并且,这个等式具有具体的几何含义。由于矩阵A可以代表一种线性变换,所以求解A=意味着我们寻找一个向量,使它在特定线性变换后与重合。
2.3 逆矩阵
当A的行列式不为0,即A所代表的线性变换不会将空间维度压缩时,只要我们逆向对向量进行线性变换,就可以求解出向量的值。
这种逆向的线性变换,通常被称为A的逆(the inverse of A),记为。是空间中唯一一个能还原A所代表的线性变换的矩阵。也就是说,A的逆乘以A等于一个恒等变换(identity transformation),即什么都不做。用公式可以表达为:
上文所说的线性变换公式A=,两边同时乘以A逆可以得到
因为相当于什么都没有做,所以可以省去,上式遂简化为
2.4 行列式与逆矩阵
2.4.1 时,存在唯一
因为在的情况下,也就是线性变换A不会将空间压缩为更低维度时,存在是的唯一逆矩阵,这也意味着线性方程组中,只要未知数的个数与方程组个数一致,我们就可以求得这个方程组的唯一解。
2.4.2 时,不存在
在的情况下,线性变换将空间压缩到了更低维度,这时便不存在。因为如果要解压缩维度,必然会使一个向量映射为多个向量(一个终点变为一条直线),而函数只能完成一对一的映射。
但此时依然可能有解,那就是当正好位于A把平面压缩后形成的那条直线上的时候。
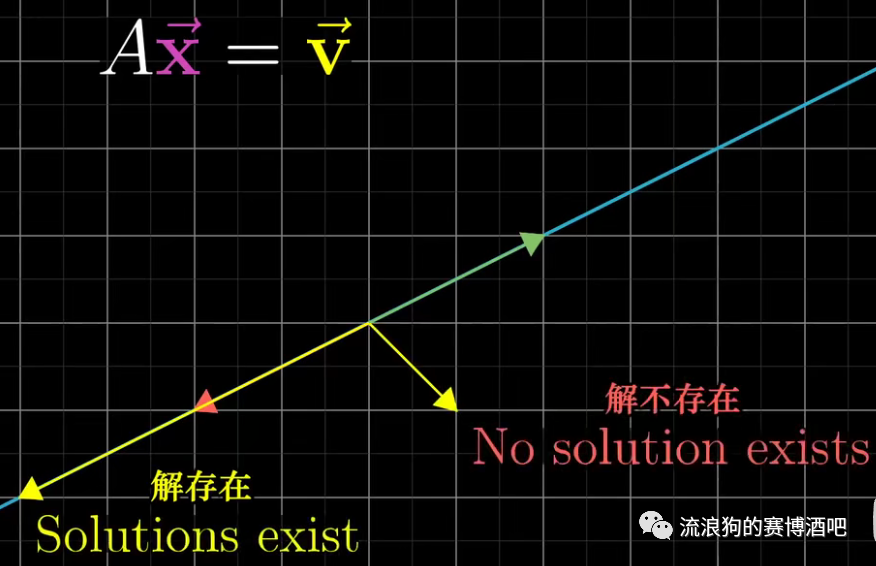
2.5 秩(rank)与列空间(column space)
2.5.1 秩与维度
如上章所说,有的线性变换会压缩空间的维度。例如三维空间压缩为平面,或直线。
如果一个变换使结果呈现为一条直线(1 dimensional),则我们称这个变换的秩为1。相应的,如果结果为平面,则秩为2.
所以秩其实代表了变换后的空间维度。
2.5.2 列空间(column space)
无论是直线、平面或者三维空间,一个矩阵所有可能的变换结果的集合,被称为矩阵的列空间。
因为一个矩阵的列(column)表示出了所有基向量在经历线性变换后的位置
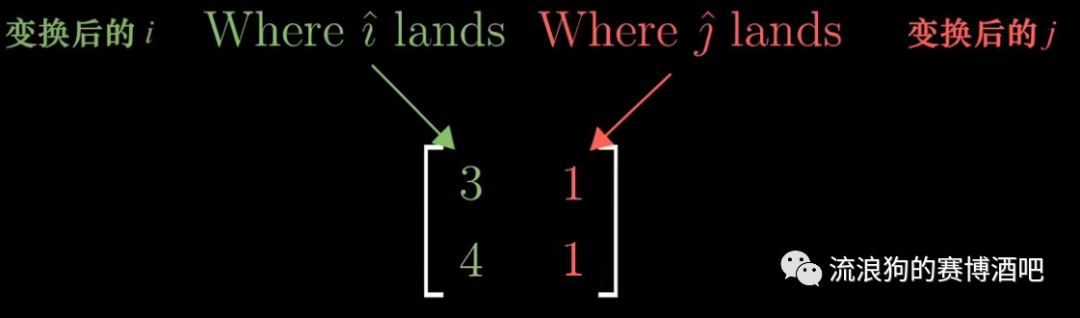
而列空间,就是这些变换后的基向量所能够张成的空间。

所以,列空间就是矩阵的列所张成的空间。更精确一点,秩其实对应的是列空间的维数。
2.5.3 满秩
当一个矩阵的秩达到了其所能达到的最大值时,意味着秩与列数相等,这种情况称为满秩(full rank)。
对于一个满秩的矩阵来说,在变换后唯一落在其原地的就只有原点。
2.5.4 核(kernel)/零空间(null space)
而对于非满秩矩阵来说,由于它把空间压缩至更低维度,这代表非常多的向量在变换后成为了零向量。
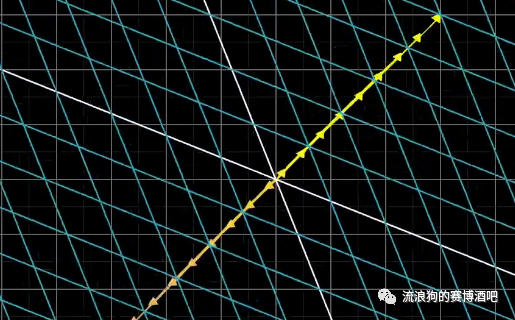
对于秩为1的2x2矩阵,有垂直于压缩后直线的一条直线,其上所有向量被压缩至原点。
对于秩为2的3x3矩阵,同样有垂直于压缩后形成的平面的一条直线,其上所有向量被压缩至原点。
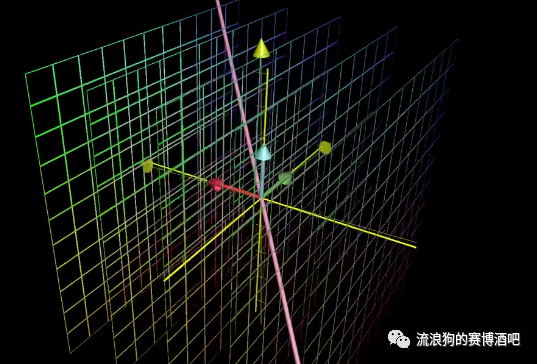
对于秩为1的3x3矩阵,有一整个垂直于压缩后形成的直线的平面,其上所有向量被压缩至原点。
这些变换后落在原点的向量的集合,被称为矩阵的kernel或者null space。而零空间,正是这些向量所构成的空间。
所以对于线性方程组来说, 当向量为零向量时,零空间就是这个矩阵所张成的所有空间。






