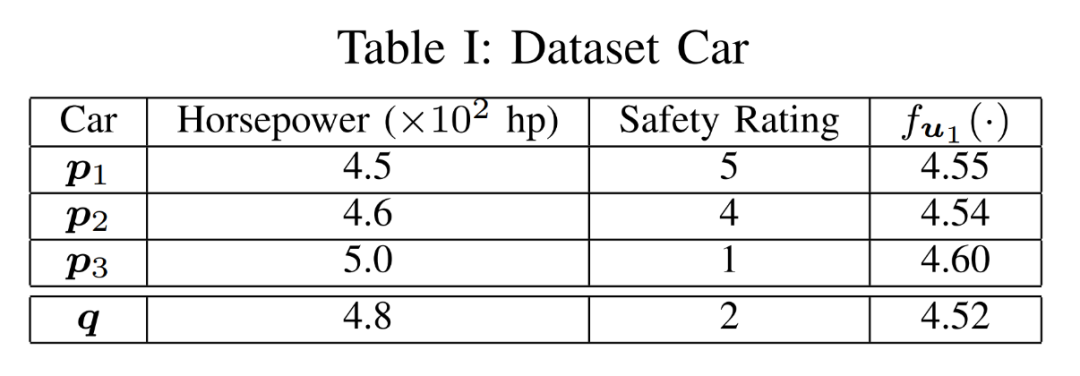
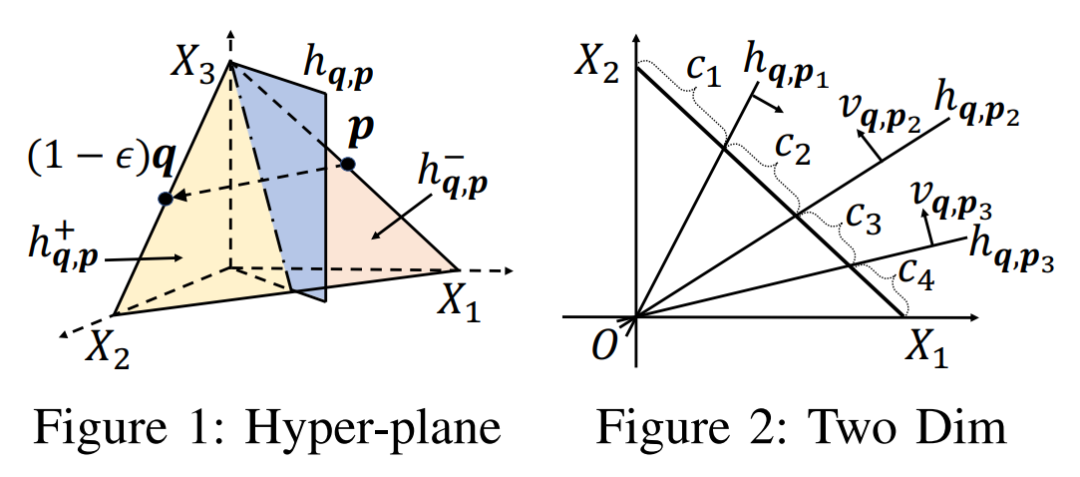
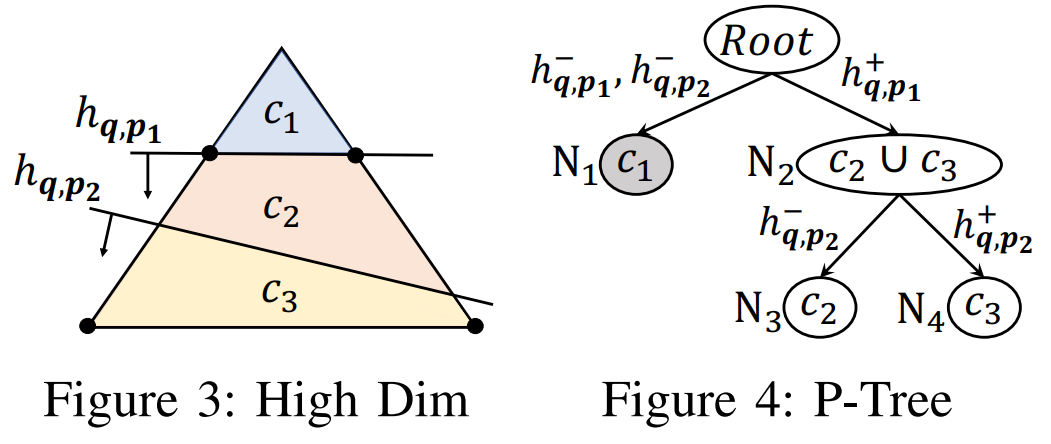
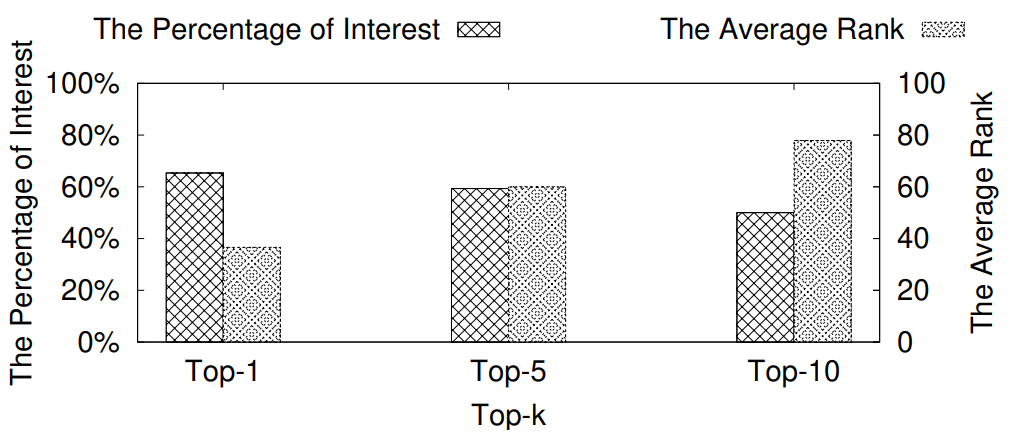
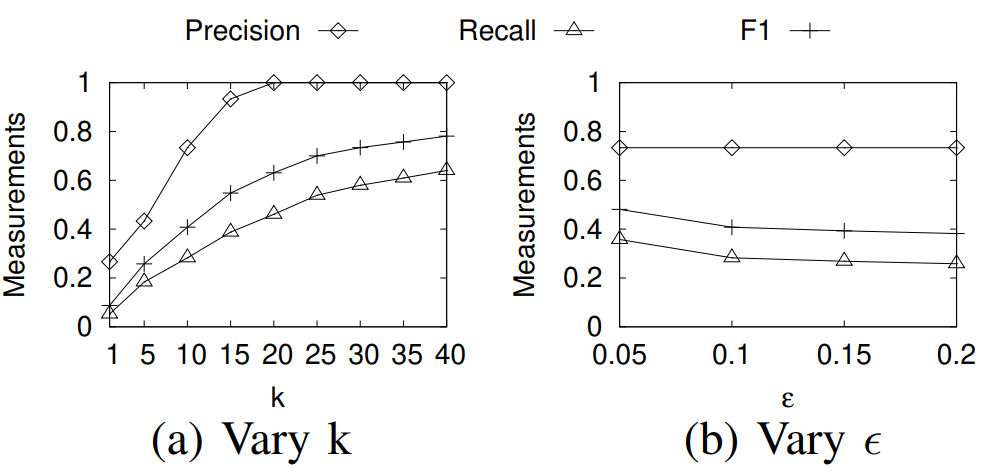
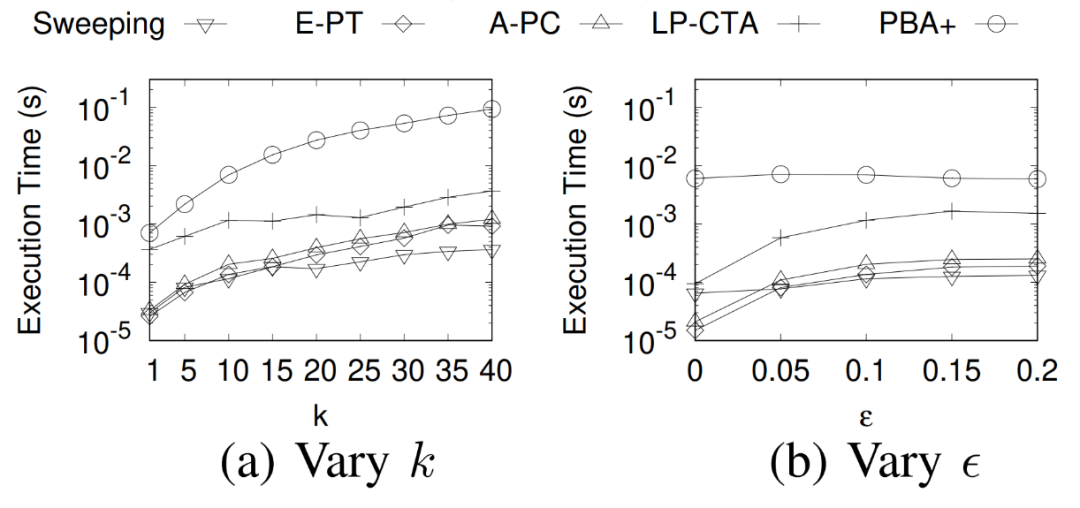
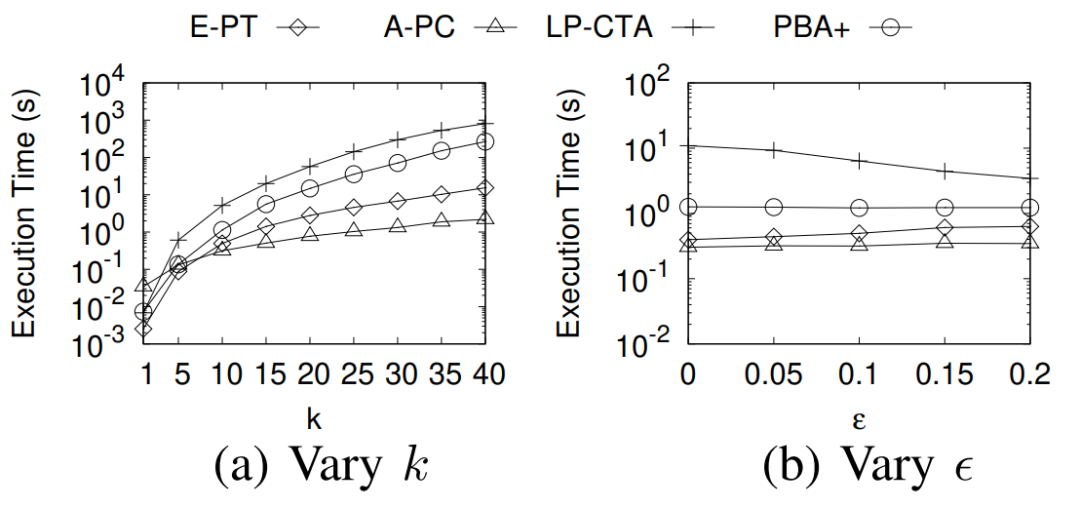
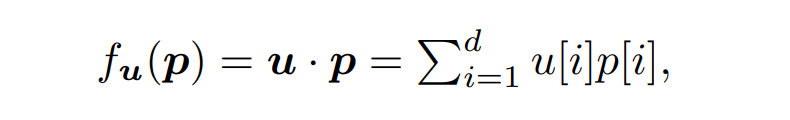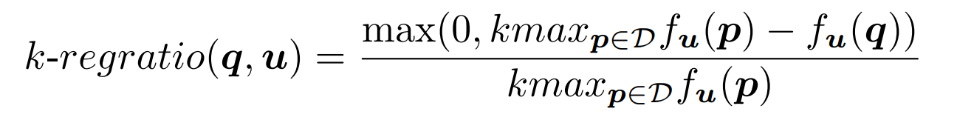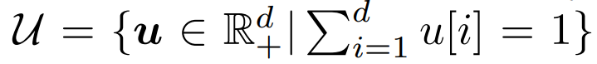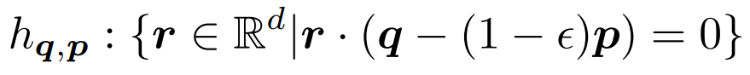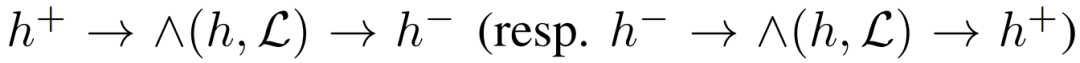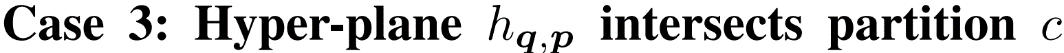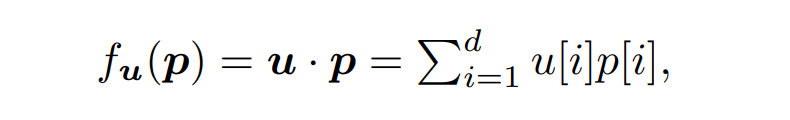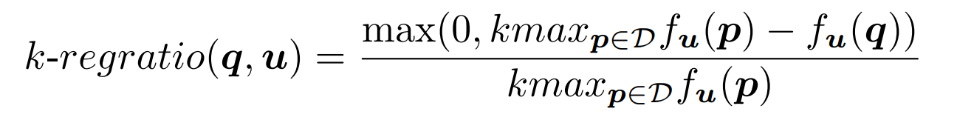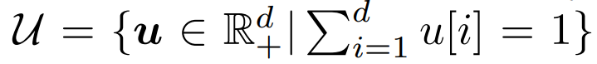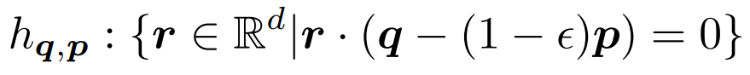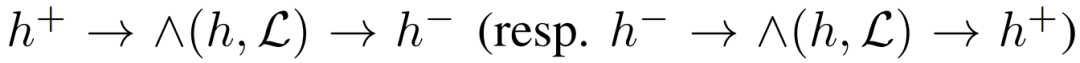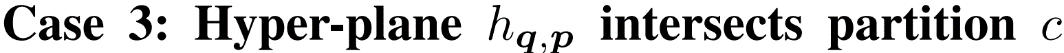互联网决策领域对反向查询的算法的需求越来越明显,运营商在获取用户对产品的偏好程度时常常也需要获取可能对某种产品最感兴趣的用户群体以实现个性化推荐。本次为大家带来数据库领域顶级会议ICDE 2024的文章《Reverse Regret Query》,本文在举办于荷兰乌德勒支的第40届ICDE会议上获得ICDE 2024 Best Paper奖项。当下,多准则决策问题的反向问题变得越来越重要,正向问题的目的是找出符合客户偏好的产品,而反向问题的目的是找出可能对特定产品感兴趣的潜在客户。例如对于一个汽车制造商来说,考虑一组产品以及两个属性,对每一个用户,使用效用函数fu表示用户对产品的偏好程度(每个用户的效用函数不同),如表1所示,用户有更高的可能购买效用函数更高的产品,对一个用户来说,如果某种产品的效用函数较大,则代表该用户是产品的潜在用户。反向查询的目的是给定一个产品,找到那些产品的潜在用户,即效用函数高的用户,当前的最具有代表性的算法是反向Top-k查询,它会根据产品的效用函数以递减的顺序排列产品,然后返回排序在Top-k位置内的用户和效用函数。Top-k算法有几个主要问题: 搜索具有局限性:反向Top-k查询着眼在产品排名上,而这是从产品评分中推导出的次要信息来源,该信息强调了产品的相对位置,而没有考虑到它们的得分差异,这可能会模糊产品对潜在客户的细节,例如当不同产品的属性较接近时效果往往不佳。度量不合理:反向Top-k查询简单地使用得分和排名来评估用户偏好,而没有与所有产品进行总体的结合计算。针对上述两个问题,论文提出反向遗憾查询问题(RRQ)及其解决方法,使用遗憾率这一度量代替简单的评分进行评估。原本的遗憾率的概念是以最高分为支点的,然而这种度量有时可能过于严格,为了适应各种情况,论文将比较基准从最高分放宽到第k个最高分,其中k ≥ 1。具体来说,论文做出以下贡献:(1)首次提出RRQ问题,该问题采用改进的遗憾率度量,通过对产品的全面评估来有效识别潜在客户。(2)针对RRQ的二维特殊情况提出了Sweeping算法,其中每个产品都由两个属性描述,Sweeping算法仅需要线性时间成本;针对RRQ的一般情况提出了两种算法,其中每个产品都由多个属性描述。算法E-PT是一种返回完整结果(即所有潜在客户)的精确算法,算法A-PC是其速度更快,忽略部分准确度的近似算法。对合成数据集和真实数据集的实验表明论文使用的遗憾率可以合理而有见地评估潜在客户,提出的RRQ求解算法比现有算法快几个数量级。点:输入由n个产品和一个查询产品组成的集合D,每个产品由d个属性描述,则可以将每个产品表示为一个d维点p = (p[1], p[2], ..., p[d]),每个维度都归一化为 (0, 1],且用户更喜欢维度上的更大值。该函数广泛用于建模顾客偏好,已进行的实验研究表明,线性效用函数可以有效地捕捉顾客对产品的评价。每个效用函数对应一个效用向量u = (u[1], u[2], ..., u[d]),该向量表示每个属性对顾客的重要性。u[i] 越大表示第i个属性对顾客越重要。所有效用向量的定义域U称为效用空间。此外,函数得分 fu(p) 也称为p相对于u的效用,表示用户对点p的偏好程度。如果顾客更喜欢p而不是q,则 fu(p) > fu(q)。遗憾点:给定一个效用函数fu,数据集D中的点可以根据它们相对于u的效用按降序排列。用kmaxp∈D fu (p)表示第k个点的效用。例如,在表II中,由于点p1排名第二,有2maxp∈D fu (p1) =fu (p1) = 0.56。为了评估查询点q,给定数据集D和效用函数fu,定义查询点q的k-遗憾率为:k-遗憾率的值能够衡量q与D中相对于u的第k个点的效用有多接近,显然k-遗憾率保持非负,在范围[0,1]内。如果k-遗憾率低于一个阈值ϵ(k-regratio(q,u) < ϵ),则q的效用仅比第k个点的效用略小甚至更大。在这种情况下,产品更加受到用户的偏好,用户更加不容易感到“遗憾”,则称点q是相对于 u的 (k , ϵ) 遗憾点。给定一个数据集D、一个查询点q、一个整数k和一个阈值ϵ,RRQ问题的目的是找到所有u∈U,使得q是相对于u的 (k , ϵ) 遗憾点。RRQ问题中有两个参数k和ϵ。参数k控制枢轴点的选择,如果k较小,问题将重点关注最佳点作为枢轴。参数ϵ决定查询点和所选枢轴之间所需的接近程度,较小的ϵ意味着将点视为足够接近的标准更严格。效用空间U是一个包含无限效用向量的连续空间,问题的完整输出是U中包含合格效用向量的区域,此类区域称为合格区域。 论文从几何角度形式化RRQ问题,在d维几何空间Rd中,每个效用向量u ∈U都可以看作一个点。对于每个维度,u[i] ≥ 0,并且和为 1。效用空间 为:例如,当d = 2时为线段(如图2所示),或当d = 3时为三角形(如图1所示)。对于任何点p∈D,可以在几何空间Rd中构建一个超平面hq,p,其中包含查询点q:超平面通过原点,其单位向量与q− (1−ϵ) p的方向相同。图1展示了一个例子,对于每个效用向量u,有u · (q − (1 − ϵ)p) = 0,即 fu(q) = (1 − ϵ)fu(p)。超平面hq,p将效用空间分成两个半空间。hq,p上方的半空间hq,p+(黄色部分)称为正半空间,包含所有满足 fu(q) = (1 − ϵ)fu(p) 的效用向量u,与之相反,hq,p下方的半空间hq,p−(红色部分)称为负半空间。超平面hq,p的单位向量(黑色箭头)指向正半空间。接下来将超平面、半空间概念应用于RRQ,对于每个点p∈ D,构建一个关于q的超平面hq,p,将效用空间划分为两个半空间。由于|D| = n,因此共有n个超平面和2n个半空间。n个超平面将效用空间划分为O(nd-1)个区域,称为分区,每个分区由n个(正或负)半空间覆盖,此外,如果分区中的任何效用向量都在半空间中,也称分区被半空间覆盖。如图2所示,三个超平面将效用空间划分为四个分区c1、c2、c3和c4。分区c1由一个负半空间hq,p1−和两个正半空间hq,p2+,hq,p3+覆盖。以下引理说明如何确定查询点是否是相对于分区中的效用向量的(k , ϵ)遗憾点:当且仅当分区c被少于k个负半空间覆盖时,查询点q是相对于分区c中任何效用向量的(k , ϵ)遗憾点。基于引理,可以分以下三步解决RRQ问题:(1)为每个点构建一个超平面;(2)根据构建的超平面计算分区;(3)获得被少于 k 个负半空间覆盖的分区。以图2为例,假设k = 2,分区c1、c2、c3将被返回,因为它们被少于两个负半空间覆盖。在如图2所示的二维几何空间中,效用空间U是从(0,1)到(1,0)的线段L。一旦效用空间被超平面划分,分区就是L的有序子段(例如,在图2中有c1→c2→c3→c4)。Sweeping算法沿L(从(0,1)到(1,0))进行扫描并按顺序检查每个分区。如果分区被少于k个负半空间(即多于n − k个正半空间)覆盖,则它是一个合格的分区,可以返回。但是有两个问题会影响Sweeping的效率。首先,由于每个p ∈D都会创建一个超平面,需要检查的分区数量较多;其次,检查分区是否符合返回条件的成本很高。接下来对算法在这两个方面的优化进行讨论。令r = (1, 0)在L中是空间R2中的参考效用向量。如果超平面的负半空间包含r,则称该超平面为包含超平面,否则称其为排他超平面。在图2中,hq,p2和hq,p3是两个包含超平面,hq,p1是排他超平面。对于所有包含超平面,根据它们与L的交点对它们进行排序。用∧(h , L)表示超平面h与L的交点。如果∧(h , L)距离X1轴较远,则超平面h的排名较高。例如在图2中,超平面hq,p2的排名高于超平面hq,p3。稍微滥用符号,将排名为k的包含超平面表示为lhk。可得引理:查询点q不是相对于lhk 的负半空间中任何效用向量的(k , ϵ)遗憾点,根据该引理可得lhk-中的分区不符合返回条件,可以直接省略这些分区。例如图2,其中k = 1。由于包含超平面hq,p2排名第一,因此可以省略分区c3 ⊆ hq,p2−和c4 ⊆ hq,p2−。类似地,可以根据所有排他超平面与L的交点对其进行排序。交点离X2轴越远,超平面的排名就越高。将排名第k的排他超平面表示为uhk,则uhk−中的分区也可以省略,基于该分区减少策略,能够减少需要考虑的分区数。回想之前的章节,算法的扫描方向是从(0,1)到(1,0),对于每个包含 (或排除) 超平面 h,扫描路径为: 因此当扫描到达包含 (或排除) 超平面h的∧(h , L)时,剩余要扫描的部分被h−覆盖 (或未被h−覆盖)。例如图2中的包含超平面hq,p2,扫描到达交点∧(hq,p2, L)时,将要扫描的部分,比如c3和c4,必须被hq,p2−覆盖。按照这个想法,论文维护一个整数Q来跟踪扫描期间负半空间的数量。假设当前正在扫描分区c,Q保存覆盖c的负半空间数量。随着扫描的推进,扫描到达交点∧(h , L),下一个分区为c′,如果超平面h是包含超平面,则其负半空间必须覆盖要扫描的剩余分区(包括c′),接下来就可以更新Q并简单地获得覆盖c′的负半空间数,总的流程为:首先找到超平面lhk和uhk,并排除负半空间lhk−或uhk−中的分区,然后从∧(uhk , L)的下一个分区开始扫描过程,并将Q设置为覆盖它的负半空间的数量。扫描向∧(lhk , L) 移动。当到达包含(或排除)超平面h的交点∧(h , L)并进入新的分区c时,Q会通过加(或减)1进行更新,接下来检查分区c是否符合返回条件。当uhk+∩lhk+中的所有分区都被扫描后,算法过程停止。例如图2中k = 1的情况,有三个超平面hq,p1、hq,p2和hq,p3,其中uhk=hq,p1,lhk=hq,p2,接下来排除分区c1、c3、c4,因为它们位于hq,p2−或hq,p2−中。扫描从∧(hq,p1, L)开始到∧(hq,p2, L),对于分区c2,Q = 0 < k,因此它作为最终输出返回,即C = {c2}。 论文的多维搜索算法涉及一些复杂的几何原理,受篇幅限制优化和近似部分(A-PT)不详述,具体了解请查阅原文。简单来说,论文构建了一个树形结构索引,称为分区树(简称P树,如图4),用于管理效用空间中由超平面划分的分区。对于每个点p∈ D,使用查询点q构建超平面 后将其插入到P树中。P树会逐步索引迄今为止插入的超平面划分的分区,进行动态更新。插入所有超平面后返回P树中被少于k个负半空间覆盖的分区。在P树中,每个叶节点包含一个分区,每个内部节点包含其可到达叶子节点的分区的并集,与二维算法类似,使用计数器Q来记录覆盖存储在节点N中的分区的负半空间的数量。以图3为例。效用空间被两个超平面hq,p1和hq,p2分成三个分区,图4显示了相应的P树。分区c2∪c3既不被hq,p1−也不被hq,p2−覆盖,因此Q(N2) = 0。P树通过每次插入一个超平面来逐步的,首先构建根节点,其分区是整个效用空间。插入超平面时,存储在某些叶子节点中的分区会被划分为更小的分区,从而导致这些叶子节点分裂。插入一个节点时有以下几种情况:此时保持分区不变,把Q (N)加1,若Q (N) ≥ k,则节点已经无效,不再进行处理,如果Q (N) < k且N为内部节点,则递归处理N的所有子节点。此时如果节点N是内部节点,则插入过程直接跳转到其子节点。否则,为N构建两个子节点N′和N′′,分别包含c的两个子分区。确切地说,第一个子节点包含分区c ′ = c ∩ hq,p−, Q(N′) = Q(N) + 1;第二个子节点包含分区c′′ = c ∩ hq,p+ , Q(N′′) = Q(N)。对于节点N′ ,如果Q(N′) ≥ k,则直接标记为无效。处理所有节点后, P树中被少于k个负半空间覆盖的分区即为结果。实验设备:CPU为3.10GHz、RAM为16 GB的计算机数据集:合成数据集(反相关、相关、独立)代表多准则决策中的典型数据分布。真实数据集是四个真实采集的数据集,例如数据集Island包含63,383个二维地理位置,所有数据集均经过了归一化处理。实验参数:通过改变以下参数来评估算法:(1)参数 k;(2)阈值 ϵ;(3)维数 d;(4)数据集大小 n;(5)数据集类型评估基准:根据执行时间对论文算法与现有方法LP-CTA和PBA+进行了评估,为每个维度分配(0, 1]范围内的随机值来生成30个查询点,然后使用这些查询点测试每个算法,运行30次,并报告平均结果。论文探索了反向Top-k查询和论文提出的反向遗憾查询之间的差异。首先对Car数据集进行了用户研究,以比较产品排名和产品效用以评估产品。作者招募了 30 名参与者,并使用交互式算法Adaptive来学习他们的确切效用函数,向每位参与者提供他们的前k辆汽车(即效用最高的k辆汽车),声称这些结果会引起他们的兴趣,其中k有三种设置:k = 1、k = 5 和 k = 10,然后找到k-遗憾率小于0.1的汽车,并均匀地选择其中的五辆,要求参与者表明他们是否对这五辆选定的汽车感兴趣。作者收集两类结果:(1)兴趣百分比,即在五辆选定的汽车中,参与者感兴趣的汽车的百分比;(2)平均排名,即在五辆汽车中,参与者感兴趣的汽车的平均排名。图6展示了结果:结果表明,作为从产品效用中得出的次要信息来源,排名不足以确定顾客的兴趣,直接关注效用的遗憾率在建模顾客对产品的偏好方面效果更好。其次,作者将反向遗憾查询的结果与反向Top-k查询的结果进行了比较。用S表示在用户研究中学习到的效用函数集。对于不同的k和ϵ,确定子集S1 ⊆S 和S2 ⊆S,它们分别包含反向Top-k查询和反向遗憾查询结果中的效用向量。为了进行比较,将S2视为假设的基本事实(而非真正的基本事实),获得S1的准确率、召回率和F1。图7显示了结果,表明反向遗憾查询在寻找潜在客户方面更有效:合成数据集的二维问题中,Sweeping的速度分别是现有算法LP-CTA的20倍和PBA+的60倍。此外,ε增加时, Sweeping的执行时间几乎没有变化, 这验证了Sweeping在不同参数设置下的稳定性:真实数据集上,E-PT和A-PC在执行时间上远远优于竞争对手。例如当k = 40时,E-PT和A-PC在NBA数据集上最多花费15.4秒,而现有算法LP-CTA和PBA+ 分别花费810.1秒和266.2秒。在不同类型的数据集、维度数量和数据量下算法都具有较大优势,这证明了算法的可扩展性和稳定性。 论文创新地提出RRQ问题,用户研究证明与现有的反向Top-k查询相比,RRQ能够更好地评估潜在客户。RRQ旨在通过查找所有效用向量来确定给定产品的潜在客户,使得给定产品是(k, ϵ)-遗憾产品,首先对于二维情况,即每种产品都由两个属性描述,论文提出了仅需线性时间的Sweeping算法;其次考虑一般情况,即每种产品都可以用多个属性描述,论文提出了一种精确算法E-PT 和一种近似算法A-PC,它们在理论和经验上都表现良好。| 重庆大学计算机科学与技术(卓越)2022级本科生,重庆大学Start Lab团队成员。 | |
重庆大学时空实验室(Spatio-Temporal Art Lab,简称Start Lab),旨在发挥企业和高校的优势,深入探索时空数据收集、存储、管理、挖掘、可视化相关技术,并积极推进学术成果在产业界的落地!年度有3~5名研究生名额,欢迎计算机、GIS等相关专业的学生报考!
图文|高研盛
编辑|李佳俊
审核|李瑞远
审核|杨广超