海量科学数据正面临着存储与管理难题,这使得有损压缩算法得到了广泛关注。现有的有损压缩算法主要是以误差控制为驱动的,例如事先规定误差边界再进行压缩;然而,由于存储、网络资源等限制,需要在有限的空间(目标压缩率)下尽可能降低数据的失真情况,而前者无法直接适用于这类需求。本次为大家带来数据库领域顶级会议ICDE 2023的论文:《A Feature-Driven Fixed-Ratio Lossy Compression Framework for Real-World Scientific Datasets》,论文提出了一种可固定压缩率的有损压缩框架,具有低计算开销、压缩器无关、数据特征驱动等特点。
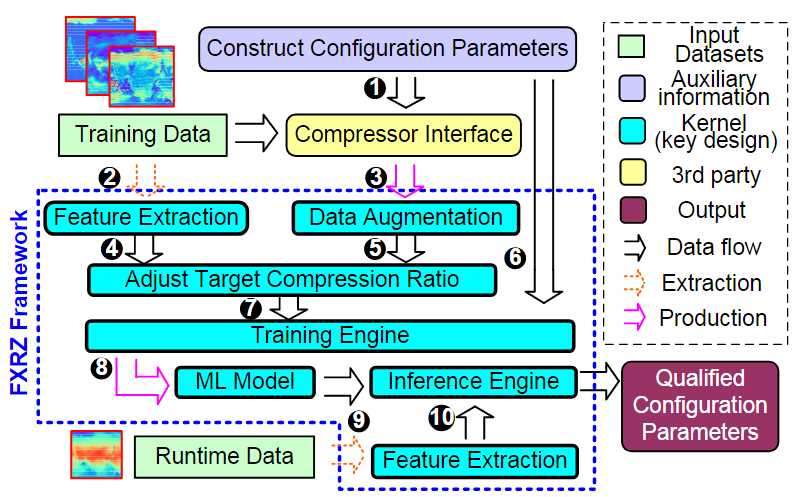
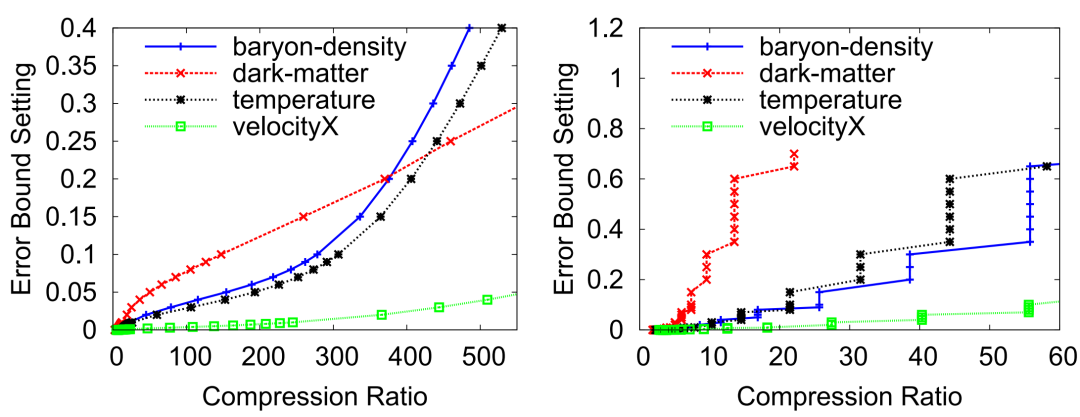
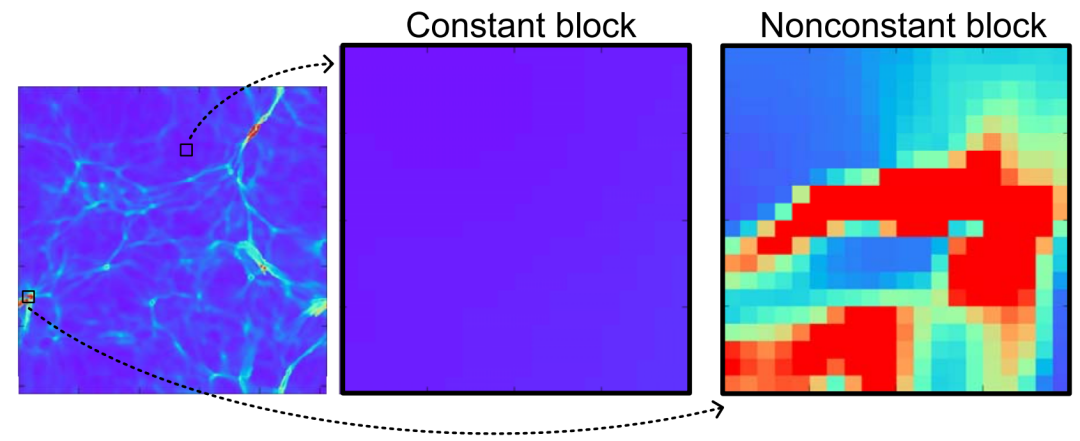
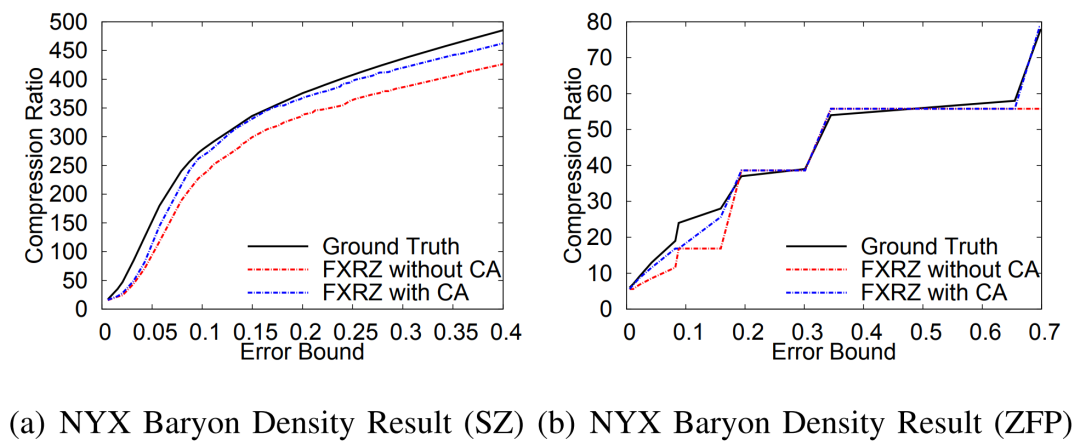
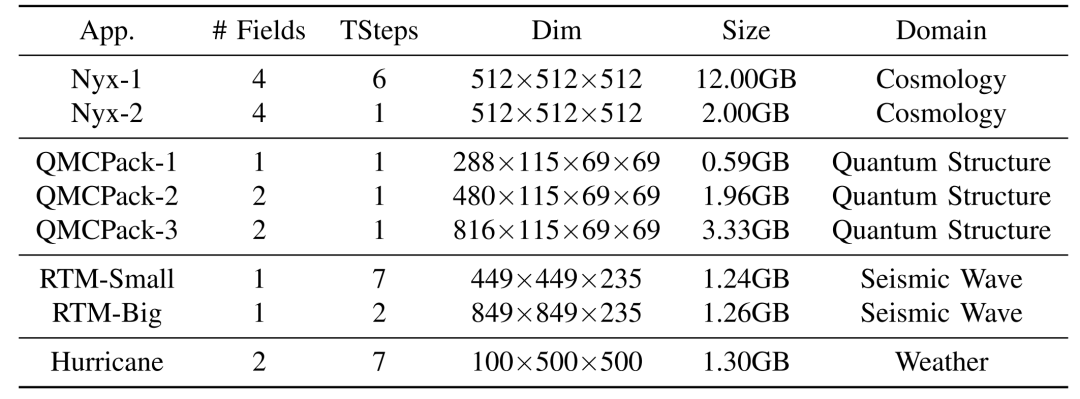
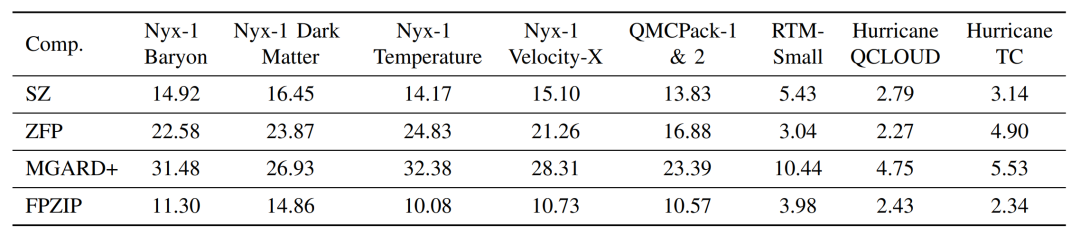
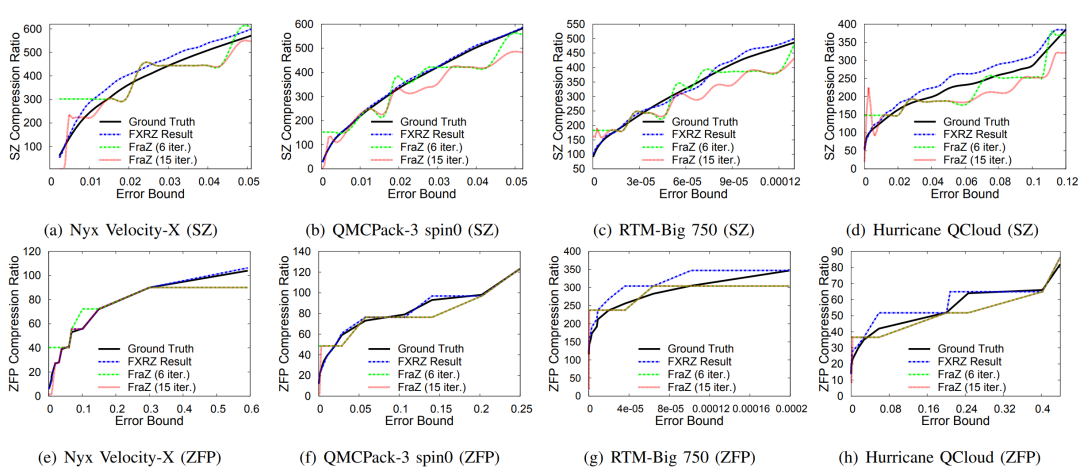
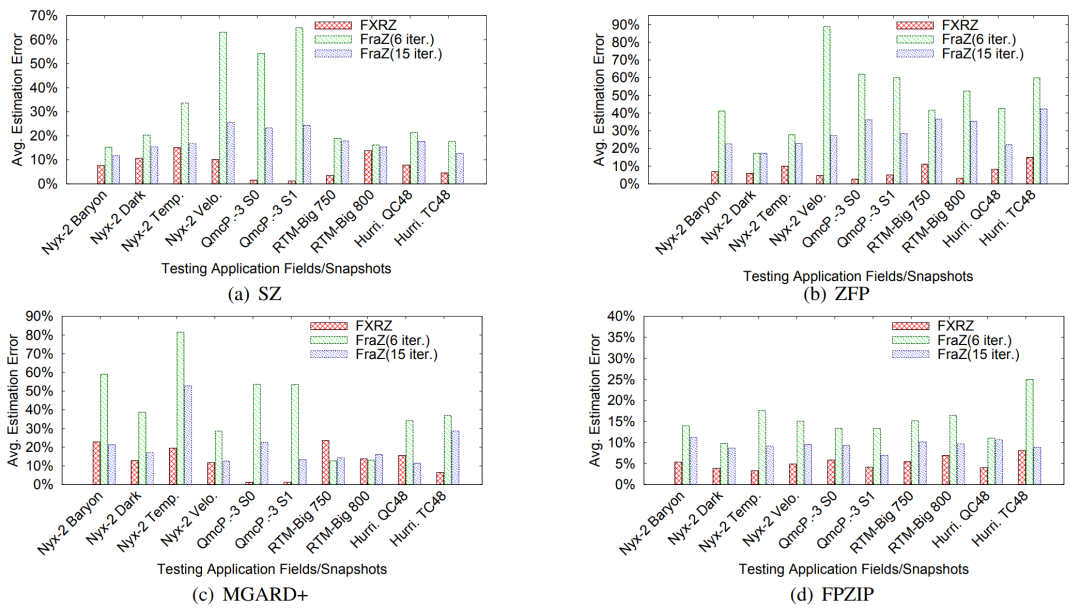
当前科学应用或仪器在模拟或进行数据采集的过程中往往会产生海量的数据,诸如Nyx这样的宇宙学模拟应用每次运行可产生数百PB的数据。因此,如何大幅压缩这些数据以更好地利用可用计算资源是当今科学数据管理的一个研究重点。利用数据压缩技术解决科学大数据问题已经取得了重大进展。一方面,目前已有多个库/工具包(如H5Z filter、pNetCDF-SZ)实现了面向科学数据库/格式(HDF5, ADIOS2)为用户提供透明的无损/有损压缩处理。另一方面,近年来针对科学数据集也开发了一些误差有界的有损数据压缩算法(如SZ、ZFP、FPZIP、MGARD等),根据用户指定的误差边界尽可能地提高压缩率。 然而,为了优化数据管理、存储或传输性能,开发一种有效的“固定比率压缩机制”在实践中也是至关重要的。具体来说,系统需要在控制数据大小的情况下执行数据压缩,其适用场景主要是基于受限的数据传输带宽/存储空间/内存空间尽可能地保持最佳数据质量。现有的误差有界有损压缩算法根据绝对误差界、相对误差界和峰值信噪比(PSNR)等多种类型的误差指标进行压缩,但遗憾的是不能够根据用户需要的目标压缩率来压缩数据。为此,FRaZ进行了对构建通用的固定压缩率有损压缩框架的首次尝试,但其基于试错的迭代搜索方法计算开销过大,往往与压缩时间在同一数量级或者更甚,难以适用于数据的在线压缩处理。为了解决上述问题,论文尝试分析了数据特征与压缩率之间存在的联系,并进而提出了一种高效的、与压缩器无关的特征驱动的固定压缩率有损压缩框架FXRZ。它可在运行时有效地提取并分析数据特征,并借此根据用户指定的目标压缩率提供最合适的误差边界配置。给定一个多维科学数据集D,一个误差控制的有损压缩器C (SZ, ZFP, FPZIP 或 MGARD+) 和一个目标压缩率(表示为TCR),FXRZ从数据集D中提取关键数据特征并估计误差边界设置(表示为Ep),使得在Ep下实际测量的压缩率(表示为MCR)足够接近目标压缩率(表示为TCR)。最后,将MCR与TCR进行比较以验证FXRZ的准确性。因此,对于给定的D、C和TCR,本论文的研究目标是以较低的性能开销最小化MCR和TCR之间的差异,即min(|MCR-TCR|)。 FXRZ的基本设计思想是从训练数据集中探索关键的数据特征,并使用有效的数据增强技术快速生成充足的压缩结果(其中只有极少部分需要进行压缩)进行ML模型训练,然后在运行时利用该模型来预测目标压缩率所需的最佳误差配置。其整体设计框架如下图所示:1)特征提取模块:特征提取模块用于提取数据的分布特征,用于在训练阶段②构建ML模型,并在推理阶段⑨作为输入参数预测最佳的合格误差界设置。2)数据增强模块:数据增强模块是对运行不同有损压缩器①和③所产生的压缩结果进行增强。3)模型训练模块:训练模块是FXRZ的核心模块,它根据提取的特征向量④、增强的压缩结果⑤和相应的配置参数⑥三部分信息进行ML模型的训练工作,并基于动态目标压缩率调整策略⑦优化误差界估计。 4)推理引擎模块:生成训练良好的ML模型⑧后,借助推理引擎模块,即可根据运行时提取的特征向量⑩,预测最合格的误差边界设置,从而达到目标压缩率。由于ML模型训练阶段需要掌握尽可能多的在不同数据集和不同误差界设置下的压缩率情况,这将不可避免地导致执行大量的压缩操作。因此,通过运行有损压缩算法生成大量压缩结果样本的代价是非常高昂的。对此,论文提出使用基于插值的数据增强方法以减少所需的压缩操作。以图2为例,论文发现有损压缩器在相近的误差界下的压缩率是非常接近的。虽然误差界与压缩率之间不是线性关系,但两个连续的驻点之间的关系近似为线性关系。因此,可以利用线性插值(或最小二乘法)来增加压缩结果样本。具体地说,可以先运行指定的压缩器进行几个有代表性的误差边界设置,以生成一定数量的真实压缩率。将这些结果视为驻点,进而利用线性插值方法得到其他压缩率下的结果。这种增广的压缩结果曲线构成了以压缩率为自变量的误差界设置函数,从而可以在训练阶段为任意给定的压缩率获取一个期望的误差界。论文观察了不同数据特征对有损压缩器效果的相关系数,如表1所示。进而为FXRZ框架选取了Value Range, Mean Value, MND, MLD, MSD五种数据特征,分别为:1)Value Range:数据集的值范围,表示数据集中数据偏离的程度(或数据集的幅度)。2)Mean Value:数据集中所有数据点的平均值。3)Mean Neighbor Difference(MND):平均邻居差值,表示所有数据点与其各邻居的平均绝对差值的平均值。4)Mean Lorenzo Difference(MLD):平均洛伦兹差值,表示数据值与其洛伦兹预测值之间的平均绝对差值。公式(1)(2)分别展示了如何对二维和三维数据集中的数据进行洛伦兹预测。5)Mean Spline Difference(MSD):平均样条差值,指数据集中所有数据点的特定三次样条插值拟合误差的平均值。公式(3)展示了如何对一维数据集中的点计算三次样条插值拟。类似地,对于多维数据集,可利用式(3)分别沿各维计算splinei,并计算其平均值A。最后,考虑当前数据值与A之间的差值作为当前数据点的MSD值。 对于任何数据集,FXRZ使用5个提取的特征和1个目标压缩率作为ML模型的输入。在推理阶段,模型需要能够预测期望的误差界设置。由于误差界的预测值可能是任何浮点数,故而首先排除了分类器模型。进而论文选择了三个流行的ML模型:Support Vector Regressor (SVR),AdaBoost Regressor,Random Forest Regressor (RFR)并尝试应用于FXRZ框架。对于这些模型,论文使用k折交叉验证来调整超参数并提高性能,测得各模型的平均预测误差如下表所示:结果显示SVR、AdaBoost并不适合FXRZ框架。论文指出SVT效果不佳的关键原因是最佳拟合误差配置有时不能充分分离,因此不足以构建超平面来区分不同的压缩率结果;而AdaBoost在目标压缩率(及其相应的预期误差配置)相对较低时,误差边界设置的微小变化可能无法被AdaBoost回归很好地捕获,因此存在较高的估计误差。相较而言,随机森林回归器(RFR)表现最佳,论文分析这得益于其通过构建大量树来纠正过拟合问题的特殊能力。进而,论文选择为FXRZ框架采用RFR模型。为节约对数据集进行特征提取的时间,论文采用了均匀采样的策略。对于每个数据集,平均采样为样本容量的1.5%。论文分析了基于全采样和1.5%均匀采样时各自的平均压缩率预测误差,分别为8.24%和6.23%,准确率损失较少,但可使得特征提取的耗时缩减为原来的1/50。 论文指出,对于数据集中较为平滑的区域,压缩算法通常能够以极高的压缩率进行压缩处理,而这会使得FXRZ框架预测的压缩效果偏低。为此,论文引入了一种新的优化策略——压缩率调整(Compressibility Adjustment, CA),其根据数据密度对预设目标压缩率进行调整,从而提高FXRZ预测误差配置的准确性。具体来说,论文提出将数据集分成许多小块。如果某块内的数值偏差很小(小于均值的15%),则称其为恒定块;否则,称其为非恒定块。图4展示了示例数据集(Nyx Temperature,大小为512×512×512)中的恒定块和非恒定块:进而,论文提出数据集的可压缩性应仅由非恒定块决定,并给出相应的调整方法:其中,TCR为用户指定的目标压缩率,ACR为调整后的压缩率,R为给定数据集中非恒定块的百分比。接着,FXRZ使用ACR替换TCR作为目标压缩率输入至ML模型,并成功验证了CA这一改进策略的有效性,对比效果如下图所示: 作者在ANL Bebop的Intel Broadwell节点(Intel Xeon E5-2695v4)上进行实验,ANL Bebop是由Argonne实验室计算研究中心(LCRC)管理的超级计算机。Bebop的每个Intel Broadwell节点拥有128GB的DDR4内存和36个计算核心。其存储系统使用配备2个I/O节点的通用并行文件系统(GPFS),I/O带宽为2GB/s。论文选用来自不同领域的多个热门真实科学数据集进行实验,其中大多数可以从SDRBench数据库中下载,详见下表:论文选用了四种最先进的误差有界有损压缩算法以评估FXRZ框架,包括SZ,ZFP,FPZIP和MGARD+:1)SZ: 一种误差有界的有损压缩器,已在社区中得到了广泛的测试和使用。2)ZFP: 另一个误差有界的有损压缩器,它在科学数据集的有损压缩方面也非常有效。实验中使用的是最新发布的0.5.5版本。3)FPZIP: 一款出色的有损压缩器,支持通过设置一个精度参数(从1到32的整数)来对应不同的有效尾数位,从而控制数据的失真程度。4)MGARD+: 误差有界的有损压缩算法MGARD的加速版本。论文选取了此前唯一的与压缩器无关的固定压缩率有损压缩框架——FRaZ作为对照基准,并对其进行了相对公平的设置。论文强调了FRaZ的运行成本非常高,因为其需要迭代地搜索合适的误差边界设置,并按照每个试探的误差边界设置运行压缩算法,以判断压缩比是否能够满足要求。表4展示了FXRZ在不同应用数据集和压缩算法上的训练时间。对于每个应用和压缩算法,总训练时间包括获得驻点,通过插值增加数据和训练RFR模型的时间。如上图所示,FXRZ的训练时间开销非常低,平均为13.59分钟。得益于其利用线性插值扩展训练集的策略,FXRZ不需要大量运行压缩算法以获得充足的训练数据。此外,作者还强调该训练时间是一次性成本,即一次训练后,在应用FXRZ估计目标压缩率的误差界设置的推理阶段不需要再运行压缩算法。 图6 FXRZ与FRaZ(基于6次、15次迭代)的预测误差对比上图展示了FXRZ与FRaZ在不同数据集和压缩算法下的预测误差对比示例,实验结果表明FXRZ在大多数情况下表现出较高的精度,且避免了FRaZ多次迭代带来的巨大性能开销。此外,在图7中,论文对比了两个框架在4种有损压缩算法预测下,针对4个真实科学应用数据集的TCR(目标压缩率)和MCR(实际测量压缩率)之间的平均预测误差(以百分比表示): 图7 FXRZ和FRaZ(基于6次、15次迭代)在不同目标压缩比下的平均估计误差从中可以看出,在大多数情况下FXRZ的平均估计误差较低,预测准确性较高。具体来说,FXRZ框架在所有四个压缩算法下仅有8.24%的平均预测误差;而基于6次和15次迭代的FRaZ框架对四个压缩算法的平均预测误差分别为34.48%和19.37%。对于FXRZ,分析时间主要包括特征提取、计算非恒定块占比以及调用RFR模型进行预测的时间;对于FRaZ,分析时间是基于给定TCR迭代预测误差配置的搜索时间。 表5 FXRZ(15次迭代)与FRaZ的平均分析时间(相对于压缩时间)对比如上表所示,一方面FRaZ的分析时间成本明显大于FXRZ;另一方面,为了找到所需的配置,FRaZ可能比FXRZ平均慢108倍。在本文中,提出了一种可固定压缩率的有损压缩框架FXRZ,具有低计算开销、压缩器无关、数据特征驱动等特点,能够有效地根据目标压缩比预测适当的误差界设置,从而使实际压缩率更接近预设目标。在预测效果上,实验表明其平均预测误差仅为8.24%左右,即使训练数据来自不同的应用范围,FXRZ也仍然可以保持良好的准确性;在预测效率上,FXRZ的执行开销总是比基准FRaZ低得多(低一个或多个数量级),且平均在线分析时间只占压缩时间的14%左右,能够有效应对在线压缩需求。
徐小龙 重庆大学计算机科学与技术专业2020级本科生,重庆大学START团队成员。主要研究方向:时空数据压缩 | 
|
重庆大学时空实验室(Spatio-Temporal Art Lab,简称Start Lab),旨在发挥企业和高校的优势,深入探索时空数据收集、存储、管理、挖掘、可视化相关技术,并积极推进学术成果在产业界的落地!年度有2~3名研究生名额,欢迎计算机、GIS等相关专业的学生报考!