范围过滤器是一种查询范围成员关系查询的数据结构。范围查询在现代应用程序中十分常见,而范围过滤器通过排除空范围查询来提高查询的性能。然而,最先进的范围过滤器,如SuRF和Rosetta有着高假阳率或低吞吐量的问题。那应当如何解决这个问题呢?本次为大家带来顶级会议ICDE的论文:《REncoder:
A Space-Time Effcient Range Filterwith Local Encoder》

一.背景
范围查询是现代数据库应用程序中常见的操作。不像布隆过滤器只支持点查询,范围过滤器确定查询的范围是否包含任何数据项,它们可以通过消除空范围查询来减少I/O的数量。范围过滤器可以用在日志结构合并(LSM)树、B+树或者R树里面,节省磁盘I/O的消耗。
目前有四种最先进的范围过滤器:SuRF, Rosetta , SNARF 和Proteus。SuRF是基于trie的,它的关键思想是修剪trie的较低层,然后简洁地编码剩余的trie。但是SuRF并不能为假阳率(FPR)提供理论保证,且FPR在相关的工作负载中显著增加。而Rosetta通过使用布隆过滤器克服了SuRF的缺点,它将所有键的前缀组织成一棵线段树,并使用一系列布隆过滤器来存储线段树。然而由于对 Bloom 过滤器的大量查询,Rosetta 的内存性能相对较低。SNARF学习了密钥的CDF模型,然后使用该模型来存储数据信息并回答范围查询。通过使用学习到的模型,SNARF获得了较低的FPR。然而,与SuRF一样,SNARF的FPR在随着工作负载显著增加。Proteus结合了trie和布隆过滤器。它提出了上下文前缀FPR(CPFPR)模型,通过该模型,它可以选择一个设计(trie和布隆过滤器)来实现较低的FPR。然而,使用CPFPR模型需要在构建范围过滤器之前对工作负载进行采样,这对于某些用例来说是不切实际的。
设计一个高效的范围过滤器有三个主要目标。首先,范围过滤器必须紧凑,以便能够存储在内存中。其次,必须准确(即FPR低),以节省尽可能多的不必要的 I/O。最后,它必须很快,以免显着增加目标应用程序的 CPU 使用率。由于最先进的解决方案已接近空间的理论下限,因此论文重点关注提高范围过滤器的性能,同时保持空间效率。
论文提出了一种新的范围过滤器,称为REncoder。它将所有键的前缀组织到一个线段树中,并将线段树编码到一个布隆过滤器以加速查询。同时由于在实际应用中数据集/工作负载(键/查询)的多样性,论文还提出了优化的REncoder。它可以自适应地选择要存储的段树的多少,以在不同的数据集中保持效率。基于优化后的再编码器,论文提出了两个新版本:一个根据数据集选择开始级别(从哪个级别开始存储),称为REncoderSS;另一个根据工作负载选择结束级别(结束存储到哪个级别),称为REncoderSE。论文从理论上证明了REncoder的误差是有界的,并通过使用合成数据集和真实数据集进行了广泛的实验证明了REncoder的性能优于所有先进的范围过滤器。
二.方法介绍
2.1 REncoder介绍
以LSM树为例,为LSM树的每个SSTable构造一个REncoder。当执行一个点或范围查询时,在访问SSTable之前,首先会查询相应的REncoder,只有当REncoder返回true时才会从磁盘加载SSTable。每当LSM树执行合并操作时,都需要使用新项重新构建REncoder。下面先简单介绍REncoder的思想。
与Rosetta类似,REncoder将所有键的所有前缀组织成一棵线段树,使用线段树来支持范围查询,同时用布隆过滤器存储该线段树。线段树的每个节点对应一个范围,父节点的范围是其子节点范围的并集,同一级别的节点范围不重叠。线段树的节点记录其范围内是否存在某个键,这意味着对于每个键,线段树不仅记录该键本身的存在,还记录其所有前缀(包含该键的范围)的存在。图1显示了一个示例。将二进制键1101(13)插入线段树中,不仅会记录1101,还会记录110([12, 13])、11([12, 15]) 和1([8, 15])。这样就可以将范围查询划分为最多log2(R)个前缀的点查询,其中R是范围大小。例如,查询范围[0010,1111] ([2, 15]) 相当于查询前缀001([2, 3])、01([4, 7])、1 ([8, 15] 是否存在])。
REncoder的关键技术是使用布隆过滤器存储线段树,并使用一种紧凑的编码算法来提高速度。论文编码方法的关键思想是利用查询的局部性以减少内存访问的次数。论文将整个线段树划分为许多迷你树。然后将每个迷你树编码为一个位图:迷你树中的每个节点对应于位图中的一位。如果该节点存在,则将相应的位设置为1;否则,相应的位将被设置为0。所编码的位图称为位图树(BT)。编码后将每个BT独立插入布隆过滤器中,同一BT中的信息,即同一迷你树中的节点都被本地编码到布隆过滤器中。对于一个有N个节点的迷你树,其对应的BT的大小为N位。
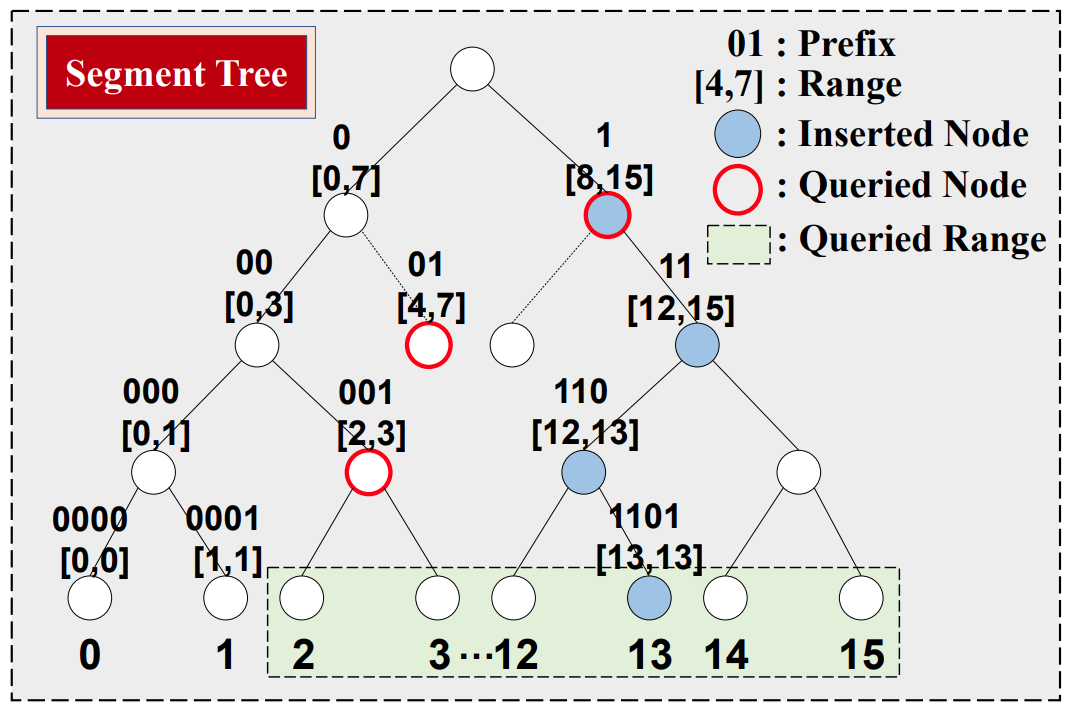
图1 线段树示例
2.2 构建REncoder
前文已经介绍了REncoder的基本情况,接下来介绍如何构建一个REncoder。
对于每个键,论文首先将它的所有前缀编码为若干个BT,然后将BT插入一个名为范围布隆过滤器 (RBF) 的特殊布隆过滤器中。RBF与标准布隆过滤器类似,插入位置由哈希函数计算。不同的是,标准Bloom过滤器一次只能插入一项,即一次将一位设置为1,而RBF将插入位置作为起点,并使用OR操作嵌入位图,从而同时将多个位设置为1。一旦所有键都被编码并插入到 RBF中,REncoder 的构建就完成了。
图2的左侧显示了一个REncoder的插入示例。插入分为三个步骤:
1)将键164(对应于10100100)分割为前缀1010和后缀0100。请注意,后缀 0100 实际上代表键164的最后4个连续前缀(10100、101001、1010010、10100100)。
2)将后缀0100编码为32位(4字节)的BT。首先,我们构建一个深度为5的虚拟线段树,它可以记录范围[0000,1111]。然后以广度优先的顺序对线段树的每个节点进行编号。根节点为第1个节点,0、01、010、0100分别对应第2、第5、第10、第20个节点。然后将BT中相应的位置设为1,得到BT 1100100001000000000100000000000,通过这种方式,论文将记录键0100的线段树编码为一个BT。
3)将前缀1010拼接到RBF的k个索引中,并使用操作OR镶嵌BT,这样就可以将所构建的虚拟线段树存储在RBF中。请注意,论文并没有构建一个真实的线段树,而是使用线段树的结构来组织键。下一个后缀1010的插入是相同的。请注意,在1010之前没有前缀。因此,哈希函数的前缀可以是0或任何其他常数。显然,在插入后,在RBF中设置为1的位数与Rosetta的布隆过滤器中的位数相同,这保证了REncoder的精度可以与Rosetta相匹配。
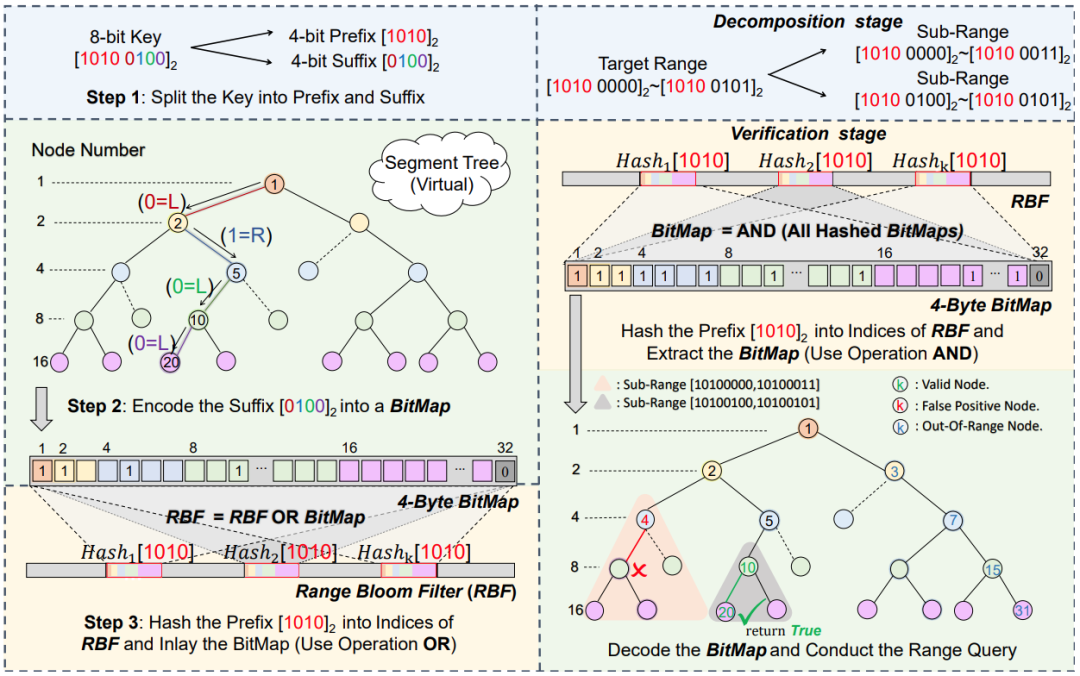
图2 REncoder的例子
2.3 REncoder的范围查询
REncoder和Rosetta在范围查询中的区别在于对布隆过滤器的查询。在Rosetta中,对布隆过滤器的每个查询可以检查是否存在一个前缀。在REncoder中,对RBF的每个查询都获得一个BT,该BT可以检查连续如干个前缀的存在性。由于范围查询的局部性,即在一个范围查询中经常访问连续的前缀,REncoder显著提高了查询效率。
接下来说明如何在REncoder中执行范围查询。查询过程分为分解阶段和验证阶段两个阶段。
1)在分解阶段,类似于Rosetta,论文将目标范围(Rt)分解若干个不重叠的子范围,每一个都对应于一个可以准确地覆盖范围内的所有键的前缀。论文将与当前前缀对应的范围表示为Rp。从最短的空的前缀开始,这意味着Rp是[0,maxkey],然后将Rp和Rt进行比较。有三种情况:(1)如果Rp和Rt不相交,那么就什么都不做;(2)如果Rp包含在Rt中,我们将Rp记录为一个子范围;3)如果Rp与Rt相交,我们将0(和1)附加到当前的前缀中以得到新的Rp[0,maxkey/2](和[maxkey/2+1,maxkey]),然后将新的Rp与Rt进行比较。重复上述过程,直到没有新的Rp为止。以4位键为例。对于目标范围[0,4],我们从最大Rp [0,15]开始。[0,15]与[0,4]相交,我们将[0,7]和[8,15]与[0,4]进行比较。[8,15]与[0,4]不相交,因此什么都不做。[0,7]与[0,4]相交,再将[0,3]和[4,7]与[0,4]进行比较。[0,3]包含在[0,4]中,我们将[0,3](对应于前缀 00)作为一个子范围。类似地,我们可以得到另一个子程序[4,4](对应于前缀0100)。
2)在目标范围分解后进入验证阶段。首先查询RBF是否存在与第一个子范围对应的前缀,如果它返回为负数,那么我们将继续查询与下一个子范围对应的前缀,直到查询完所有的前缀为止。如果它们都没有返回正值,则REncoder将报告目标范围为空。如果其中一个查询返回正,则对与该前缀对应的迷你树执行深度优先遍历,以进一步验证它的存在。遍历过程如下:从迷你树的根节点开始,查询RBF中是否存在与当前节点对应的前缀,如果返回为正值,则继续向下遍历树,否则终止当前路径。如果遍历到达一个叶节点,并且对RBF的查询返回正数,则REncoder报告该子范围不是空的,这也表明目标范围不是空的。否则,REncoder将报告该子范围为空。请注意,只有当验证阶段中的所有子范围都为空时,REncoder才会报告目标范围为空。
图2的右侧部分显示了一个REncoder的一个范围查询示例。假设目标范围为[160,165](对应于[10100000,10100101]),已插入键 164 和其他一些键(不包括在目标范围内)。首先将目标范围分解为两个子范围 [10100000, 10100011] 和 [10100100, 10100101]。然后进入验证阶段。对于子范围[10100000, 10100011](对应前缀101000),提取哈希前缀1010,通过它可以从RBF中获得BT 11111010010000100001000000000010。正如插入示例中所讨论的,BT 中的每个位对应于线段树中的一个节点。因此,可以将BT解码为线段树。然后发现BT中线段树的第4个节点(前缀101000)对应的位为1,所以开始遍历第4个节点对应的迷你树:首先检查前缀1010000,即遍历到8节点。由于前缀1010000的哈希前缀仍然是1010,所以不需要再次查询RBF,可以直接使用之前查询得到的BT(线段树)。结果发现BT中第8个节点对应的位为0,所以当前路径终止;然后检查前缀1010001,即遍历到9个节点。由于哈希前缀相同,因此仍然可以使用上一次查询得到的 BT,并且第9个节点对应的位也为 0。表明当前子范围为空,第四个结点恰好被其他BT设置为1。因此转而验证下一个子范围[10100100, 10100101](对应前缀1010010)。由于该子范围的哈希前缀没有改变,所以之前获得的BT仍然可用。首先查询前缀1010010(第10个节点),它在BT中对应的位为1,所以我们继续检查前缀10100100,即遍历到第20个节点,对应的位也为1。因为第20个节点是叶子节点,所以验证返回true,报告当前子范围以及目标范围不为空。在本例中,REncoder 仅查询RBF一次,而Rosetta需要查询布隆过滤器5次,因此 REncoder 的性能应该几乎是 Rosetta的5倍。
2.4 通过选择存储级别进行FPR优化
一个很自然的问题出现了:应该在RBF中存储线段树的多少级?也就是说,每个键应该存储多少个前缀?对于大小为64位的键,如果存储它们的所有64个前缀,所需的空间将是非常大的。因此必须做一个权衡,只存储每个键部分前缀。
在验证阶段,前缀的查询从能够精确覆盖子范围内所有键的前缀开始,这意味着之前的前缀将不会被查询。显然,当最大范围查询大小为Rmax时,只需要存储最后的log2Rmax +1个前缀。在实验过程中,论文发现当给定内存时:在某些数据集中,仅存储最后的log2Rmax +1个前缀仍然占用过多的空间,导致FPR较高;在其他数据集中,最后log2Rmax +1个前缀只占用很少的空间。这种情况下可以存储更多的前缀,并对其进行额外的查询,以进一步降低FPR,例如,对于范围[10100000, 10100011],在查询前缀101000之前,依次查询前缀1, 10, 101, 1010, 10100。因此,如何针对不同的数据集自适应地选择存储级别的数量Ls是优化FPR的关键。
虽然RBF与标准布隆过滤器并不完全相同,但它们具有一些共同的特征,例如当布隆过滤器的位数组中1的比例(P1)接近0.5时,FPR几乎是最低的。由于位数组的长度和哈希函数的数量确定,P1仅与插入的键的数量(ni)有关。给定一个包含n个不同键的数据集,无论键分布如何,标准布隆过滤器的ni都是n(标准布隆过滤器仅插入键本身)。REncoder还插入了键的多个前缀,因此它的ni与键分布和每个键要插入的前缀数量(即存储的级别数 Ls)有关。
例如,给定两个不同的数据集A{000、001、010}、B{000、010、100}。我们将A和B的REncoder的ni分别表示为An和Bn。当 Ls为1时,An为3({000、001、010}),Bn为3({000、010、100})。当 Ls为2时,An为5({000、0001、010、00、01}),Bn为6({000、010、100、00、01、10})。当 Ls为3时,An为6({000、001、010、00、01、0}),Bn为8({000、010、100、00、01、10、0、1})。假设当ni为6时,P1接近于0.5(FPR是最低的)。为了实现最优FPR,REncoder需要为数据集A存储3级,为数据集B存储2级。在实际应用中,计算ni和相应的P1是耗时的。因此可以在插入过程中逐渐增加Ls,直到ni接近最优值(P1接近0.5)。具体地说,论文按轮插入键的前缀。在每一轮中只插入每个键的最后nr个前缀。插入结束于P1接近0.5的轮。请注意,nr(每一轮中每个键插入的前缀数)可以根据不同的需要进行设置:设置大以获得更好的插入性能,设置小以获得更好的查询性能。
另一个问题是:存储一定要从最低层开始吗?答案是不。仍以数据集B{000、010、100}为例。无需存储最低级别 ({000,010,100}),因为倒数第二级别 ({00,01,10}) 足以区分所有键。这意味着可以从更高的层次开始存储更重要的信息。因此,论文提出REncoderSS。在插入键之前,REncoderSS 会计算每对键之间的最长公共前缀 (LCP) 的长度的最大长度(记为lkklcp)。REncoderSS从第lkklcp+1级开始存储,这足以区分所有的键。通常情况下,REncoderSS的FPR值低于REncoder。但在相关的工作负载中,REncoder的FPR与SuRF一样显著增加,这是因为没有较低的级别。为了弥补REncoderSS的这个缺点,论文提出了REncoderSE。REncoderSE在插入之前需要对一些查询进行采样。采样后,REncoderSE不仅计算lkklcp,还计算每对键-查询之间的LCP的最大长度(表示为lkqlcp)。低于lkqlcp的级别是必要的,因为只有它们才能区分某些存储的键和查询。因此,当lkqlcp≤lkklcp时,REncoderSE从lkklcp+1级别开始存储,就像REncoderSS。当lkqlcp>lkklcp时,REncoderSE从lkqlcp+1级开始存储,但方向相反。在这种情况下,lkqlcp+1级被视为最终级。通过存储必要的级别(低于lkqlcp的级别),REncoderSE在相关的工作负载中保持较低的FPR。
三.实验
论文比较了三种版本的REncoder与最先进的范围布隆过滤器:SuRF、Rosetta和SNARF。所有实验均基于LSM树进行。
论文在一台拥有18核CPU(36个线程,英特尔CPU i9-10980XE @3.00 GHz)的服务器上运行实验,它有128GB内存。该操作系统是Ubuntu版本18.04 LTS。所有的算法都在C++中实现,并由g++ 9.3.0和-O2选项构建。论文使用的哈希函数是带有随机初始种子的32位Bob哈希。同时使用SIMD来加速在RBF中插入/提取一个位图的过程。
3.1 数据集和实验设置
合成数据集:合成数据集包含50M的64位整数键。
SOSD数据集: SOSD 是一个针对学习索引的基准测试。它包含四个真实的数据集: amazon.com的图书销售数据,Facebook的用户身份数据,开放街道地图的统一采样数据以及维基百科文章的编辑时间戳。所有这些数据集都包含200M的64位整数键。论文随机地从每个数据集中抽取10M键进行实验。
工作负载:论文生成四种类型的查询:范围2∼32和2∼64的范围查询、相关范围查询和点查询。每种类型的查询的数量是10M。对于2∼32范围查询,论文从均匀分布中生成10M的整数键作为范围查询的左边界,然后从2到32中随机选择一个整数作为每个查询的范围大小。2∼64范围查询和点查询与2∼32范围查询思路相同,点查询的范围大小设置为1。对于相关范围查询,论文从数据集中随机选择10M个键,然后将这些键增加32并将它们设置为范围查询的左边界,相关范围查询的范围大小是从2到32之间随机选择的。对于每个真实数据集,论文生成1M个真实范围查询。然后从剩下的190M个键中随机选择1M个键设置为范围查询的左边界。
3.2 度量指标
假阳率(FPR): FPR测量范围过滤器的准确性。FPR是指被错误地报告为阳性的阴性数据与所有阴性数据的比例。
过滤器吞吐量:过滤器吞吐量测量范围过滤器的探测速度。它的单位是每秒数百万次操作。(Mops/s)。
总体吞吐量:总体吞吐量使用范围过滤器来测量查询的探测速度。在实验中,我们构建了一个具有两级存储的仿真环境。范围过滤器存储在第一层,而元素(键值对)存储在第二层。当查询出现时,我们在第一级查询范围过滤器,只有当范围过滤器返回正时,我们才访问第二级。总体吞吐量衡量了整个过程的速度。它的单位与过滤器吞吐量相同。
3.3 成本与收益的实验
论文在模拟环境中比较REncoder和LSM树的默认过滤器(布隆过滤器),以展示在LSM树中使用REncoder的成本和增益。论文使用合成数据集和2~32范围查询。布隆过滤器通过依次检查范围内所有键的存在来处理范围查询。实验结果表明,使用REncoder的构建的速度略慢一点,但增益要快得多。
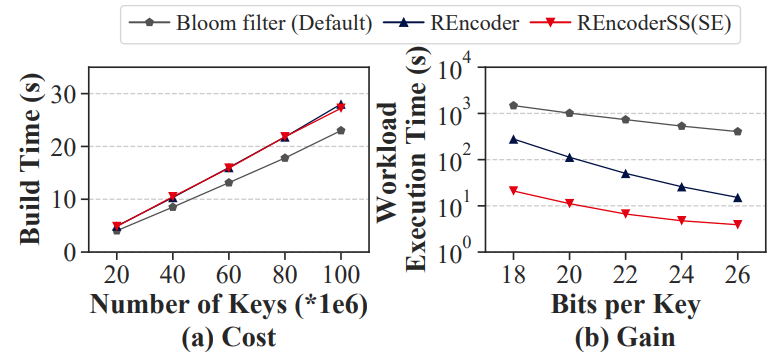
图3 在LSM树中使用REncoder的成本和收益
构建时间(图3(a)):无论键的数量如何变化,REncoder的构建时间只比布隆过滤器稍慢一些。因为对于每个键,Bloom flter只插入键本身,而REncoder要插入键的若干个前缀。然而,REncoder可以通过使用位图和RBF同时插入多个前缀,从而加速了它的构建,以达到与布隆过滤器相当的效率(82%)。与查询性能的增益相比,构建的时间成本可以忽略不计。
工作量执行时间(图3(b)):REncoder的执行时间比布隆过滤器快得多,当BPK较小时更显著。REncoder的执行时间几乎比所有bpk上的布隆过滤器快一个数量级(平均快15倍)。原因如下: 1) 布隆过滤器需要按顺序检查范围内所有键的存在,这导致了许多内存访问和哈希操作。相比之下,REncoder只需要更少的内存访问(通常是一次),这要归功于对线段树和布隆过滤器查询的局部性的使用。这意味着REncoder比布隆过滤器具有更好的吞吐量;2)与布隆过滤器相比,再编码器的FPR更低,导致I/O更少,这在执行时间中起着很大的作用。
总时间(图 4):尽管构建速度较慢,使用REncoder进行查询的总时间仍然比布隆过滤器快得多(11倍),REncoderSS(SE)甚至更好(平均快34倍)。构建范围过滤器的开销可能会被查询性能的提高所掩盖。

图4 布隆过滤器和REncoder的总时间。
3.4 范围查询实验
论文使用合成数据集比较了2∼32范围查询和2∼64范围查询中范围过滤器的性能。
FPR(图5):无论BPK如何变化,REncoder(SS/SE)的FPR都是所有范围过滤器中最低的或与最低的相当。
过滤器吞吐量(图6(a)-(b)):无论BPK如何变化,REncoder(SS/SE)的过滤器吞吐量远远优于Rosetta,可与SuRF相当。
总体吞吐量(图6(c)-(d)):无论BPK如何变化,REncoder(SS/SE)的总体吞吐量都高于SuRF和Rosetta。
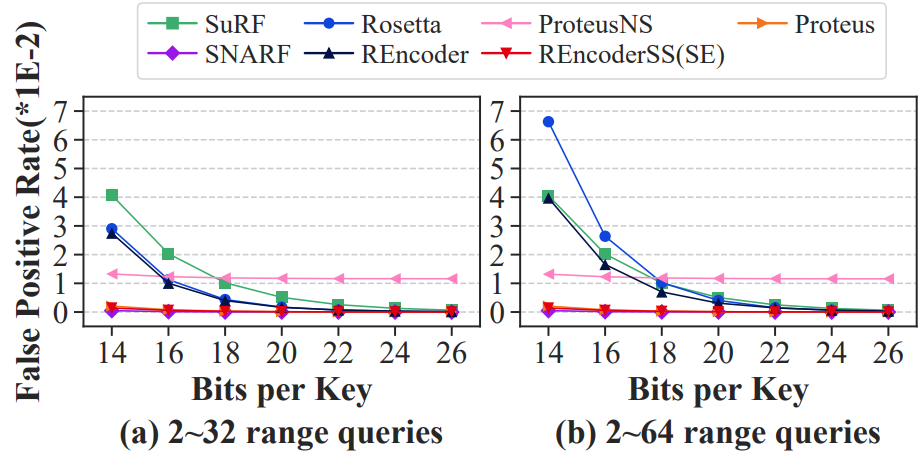
图5 范围查询的FPR
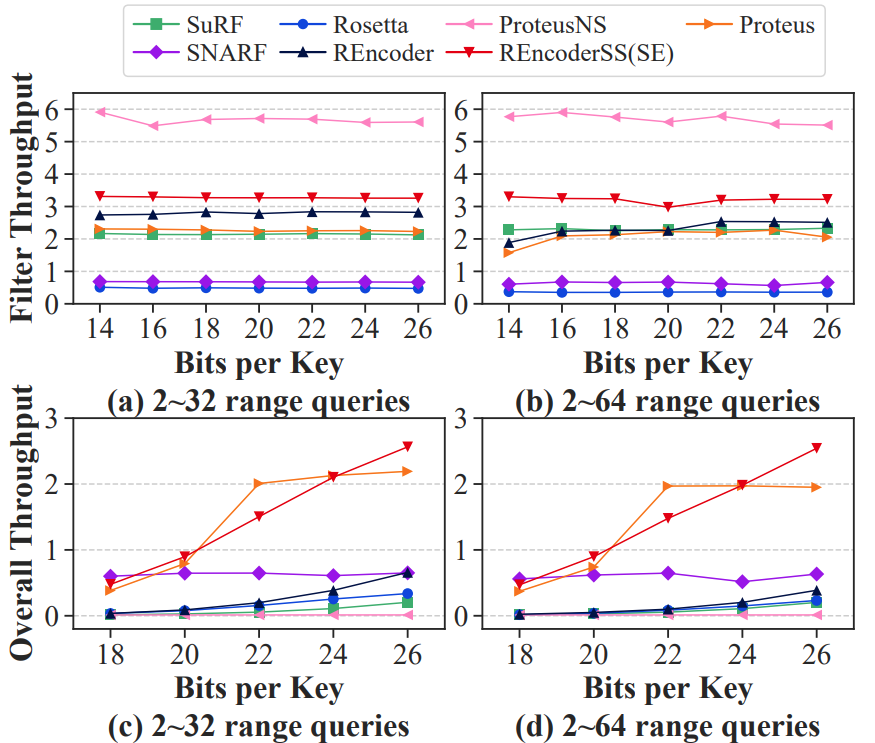
图6 范围查询的吞吐量
分析:SuRF截断较低级别的部分节点以节省空间,这可能导致范围查询的重要信息丢失。而Rosetta和REncoder通过布隆过滤器保留这些信息,并使用额外的查询来进一步保证信息的准确性。因此,Rosetta和REncoder的FPR比SuRF要低得多。SuRF的过滤器吞吐量比Rosetta好得多,因为它在内部使用了一个截断的trie。当范围查询到来时,SuRF只需要在简洁的trie中遍历,而Rosetta需要对布隆过滤器执行许多耗时的查询。相比之下,REncoder利用对布隆过滤器的查询局部性来实现比Rosetta更高的过滤器吞吐量,同时保持较低的FPR。总体吞吐量表明了实际应用中的性能。由于一级存储(如内存)的计算速度比二级存储(如磁盘)的数据获取速度快得多,尽管SuRF具有更高的过滤器吞吐量,但由于其较高的FPR导致在二级存储中产生更多不必要的数据获取,它的总体吞吐量受到影响。相比之下,Rosetta和REncoder具有更高的总体吞吐量,这要归功于它们较低的FPR。另一方面,一级存储中的计算在总体吞吐量中仍然起着不可忽视的作用。因此,REncoder比Rosetta具有更高的总体吞吐量,因为它在一级存储中具有更好的性能。SNARF通过使用学习模型实现了低FPR,但对压缩位数组的查询严重限制了过滤器吞吐量。Proteus同时具有较低的FPR和较高的过滤器吞吐量。因为CPFPR模型通过抽样查询进行了优化。然而,当禁止采样查询时,使用默认设计的Proteus(即ProteusNS)的FPR比REncoder要差得多。由于键和查询都是均匀分布的,因此REncoderSS可以实现与REncoderSE相同的性能,我们将它们表示为REncoderSS(SE)。与REncoder相比,REncoderSS(SE)存储更高的级别,包含更多重要的信息,所以有更低的FPR和更高的过滤器吞吐量。REncoderSS(SE)在所有BPK范围中具有最高的总体吞吐量(除22个之外)。
3.5 点查询实验
论文用合成数据集比较点查询中范围过滤器的性能。
FPR(图7(a)):REncoder(SS/SE)在所有BPK设置的点查询中保持低FPR。
过滤器吞吐量(图7(b)):REncoder(SS/SE)的过滤器吞吐量略低于Rosetta。
分析:与范围查询相比,在点查询中SuRF、Rosetta和的REncoder的FPR显著降低。对于SuRF,它的散列键的后缀提供了额外的可靠信息来帮助降低点查询的FPR的。对于Rosetta和REncoder,它们在点查询中对布隆过滤器的查询比在范围查询中需要的查询少,因此它们的FPR较低。另一方面,与范围查询相比,SuRF、Rosetta 和 REncoder 在点查询中的过滤器吞吐量有所增加。对于SuRF来说,与范围查询相比,点查询对其内部尝试的遍历要简单得多,这大大缩短了查询的延迟。Rosetta和REncoder对布隆过滤器的查询较少,从而减少了哈希计算并提高了整体性能。SNARF和Proteus在点查询中的表现与在范围查询中的表现类似,因为它们的结构对于不同的范围大小都很稳健。
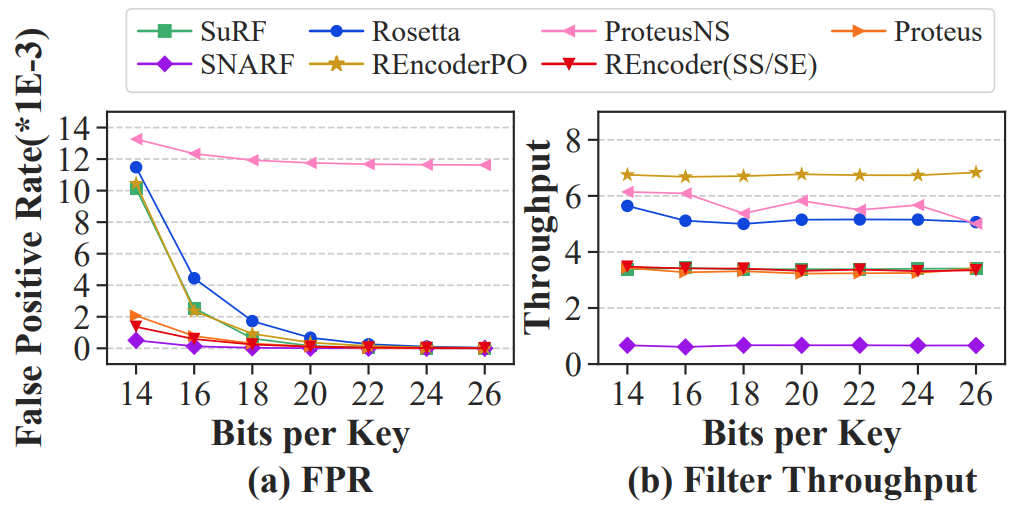
图7 点查询的性能。
优化:由于Rosetta只查询最低级别的布隆过滤器,因此它比REncoder具有更高的过滤器吞吐量。受 Rosetta 的启发,论文提出了一个用于点查询的REncoder的优化版本,称
为 REncoderPO,它仅查询键的最长前缀(即键本身)以获得更高的过滤吞吐量,但代价是更差的FPR。Rosetta、REncoder和REncoderPO的整体吞吐量如图8所示。当BPK<26 时,所有过滤器的 FPR 都较高,因此整体吞吐量以二级存储中的查询为主。
REncoder由于其最低的FPR而具有最高的总体吞吐量。
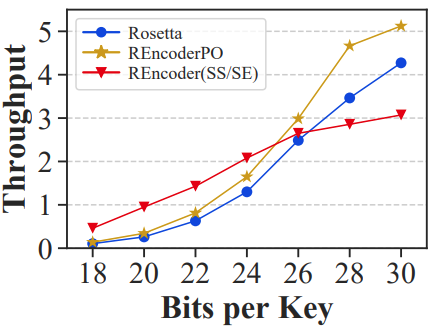
图8 点查询的总体吞吐量
3.6 在相关查询上的实验
论文使用合成数据集比较相关查询中范围过滤器的性能。
FPR(图9(a)):在所有的BPK设置中,REncoder(SE)在相关查询中保持较低的FPR。过滤器吞吐量(图9(b)):在所有BPK设置的相关查询中REncoder(SE)比Rosetta具有更高的过滤器吞吐量。
分析:即使当BPK为26时,SuRF的FPR也达到了1。原因是SuRF截断了较低级别的部分节点,而截断的节点包含用于区分查询键和类似的存储键的重要信息。Rosetta和REncoder几乎不受查询分布的影响,原因是它们都使用布隆过滤器来存储键。即使两个键高度相似,经过哈希后,它们也完全不同。另一方面,当关联查询到来时,SuRF通常需要遍历到trie的底层,这非常耗时,因此它的过滤器吞吐量略有下降。与FPR类似,Rosetta 和 REncoder 的过滤器吞吐量也不受影响。除了SuRF之外,SNARF、ProteusNS和REncoderSS的FPR也达到1。SNARF的学习模型无法区分高度相似的键和查询。至于ProteusNS和REncoderSS,虽然它们都使用布隆过滤器,但它们不存储线段树的较低层。因此,他们无法区分相似的键和查询。

图9 相关查询的性能
3.7 真实数据集的范围查询实验
论文比较了范围过滤器在真实数据集的范围查询中的性能。
FPR(图10(a)-(d)):REncoder(SS/SE)在所有数据集中具有最低或接近最低的FPR。过滤器吞吐量(图10(e)-(f)):在所有数据集中,REncoder(SS/SE)的过滤器吞吐量比Rosetta更高。
分析: REncoder可以自适应地选择段树中存储的级别Ls的数量,即根据数据集进行空间分配。因此,它在所有数据集上的FPR都较低。REncoderSS(SE)的FPR低于REncoder,特别是在相对不倾斜的数据集(amzn和osmc)。这是因为在这样的数据集中,键和查询几乎是均匀分布的,这使REncoderSS(SE)能够比REncoder存储更高的级别(更重要的信息)。REncoder和REncoderSS(SE)的过滤器吞吐量是相似的,并且在相对倾斜的数据集(face和wiki)上都有所下降。这是因为当键和查询相似时,REncoder和REncoderSS(SE)需要增加查询布隆过滤器的次数来区分它们。总之,REncoder(SS/SE)在所有真实数据集上具有更好的的FPR和过滤器吞吐量。
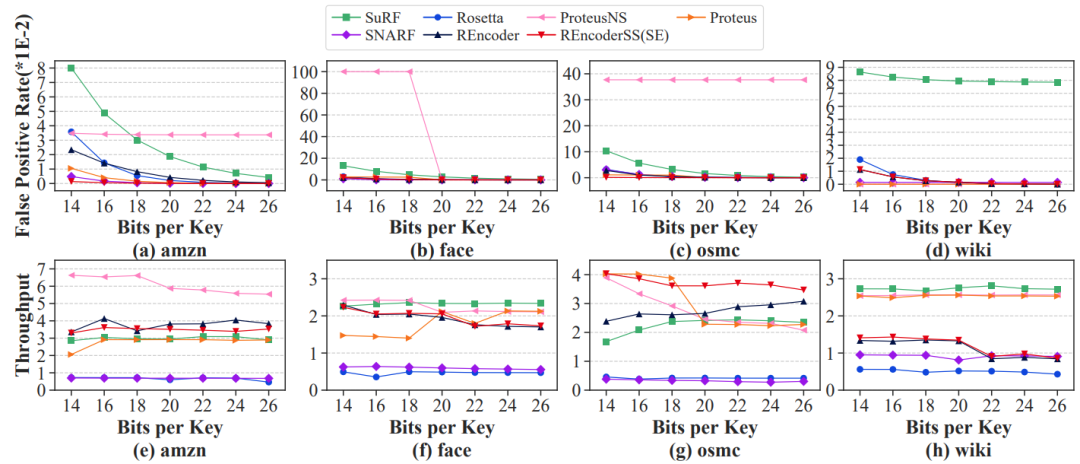
图10 对真实数据集的范围查询的性能
四.总结
论文介绍了一种新型的具有较高时空效率和精度的范围过滤器。其关键思想是利用局部性在不影响准确性的情况下加速查询。它有理论上的误差界限,并支持各种工作负载。实验结果表明, REncoder 与现有的过滤器相比具有一定的优越性。
主要研究方向:时空数据管理 |
|







