关于机器学习-基于2023年度各省统计数据的降维后再Kmean聚类

在机器学习中，PCA（主成分分析）和K-Means聚类是两种非常实用的技术，尤其在数据预处理和无监督学习中。PCA是一种降维方法，通过减少数据集的特征数量来简化数据，同时保留大部分的变异性。这有助于我们更好地理解和分析数据。K-Means则是一种聚类算法，能够将数据分成几个不重叠的群组或“簇”。这种算法常用于发现数据的内在结构和模式。

KMeans聚类前进行降维的主要原因是为了提高算法的效率和效果‌。降维可以减少数据的维度，从而减少计算量，加快聚类速度。此外，降维还能去除冗余信息，使数据更加简洁，有助于发现数据的内在结构和规律‌。

降维对KMeans聚类的影响包括：

‌提高计算效率‌：降维可以显著减少数据的维度，从而减少计算量和存储空间的需求。KMeans算法的时间复杂度与数据维度和数据量密切相关，降维可以显著降低计算复杂度，加快聚类速度‌

‌改善聚类效果‌：在某些情况下，高维数据可能存在冗余或无关的特征，这些特征可能会干扰聚类过程，导致聚类效果不佳。通过降维去除这些特征，可以使聚类结果更加准确和有意义‌

‌减少噪声影响‌：高维数据中可能包含大量的噪声数据，降维可以通过聚合相似数据点来减少噪声的影响，从而提高聚类的稳定性‌

第一段代码同以前，不再赘述

import pandas as pd # panda库
from sklearn.preprocessing import StandardScaler # 标准化库
from sklearn.cluster import KMeans  # 导入sklearn聚类模块
from sklearn.metrics import silhouette_score   # 效果评估模块
from sklearn.decomposition import PCA

# 替换为你的文件路径
data_path = r'E:\JetBrains\PythonProject\DeepLearning\provicedata.csv'
df = pd.read_csv(data_path)
# 选择特征列
features = ['GDP', 'Primary industry', 'Primary industry','Primary industry',
            'resident population','population growth rate',
            'import and export','export value','import value',
            'General budget revenue','General budget expenditure',
            'Per capita disposable income','Per capita consumption expenditure','area']  # 替换为你的特征列名
X = df[features]
n_samples, n_features = X.shape
print('样本数：%d , 特征数：%d' % (n_samples, n_features))

# 数据归一化
scaler = StandardScaler()
scalerX = scaler.fit_transform(X)

K-Means算法中的explained_variance_ratio_‌是指每个主成分解释的方差占总方差的比率。在PCA（主成分分析）中，explained_variance_ratio_用于衡量每个主成分对数据变异的解释程度。具体来说，PCA通过正交变换将原始数据转换为一组新的变量（即主成分），这些主成分按方差大小排序，其中第一个主成分解释的方差最大，第二个次之，依此类推。explained_variance_ratio_则是每个主成分解释的方差占总方差的百分比，通常用于确定需要保留的主成分数量。

在这里我们通过比较选前两个主成分即可，占比在85%。

# PCA降维
for i in range(2,5):
    # 1.components_ ：特征空间中的主轴，表示数据中最大方差的方向。组件按排序 explained_variance_
    # 2.explained_variance_：它代表降维后的各主成分的方差值。方差值越大，则说明越是重要的主成分
    # 3.explained_variance_ratio_：它代表降维后的各主成分的方差值占总方差值的比例，这个比例越大，则越是重要的主成分
    # 4.singular_values_：每个特征的奇异值，奇异值等于n_components 低维空间中变量的2范数
    # 5.mean_：每个特征的均值
    # 6.n_components_：即是上面输入的参数值
    # 7.n_features_：训练数据中的特征数量
    # 8.n_samples_：训练数据中的样本数
    # 9.noise_variance_：等于X协方差矩阵的（min（n_features，n_samples）-n_components）个最小特征值的平均值
    pca = PCA(n_components=i)
    pcaX = pca.fit_transform(scalerX)
    print("For n_components={}, The PCA explained_variance_ratio_ is {}".format(i, pca.explained_variance_ratio_))
    # For n_components=2, The PCA explained_variance_ratio_ is [0.54113074 0.30908829]
    # For n_components=3, The PCA explained_variance_ratio_ is [0.54113074 0.30908829 0.06978044]
    # For n_components=4, The PCA explained_variance_ratio_ is [0.54113074 0.30908829 0.06978044 0.04070103]

pca = PCA(n_components=2)
pcaX = pca.fit_transform(scalerX)

将聚类后的结果写入相应字段

for k in range(3,6):
    # 模型训练
    KmeansModel = KMeans(n_clusters=k, random_state=42)
    KmeansModel.fit(pcaX)
    # 计算轮轴系数：
    # 轮廓系数用于计算每个样本的平均簇内距离a(样本i到同簇其他样本的平均距离，ai值越小说明该样本越应该被聚到该类，即簇内不相似度)和平均邻近簇距离b(样本i到其他相邻簇的所有样本的平均距离bi，bi越大说明样本i越不属于其他簇，即簇间不相似度)。
    # 每个样本的轮廓系数计算公式为：(b-a)/Max(a,b)，轮廓系数越接近1说明结果越好（聚类越准确），越接近-1说明结果越差，若值在0值附近，则说明样本在两个簇的边界上
    score = silhouette_score(pcaX, KmeansModel.labels_, metric='euclidean')
    print("For n_clusters={}, The Silhouette Coefficient is {}".format(k, score))
    # 合并数据和特征
    kmeans_labels = pd.DataFrame(KmeansModel.labels_, columns=['scaler pca kmean labels'+str(k)])
    df = df.join(kmeans_labels)
df.to_csv('provicedatav3.csv', index=False, header=True, encoding='utf-8'

最后一段代码同以前，不再赘述

import matplotlib.pyplot as plt
import cartopy.crs as ccrs
import cartopy.feature as cfeature
import geopandas as gpd
import pandas as pd

pd.set_option('display.max_columns', None)
# 显示所有行
pd.set_option('display.max_rows', None)
# 不换行显示
pd.set_option('display.width', 1000)
# 行列对齐显示，显示不混乱
pd.set_option('display.unicode.ambiguous_as_wide', True)
pd.set_option('display.unicode.east_asian_width', True)
# 显示精度
pd.set_option('display.precision', 4)
# 显示小数位数
pd.get_option("display.precision")

# 加载中国各省的地理数据
# 你需要从网上下载中国各省的shapefile文件，例如从GADM (https://gadm.org/download_country_v3.html)
china = gpd.read_file(r'E:\shp\china\中国_省_Areas.shp')
print(china.head())
# 加载九段线数据,九段线数据可以从自然资源部或其他公开数据源获取
nine_dash_line = gpd.read_file(r'E:\shp\china\中国_省_Lines.shp')
# 加载上次另存的数据
data_path = r'E:\JetBrains\PythonProject\DeepLearning\Sklearn\provicedatav3.csv'
df = pd.read_csv(data_path)
# 将kmean label3、kmean label4 、kmean label5
china['scaler pca kmean labels3'] = china['name'].map(df.set_index('city')['scaler pca kmean labels3'])
china['scaler pca kmean labels4'] = china['name'].map(df.set_index('city')['scaler pca kmean labels4'])
china['scaler pca kmean labels5'] = china['name'].map(df.set_index('city')['scaler pca kmean labels5'])

def drawchina(df,columnname):
    # 创建地图
    fig = plt.figure(figsize=(12, 8))
    ax = fig.add_subplot(1, 1, 1, projection=ccrs.PlateCarree())
    # 设置地图范围为中国（包括南海区域）
    ax.set_extent([73, 135, 3, 54], crs=ccrs.PlateCarree())
    # 添加地理特征
    ax.add_feature(cfeature.COASTLINE.with_scale('50m'))
    ax.add_feature(cfeature.BORDERS.with_scale('50m'), linestyle=':')
    ax.add_feature(cfeature.LAND.with_scale('50m'), edgecolor='black')
    ax.add_feature(cfeature.OCEAN.with_scale('50m'))
    ax.add_feature(cfeature.LAKES.with_scale('50m'))

    # 绘制各省地图并根据数据着色
    df.plot(column=columnname, ax=ax, legend=True, cmap='OrRd', legend_kwds={'label': "Data by Province"})
    # df.plot(column=columnname, ax=ax, linewidth=2,legend_kwds={'label': "Data by Province"})
    # 绘制九段线
    nine_dash_line.plot(ax=ax, color='blue', linewidth=2, label='Nine-Dash Line')
    plt.legend()
    # 添加标题
    plt.title('China Provinces Data with Nine-Dash Line')
    # 显示地图
    plt.tight_layout()
    plt.show()

drawchina(china, 'scaler pca kmean labels3')
drawchina(china, 'scaler pca kmean labels4')
drawchina(china, 'scaler pca kmean labels5')

可视化呈现结果，自己品就行了

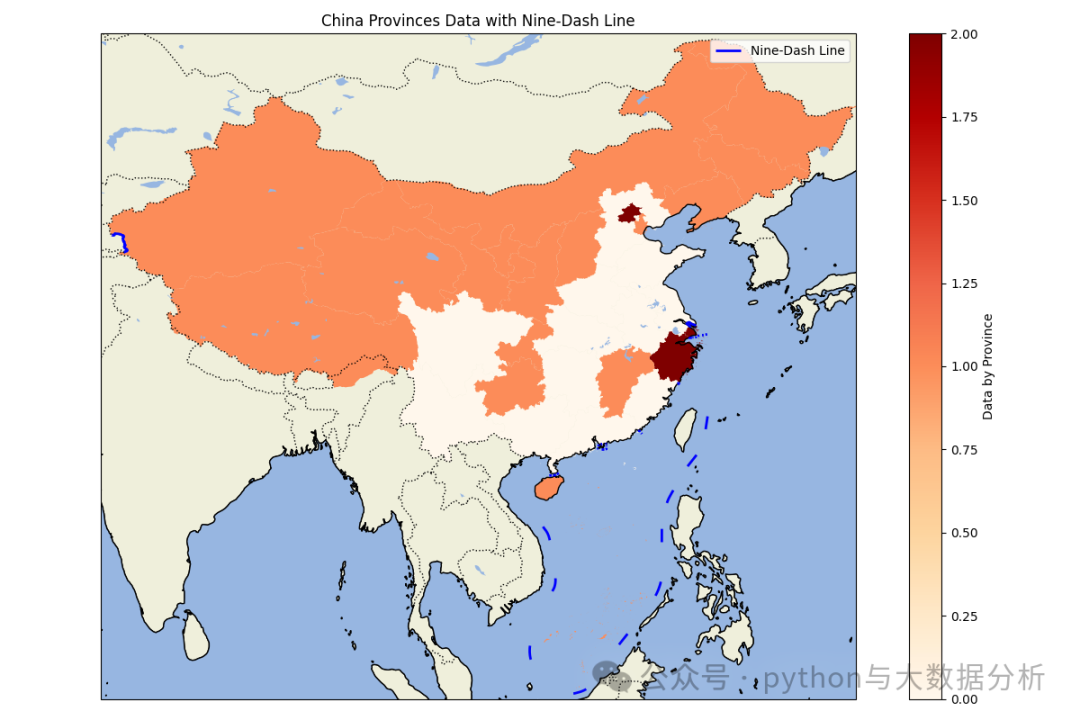
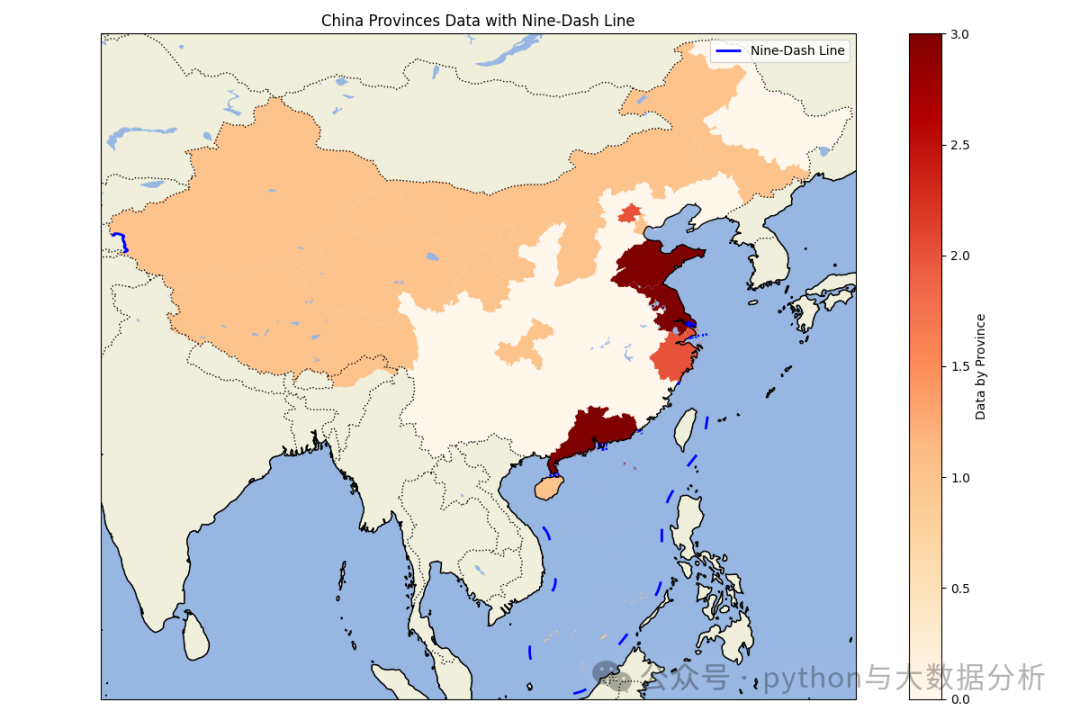
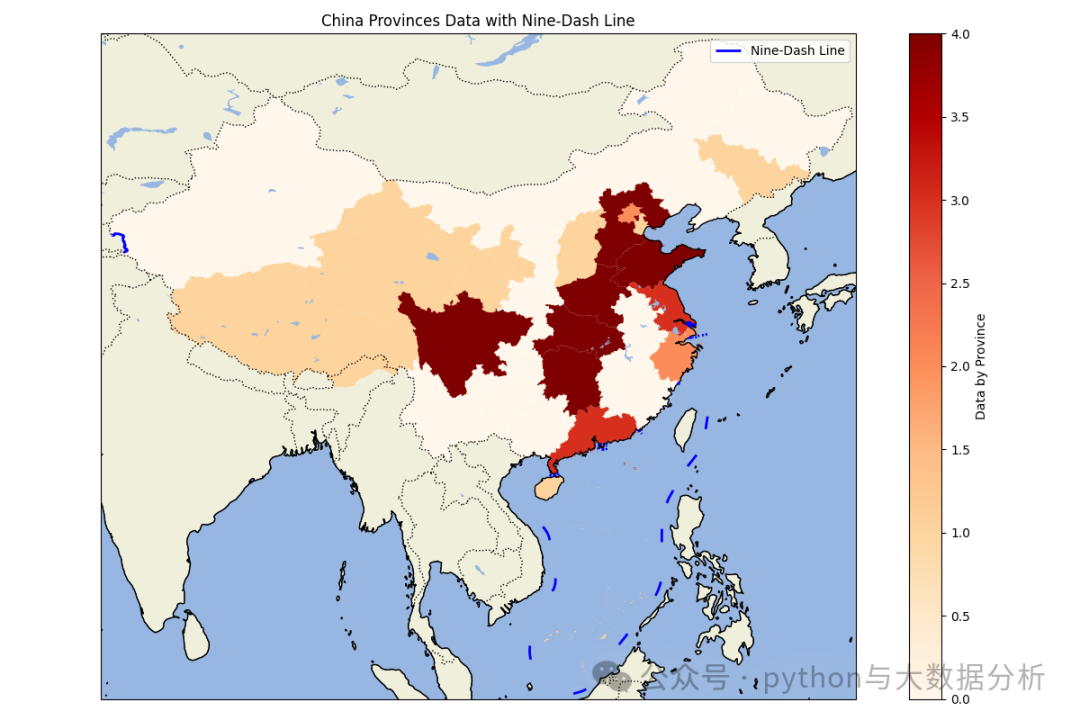
最后欢迎关注公众号：python与大数据分析