向量数据库可能听起来很高深,但其实它的概念可以用简单的语言来解释。在这篇文章中,我们将一步步了解什么是向量数据库,它是如何工作的,以及它在日常技术应用中的重要性。
什么是向量?
首先,让我们从“向量”这个词说起。在数学中,向量是用来表示方向和大小的量,你可以将其想象成一个带方向的箭头。在计算机科学中,向量用于表示数据,可以是任何东西,比如一段文字、一张图片或者一首歌的特征。

数学中的向量
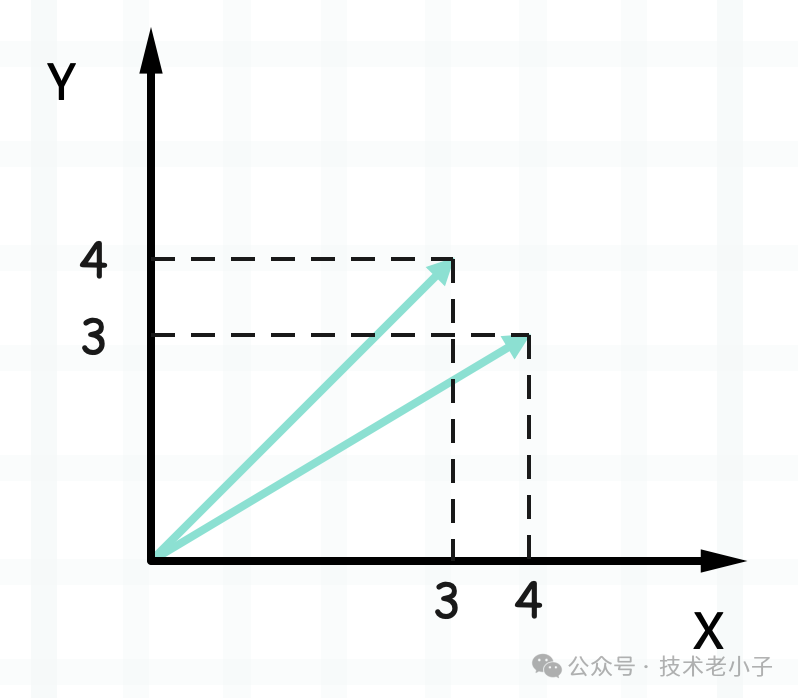
在数学中,向量通常表示为带方向的线段。它有两个主要的属性:方向和大小(或长度)。例如,一个二维空间中的向量可以用来表示从点A到点B的距离和方向。如果我们有向量 𝑣=(3,4)v=(3,4),它意味着从原点(0,0)出发,你需要向东(或右)移动3个单位,向北(或上)移动4个单位来到达终点。
计算机科学中的向量
在计算机科学中,尤其是在处理数据和机器学习模型时,向量通常用来表示数据点的特征集合。这些向量可能代表多种类型的数据:
文本数据: 文本可以通过各种技术转换成数值向量,这些技术包括词袋模型、TF-IDF、Word2Vec等。例如,假设我们有三个文本:“apple”,“banana”,和“fruit”。我们可以将这些文本转换为向量,如 𝑎𝑝𝑝𝑙𝑒=(1,0,0) ,𝑏𝑎𝑛𝑎𝑛𝑎=(0,1,0) ,𝑓𝑟𝑢𝑖𝑡=(0,0,1) ,每个位置代表一个特定的词在文本中的出现。
图像数据: 图像可以通过提取颜色、纹理、形状等特征转换为向量。例如,一个简单的灰度图像可以被转换为一个向量,其中每个元素代表一个像素的灰度值。
音频数据: 音频文件可以通过特征如频率分布、音量等转换为向量。
实际应用示例
假设我们正在开发一个推荐系统,需要推荐电影给用户。每部电影可以通过多个特征来描述,如类型、导演、演员、电影时长等。我们可以将每部电影表示为一个向量,其中每个元素代表一个特定的特征。例如,电影《泰坦尼克号》可能被表示为一个向量 𝑡𝑖𝑡𝑎𝑛𝑖𝑐=(0,0,1,0,...,1),其中向量的每个位置代表一种类型(如动作、喜剧、爱情等),以及其他相关的特征。
通过将数据转换为向量,我们可以使用各种算法(如余弦相似度、欧几里得距离等)来计算不同电影之间的相似性,从而为用户推荐相似的电影。这种方法在许多现代技术应用中非常普遍,是数据处理和机器学习的基础。
数据向量化是什么
数据向量化是将各种形式的数据转换成向量(数值数组)的过程,这一过程在机器学习、数据分析和其他计算领域中至关重要。向量化的数据可以被计算机程序更有效地处理和分析,因为大多数算法(尤其是机器学习算法)在数值数据上操作效率更高。
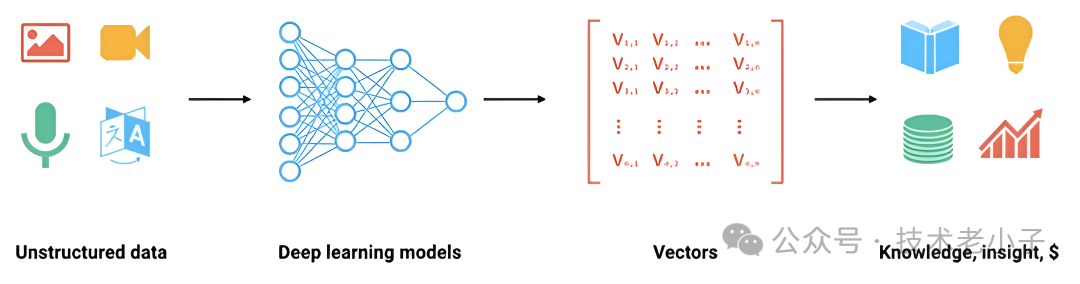
数据向量化的主要过程包括:
特征提取: 根据数据的类型(如文本、图像、音频等),提取能够代表数据特性的信息。例如,对于文本数据,可以提取词频、关键词等;对于图像数据,可以提取颜色、边缘、纹理等信息。
编码和标准化: 将提取的特征转换为数值形式,并进行标准化处理以适应不同的算法要求。例如,在处理文本数据时,常用的编码方法包括词袋模型、TF-IDF等。
维度选择: 根据需要选择重要的特征维度,以减少数据的复杂性和提高处理效率。这一步通常涉及特征选择或降维技术,如主成分分析(PCA)。
相似度计算
相似度计算是一种衡量两个数据项之间相似程度的技术,广泛应用于数据分析、机器学习、信息检索等领域。根据数据的类型和应用场景,可以选择不同的相似度计算方法。以下是几种常见的相似度计算方法:
1. 欧氏距离 (Euclidean Distance)
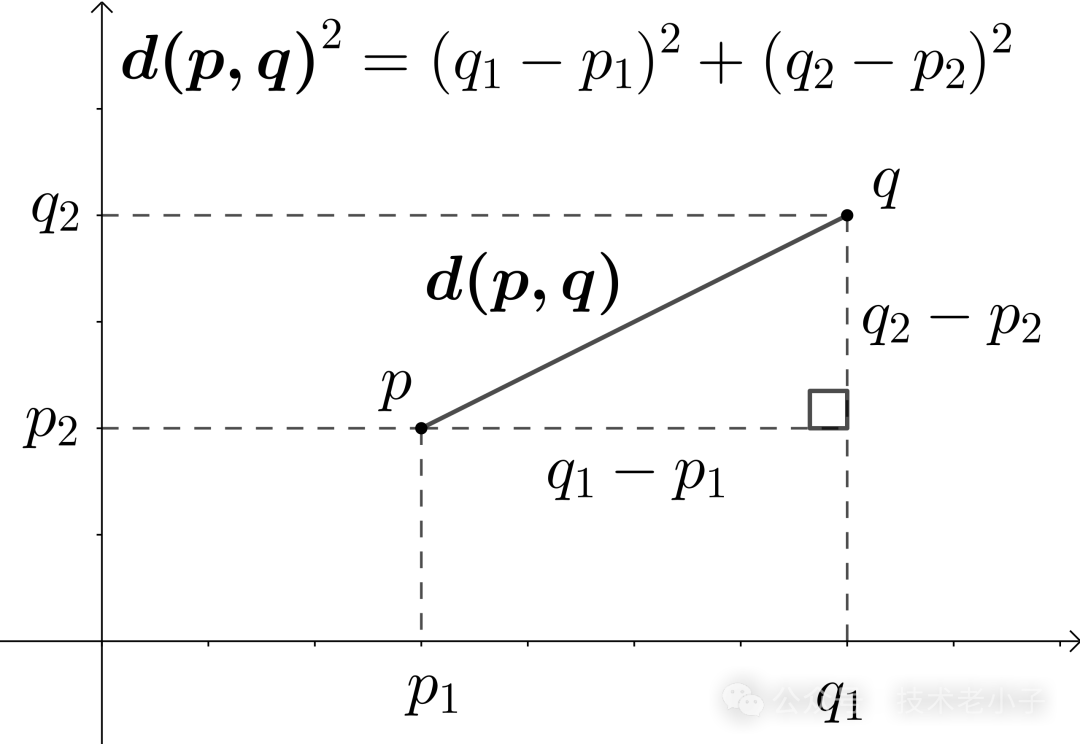
定义: 欧氏距离是最直观的距离度量方式,它是两点间的直线距离。
计算公式: 𝑑(𝑝,𝑞)=∑𝑖=1𝑛(𝑝𝑖−𝑞𝑖)2d(p,q)=∑i=1n(pi−qi)2
应用: 常用于连续数值数据的相似度计算,如在聚类分析中的K-means算法。
2. 余弦相似度 (Cosine Similarity)
定义: 余弦相似度通过测量两个向量的夹角的余弦值来评估它们的相似度。它不受向量长度的影响,只与向量方向有关。
计算公式: cos(𝜃)=𝑝⋅𝑞∥𝑝∥∥𝑞∥cos(θ)=∥p∥∥q∥p⋅q
应用: 广泛用于文本分析中,如计算文档或单词向量的相似度。
3. 曼哈顿距离 (Manhattan Distance)
定义: 曼哈顿距离是根据格子化城市中的街区距离来定义的,即两点在标准坐标系上的绝对轴距总和。
计算公式: 𝑑(𝑝,𝑞)=∑𝑖=1𝑛∣𝑝𝑖−𝑞𝑖∣d(p,q)=∑i=1n∣pi−qi∣
应用: 在某些情况下,如城市街道布局的规划,曼哈顿距离比欧氏距离更实用。
4. 杰卡德相似度 (Jaccard Similarity)
定义: 杰卡德相似度衡量的是两个集合交集和并集的比例。
计算公式: 𝐽(𝐴,𝐵)=∣𝐴∩𝐵∣∣𝐴∪𝐵∣J(A,B)=∣A∪B∣∣A∩B∣
应用: 常用于比较样本集合的相似度,如用户购买行为分析。
5. 汉明距离 (Hamming Distance)
定义: 汉明距离是两个字符串同一位置的不同字符的数量,它衡量了两个字符串之间的差异。
计算公式: 对于两个等长字符串,汉明距离是对应位置上不同字符的数量。
应用: 在信息编码(如错误检测和校正码)中非常重要。
向量数据库是什么?
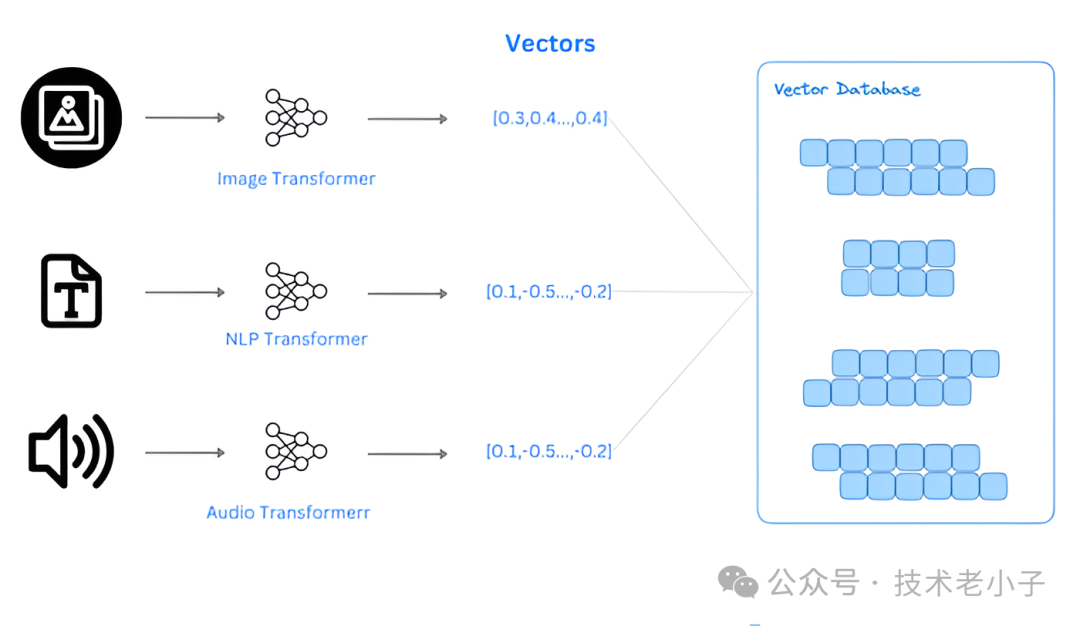
向量数据库,顾名思义,是一种专门用来存储和处理向量数据的数据库。它不同于传统的数据库,传统数据库存储的是文字和数字等标准数据。向量数据库则是存储那些被转换成向量的数据,这种转换通常通过使用机器学习模型来完成。
向量数据库的工作原理
当我们把数据转换成向量后,这些向量就可以在向量数据库中存储和检索。向量数据库使用特殊的算法来快速找到与查询向量最相似的向量。这种查找过程称为“向量搜索”,它是向量数据库最核心的功能。
为什么需要向量数据库?
向量数据库在处理大规模复杂数据时非常有效。假设你正在开发一个图像搜索引擎,用户可以上传一张图片,系统则返回与之相似的图片。在这个应用中,每张图片首先通过深度学习模型(如卷积神经网络)被转换成一个高维的向量。这个向量捕捉了图片的关键特征,如颜色、形状和纹理等。
这些图片向量随后存储在向量数据库中。当用户上传一张图片时,同样将这张图片转换成一个向量,然后在向量数据库中进行快速的相似性搜索,找到与之最相似的图片向量。向量数据库能够高效地处理这种高维空间的相似性查询,迅速返回结果。
向量数据库的应用
向量数据库不仅用于图片搜索,还广泛应用于推荐系统、自然语言处理、生物信息学等多个领域。例如,在推荐系统中,向量数据库可以帮助快速匹配用户的兴趣和推荐相应的内容。

总结
向量数据库是一种强大的工具,它通过将数据转换为向量并利用高效的搜索算法来处理复杂的查询任务。对于正在迅速发展的人工智能和机器学习领域,向量数据库提供了一种有效的数据管理和检索方案。
希望这篇文章能帮助你理解向量数据库的基本概念和应用。随着技术的不断进步,了解这些新兴技术将越来越重要,也越来越有趣。






