
点击上方蓝字关注我!
如果有错误或者理解不到位的地方还请各位指正!
数据结构的相关问题,可以参考笔者写的系列数据结构文章,或者加我交流!
声明:以下内容是对清华大学出版社出版,由严蔚敏和吴伟民编著的图书《数据结构》(C语言版)的代码实现。
图书PDF版本可移步公众号【李歘歘】回复电子书领取。
上次说到了线性表的静态链表,今天我们来说一下有关栈之顺序栈,相关知识点可以先了解一下。

书中位置(页码):P44-P47
函数定义及说明:
Status InitStack(SqStack &S) //初始化栈Status Push(SqStack &S, SElemType e) //入栈void Creat(SqStack &S,int n) //创建栈,就是重复的将元素入栈(当然也可以单独写一个创建的函数)Status StackLength(SqStack S) //获取元素个数bool StackEmpty(SqStack S) //判断栈空Status GetTop(SqStack S,SElemType e) //获取栈顶元素Status Pop(SqStack &S,SElemType e) //出栈Status StackTraverse(SqStack S) //遍历--从栈底到栈顶的元素输出Status ClearStack(SqStack &S) //置空Status DestoryStack(SqStack &S) //销毁
程序代码:
#include<cstdio>#include<cstdlib>#define SElemType int#define Status int#define STACK_INIT_SIZE 100 //初始空间分配量#define STACKINCREMENT 10 //存储空间分配增量using namespace std;//栈的结构typedef struct {SElemType *base; //栈底指针,在栈结构不存在(构造之前和销毁之后),base的值为NULLSElemType *top; //栈顶指针,非空栈的栈顶指针始终在栈顶元素的的下一个位置上int stacksize; //可存储的最大容量,即最多存储的元素个数}SqStack;//初始化栈/**说明,这里使用C语言的malloc和realloc除此之外,还可以使用c++的new运算符( S.base = new SElemType[MAXSIZE];)但是,new运算符在给定一个定长数组初始化后,长度变不能改变(c++没有realloc函数)改进有两个方法,(1)、在初始化时,使用vector变长数组代替数组(2)、新建一个更大的数组,将原有的元素复制过去(realloc就是这个原理)*/Status InitStack(SqStack &S){S.base = (SElemType *)malloc(STACK_INIT_SIZE*sizeof(SElemType));if(!S.base){ //动态空间分配失败printf("动态空间分配失败\n");return 0;}S.top = S.base; //栈顶指针初值指向栈底,即top=base表示空栈S.stacksize = STACK_INIT_SIZE; //标记空间大小printf("初始化成功\n");return 0;}//入栈Status Push(SqStack &S, SElemType e){//判断栈是否满;if(S.top-S.base >= S.stacksize){ //栈满,追加S.base = (SElemType *)realloc(S.base,(S.stacksize+STACKINCREMENT)*sizeof(SElemType));if(!S.base){printf("动态空间分配失败\n");return 0;}S.top = S.base+S.stacksize; //更新栈顶元素指针S.stacksize += STACKINCREMENT; //更新最大容量}*S.top++ = e; //插入到栈顶并将栈顶指针加一printf("插入成功\n");return 0;}//创建栈,就是重复的将元素入栈(当然也可以单独写一个创建的函数)void Creat(SqStack &S,int n){InitStack(S);for(int i=0;i<n;i++){int e;scanf("%d",&e);Push(S,e);}printf("创建成功\n");}//获取元素个数Status StackLength(SqStack S){int count = S.top-S.base;return count;}//判断栈空bool StackEmpty(SqStack S){if(S.base == S.top){printf("栈为空\n");return true;}else{printf("栈不为空\n");return false;}}//获取栈顶元素Status GetTop(SqStack S,SElemType e){//若栈不为空if(!StackEmpty(S)){e = *(S.top-1);printf("栈顶元素值为:%d\n",e);}return 0;}//出栈Status Pop(SqStack &S,SElemType e){//判断栈空if(!StackEmpty(S)){e = *--S.top;printf("栈顶元素%d出栈成功\n",e);}return 0;}//遍历--从栈底到栈顶的元素输出Status StackTraverse(SqStack S){printf("遍历开始:\n");for(SElemType *i=S.base;i<S.top;i++){ //从底部开始,到栈顶的前一个停止printf("%d ",*i);}printf("\n");}//置空Status ClearStack(SqStack &S){S.top = S.base; //不能写成S.base = S.top; 位置不能反了printf("置空成功\n");return 0;}//销毁Status DestoryStack(SqStack &S){free(S.base); //销毁连续空间S.base = NULL; //底指针指针赋空S.top = NULL; //栈栈顶指针赋空S.stacksize = 0; //栈最大容量置为0printf("销毁成功");return 0;}int main(){int n,value1,value2;SqStack S;printf("请输入元素个数");scanf("%d",&n);Creat(S,n);printf("栈中元素的个数为%d\n",StackLength(S));Pop(S,value2);GetTop(S,value1);StackTraverse(S);ClearStack(S);StackEmpty(S);DestoryStack(S);return 0;}————————————————版权声明:本文为CSDN博主「李歘歘」的原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接及本声明。原文链接:https://lichuachua.blog.csdn.net/article/details/104524813
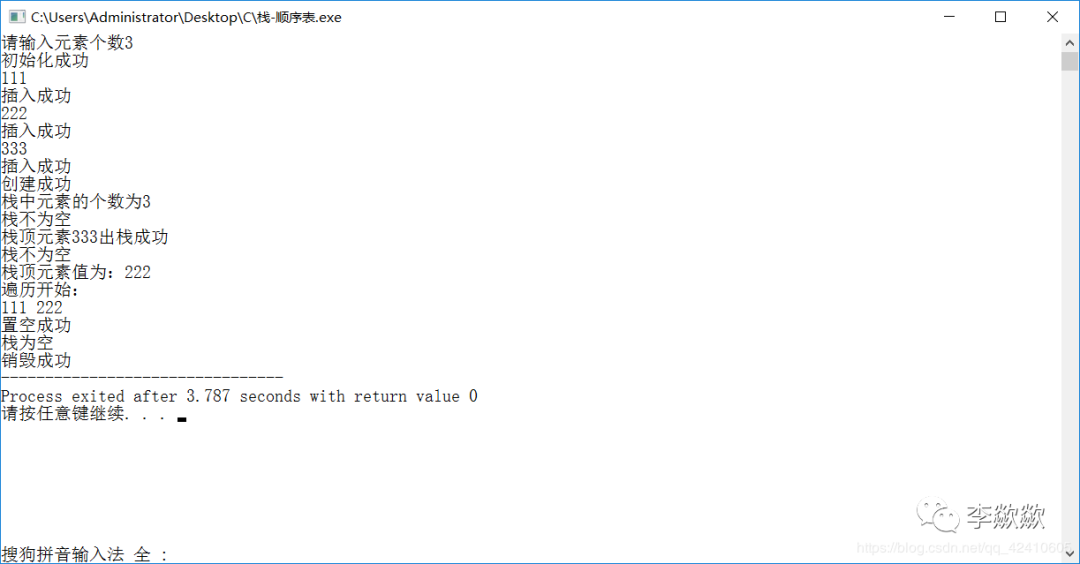
运行结果:
「往 • 期 • 精 • 选」
这些经典排序,你必须掌握
最短路径——Dijkstra算法这一篇就够了

文章转载自编程Cookbook,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。







