关于机器学习-基于2023年度各省统计数据的降维后再Kmean聚类后的另一种可视化

# 导入库
import pandas as pd # panda库
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler # 标准化库
from sklearn.cluster import KMeans  # 导入sklearn聚类模块
from sklearn.metrics import silhouette_score   # 效果评估模块
from sklearn.decomposition import PCA
import matplotlib

# 替换为你的文件路径
data_path = r'E:\JetBrains\PythonProject\DeepLearning\provicedata.csv'
df = pd.read_csv(data_path)
# 选择特征列
features = ['GDP', 'Primary industry', 'Primary industry','Primary industry',
            'resident population','population growth rate',
            'import and export','export value','import value',
            'General budget revenue','General budget expenditure',
            'Per capita disposable income','Per capita consumption expenditure','area']  # 替换为你的特征列名
X = df[features]
n_samples, n_features = X.shape
print('样本数：%d , 特征数：%d' % (n_samples, n_features))

# sklearn.cluster.KMeans(n_clusters=K)
# 1. n_cluster：聚类个数（即K），默认值是8。
# 2. init：初始化类中心的方法（即选择初始中心点的根据），默认“K-means++”，其他可选参数包括“random”。
# 3. n_init：使用不同类中心运行的次数，默认值是10，即算法会初始化10次簇中心，然后返回最好的一次聚类结果。
# 4. max_iter：单次运行KMeans算法的最大迭代次数，默认值是300。
# 5. tol：浮点型，两次迭代之间簇内平方和下降的容忍阈值，默认为0.0001，如果两次迭代之间下降的值小于tol所设定的值，迭代就会停下。
# 6. verbose:是否输出详细信息，参数类型为整型，默认值为0，1表示每隔一段时间打印一次日志信息。
# 7. random_state：控制每次类中心随机初始化的随机种子，作用相当于能够锁定和复现同一次随机结果，默认为none，也可以随机设置数字。
# 8. copy_x：在预先计算距离时，首先将数据居中在数值上更准确。如果 copy_x 为 True(默认)，则不修改原始数据。
#   如果为 False，则修改原始数据，并在函数返回之前放回，但通过减去再添加数据均值可能会引入小的数值差异。
#   请注意，如果原始数据不是C-contiguous，即使copy_x 为False，也会进行复制。如果原始数据是稀疏的，但不是 CSR 格式，即使 copy_x 为 False，也会进行复制。
# 9. algorithm：有三种参数可选：auto”, “full”, “elkan”，默认为auto。K-means 算法使用。
#   经典的EM-style算法是“full”。通过使用三角不等式，“elkan” 变体对具有明确定义的集群的数据更有效。
#   然而，由于分配了一个额外的形状数组(n_samples，n_clusters)，它更加占用内存。

# 数据归一化
scaler = StandardScaler()
scalerX = scaler.fit_transform(X)

for i in range(2,5):
    # 1.components_ ：特征空间中的主轴，表示数据中最大方差的方向。组件按排序 explained_variance_
    # 2.explained_variance_：它代表降维后的各主成分的方差值。方差值越大，则说明越是重要的主成分
    # 3.explained_variance_ratio_：它代表降维后的各主成分的方差值占总方差值的比例，这个比例越大，则越是重要的主成分
    # 4.singular_values_：每个特征的奇异值，奇异值等于n_components 低维空间中变量的2范数
    # 5.mean_：每个特征的均值
    # 6.n_components_：即是上面输入的参数值
    # 7.n_features_：训练数据中的特征数量
    # 8.n_samples_：训练数据中的样本数
    # 9.noise_variance_：等于X协方差矩阵的（min（n_features，n_samples）-n_components）个最小特征值的平均值
    pca = PCA(n_components=i)
    pcaX = pca.fit_transform(scalerX)
    print("For n_components={}, The PCA explained_variance_ratio_ is {}".format(i, pca.explained_variance_ratio_))
    # For n_components=2, The PCA explained_variance_ratio_ is [0.54113074 0.30908829]
    # For n_components=3, The PCA explained_variance_ratio_ is [0.54113074 0.30908829 0.06978044]
    # For n_components=4, The PCA explained_variance_ratio_ is [0.54113074 0.30908829 0.06978044 0.04070103]

pca = PCA(n_components=2)
pcaX = pca.fit_transform(scalerX)

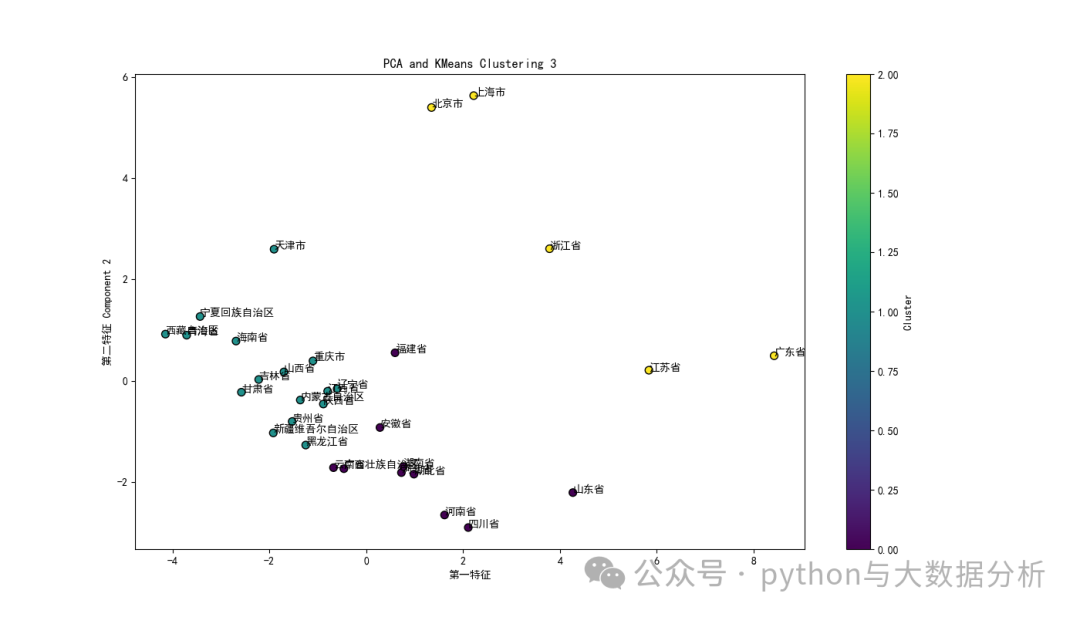
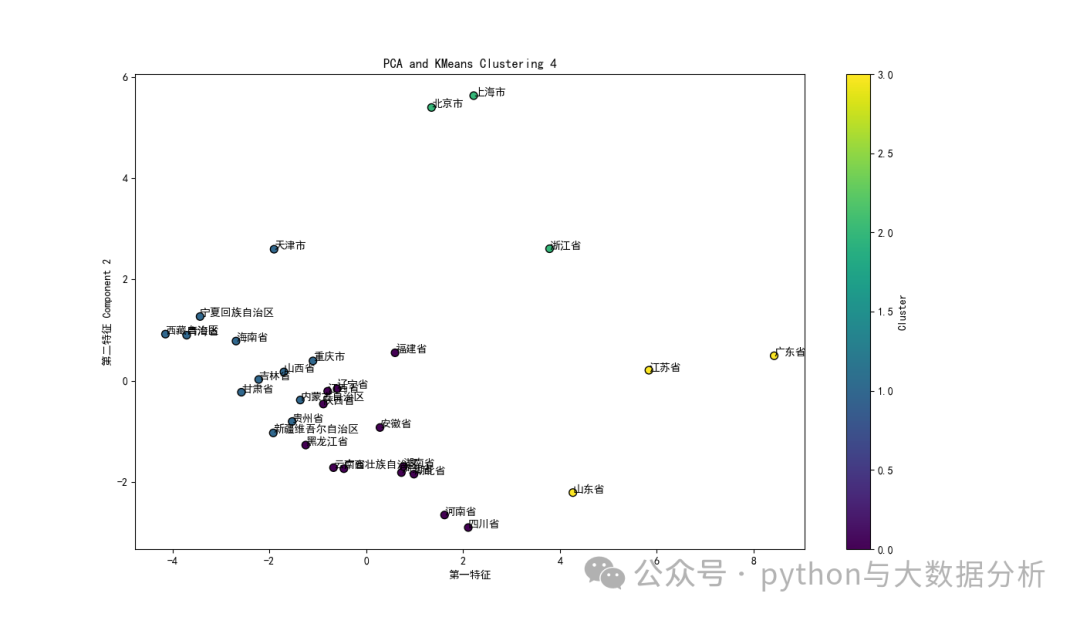
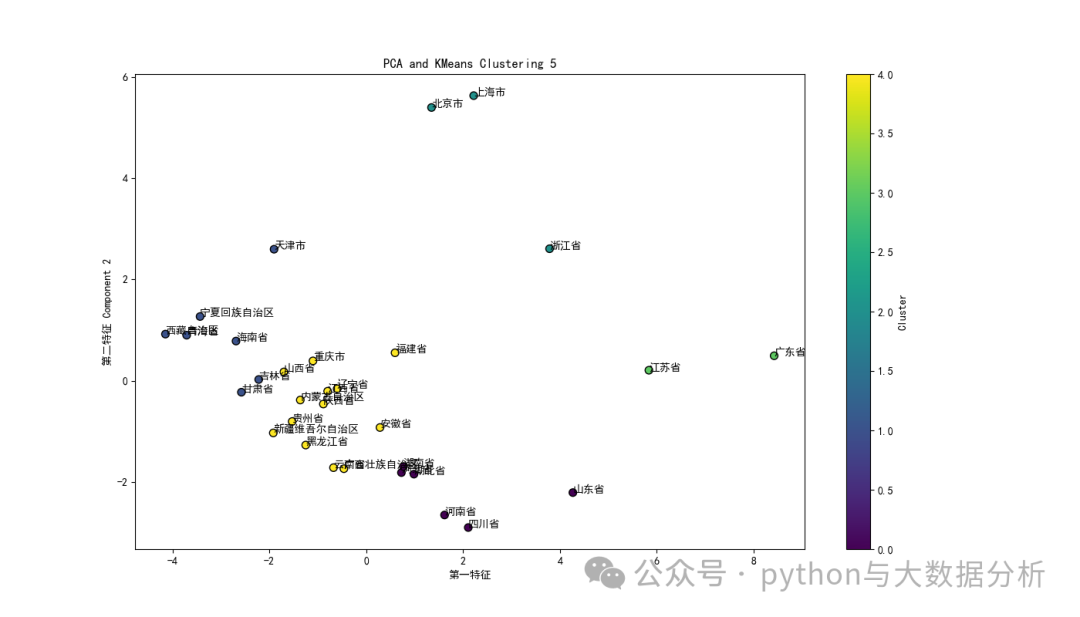
以下代码主要是在不同聚类类别聚类过程中，同时基于PCA的主成分进行特征可视化展示。

# 设置matplotlib正常显示中文和负号
matplotlib.rcParams['font.family'] = 'SimHei'  # 设置字体为黑体
matplotlib.rcParams['axes.unicode_minus'] = False  # 正确显示负号
for k in range(3,6):
    # 模型训练
    KmeansModel = KMeans(n_clusters=k, random_state=42)
    KmeansModel.fit(pcaX)
    kmeansY = KmeansModel.predict(pcaX)
    # 计算轮轴系数：
    # 轮廓系数用于计算每个样本的平均簇内距离a(样本i到同簇其他样本的平均距离，ai值越小说明该样本越应该被聚到该类，即簇内不相似度)和平均邻近簇距离b(样本i到其他相邻簇的所有样本的平均距离bi，bi越大说明样本i越不属于其他簇，即簇间不相似度)。
    # 每个样本的轮廓系数计算公式为：(b-a)/Max(a,b)，轮廓系数越接近1说明结果越好（聚类越准确），越接近-1说明结果越差，若值在0值附近，则说明样本在两个簇的边界上
    score = silhouette_score(pcaX, KmeansModel.labels_, metric='euclidean')
    print("For n_clusters={}, The Silhouette Coefficient is {}".format(k, score))
    # 合并数据和特征
    kmeans_labels = pd.DataFrame(KmeansModel.labels_, columns=['scaler pca kmean labels'+str(k)])
    df = df.join(kmeans_labels)

    # 绘制结果
    plt.figure(figsize=(14, 8))
    plt.scatter(pcaX[:, 0], pcaX[:, 1], c=KmeansModel.labels_, cmap='viridis', marker='o', edgecolor='k', s=50)  # 绘制聚类结果
    for i, txt in enumerate(df['city']):
        plt.text(pcaX[:, 0][i], pcaX[:, 1][i], txt)
    plt.xlabel('第一特征')
    plt.ylabel('第二特征 Component 2')
    plt.title('PCA and KMeans Clustering '+str(k))
    plt.colorbar(label='Cluster')  # 显示颜色条表示不同的聚类中心
    plt.show()

三个聚类簇时的可视化展现效果