DSE精选文章 | 云环境中面向安全动态Skyline查询处理的高效框架

1. 动态Skyline查询

动态Skyline查询（Dynamic Skyline Query，DSQ）是Skyline查询的变体，不仅仅从给定的数据集中计算Skyline点，而且根据查询点q返回一系列不被其他点支配的点，换言之这些点比其它点与q更为相似。

块嵌套循环（Block Nested Loop，BNL）算法（算法1）是一种常见的DSQ算法，基本步骤包括计算数据点与查询q的差值并进行比较，以及逐个检查哪些点可以被或不能被包含在结果集中。

算法1. 用于DSQ的BNL算法

2. 顺序动态加密（ORE）

顺序揭示加密方案（Order-Revealing Encryption schemes，ORE）包括Setup（生成密钥）、Encrypt（加密消息）和Compare（比较密文）三个部分。ORE的特点是允许在保持密文的情况下安全地比较加密的数据，本文在数据集可变的情况下，基于BNL算法和ORE加密实现了安全的DSQ查询。

1. DSQ操作的简化

根据算法1，处理给定查询点q的DSQ需要进行减法和比较两个操作，没有现有的加密方案可以同时支持这两种操作。SCALE框架基于图1揭示的一个简单事实：

（1）当q[j] < p_α[j] < p_β[j]时，t_α[j] - t_β[j] = (p_β[j] - q[j]) - (p_α[j] - q[j]) = p_β[j] - p_α[j];

（2）当p_α[j] < q[j] < p_β[j]时, t_α[j] - t_β[j] = (p_β[j] - q[j]) - (q[j] - p_α[j]) = p_β[j] + p_α[j] - 2q[j];

其中q[j]、p_α[j]和p_β[j]分别代表查询点q、数据点p_α和p_β第j个维度的值，t_α[j]、t_β[j]为数据点与查询点在第j个维度的差值。

也就是说，DSQ的减法和比较操作，可以分解为p_α[j]和p_β[j], p_β[j]+p_α[j]和2q[j]的比较操作，这样便可以使用支持密文比较的加密方案ORE来实现DSQ。

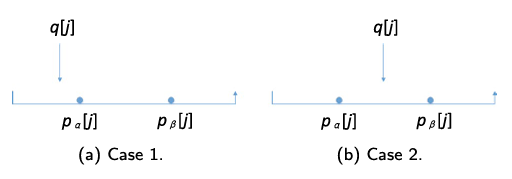
图1. DSQ中q和(p_α, p_β)之间的大小关系

2. 数据库加密

数据库加密阶段，论文讨论了使用ORE实现DSQ时防止泄密和加密管理的两个问题。

2.1 顺序泄密

根据1中的分析，我们将比较操作涉及到的元素分为两种，原数据（如p_α[j],p_β[j]）与数据和（p_β[j]+p_α[j]），对应的两种密文分别记为E(P) 和E(Φ)。ORE对原数据采用相同的密钥加密，此时如果对数据和仍然使用相同的密钥加密，就可能会出现泄密的问题。论文给出的方案是将数据和划分为若干个顺序明显类（Order-Obvious Class，OOC）：在OOC内使用相同的密钥加密，在OOC间使用不同的密钥加密。

对于包含n个元素的配对求和，可以划分为若干个不相交的子集，使得每个子集中的所有求和都是顺序明显的，这样的子集称为OOC。图2给出了一个划分的示例，已知ORE已经暴露了5个数据的大小关系（b<c<a<e<d），通过图示的画线方式，可以将b、c、a、e、d的数据和分为两组，组内的元素大小顺序是很容易推断出来的，而且和已暴露的关系一致，不会引入额外的信息，而组间采用了不同的密钥加密，因此也不会引入额外的信息，这样就实现了在ORE之外不泄露额外信息的情况下最小化所需密钥数。论文还给出了任意维度上OOC个数（即对应密钥数）的理论公式。

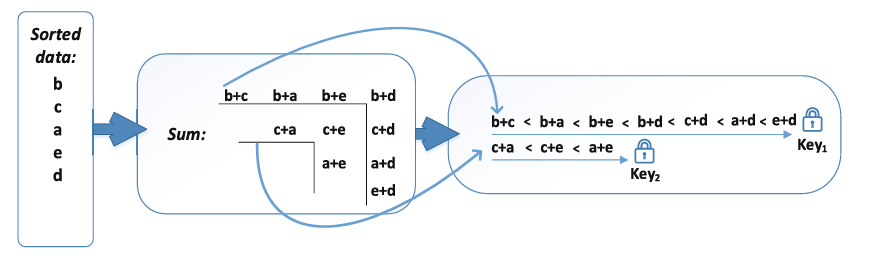
图2. 将数据和划分为多个顺序明显类

2.2 加密管理

为了进一步提升性能，论文还对加密的数据进行了密钥生成、数据和索引、索引检索三方面的优化，密文的存储架构如图3所示。

密钥生成方面，首先存储一个主密钥mk，然后为图2中的每一组OOC分配一个随机的Id_i，组密钥通过mk ⊕ Id_i 生成。

数据和索引方面，建立了从E(P) 到E(Φ)的映射。假设E(P)中p_α[j]、p_β[j]对应密文Enc(p_α[j])、Enc(p_β[j])的索引分别为α和β，那么E(Φ)中p_α[j]+ p_β[j]对应密文Enc(p_α[j]+ p_β[j])的索引可以通过h(α, β)来获取。

索引检索方面，采用基于AVL树的结构来构建索引结构，每棵AVL树的根节点是每个OOC的中位数，AVL树中的所有节点都是同一OOC中和的对的相应密文。

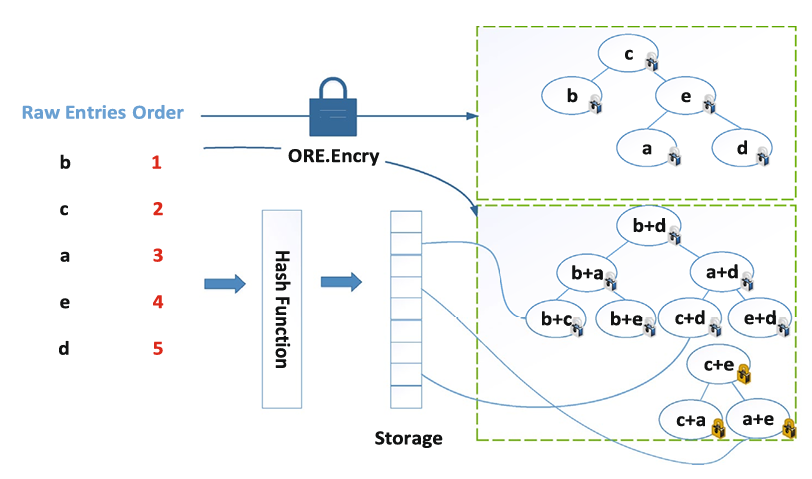
图3. 密文的完整存储架构

3. 查询处理

查询处理的过程如算法2所示，通过对每个维度的查询q[j]、查询倍增和2q[j]、原数据p_α[j], p_α[j]、数据和p_α[j]+p_α[j]进行加密，可以仅用密文的比较操作实现BNL算法，此过程不需要进行解密。

算法2. 加密Skyline查询算法

4. 维护问题

维护问题包括数据库记录的插入、删除和更新，这些操作都围绕AVL树这一数据结构进行。

插入时，首先需要对新插入的记录进行加密，然后求出新的加密数据和，根据数据和在OOC的位置，使用不同的密钥进行加密。每一组OOC都是一棵AVL树，还需要在AVL树中根据大小进行插入操作。图4展示了插入的具体流程。

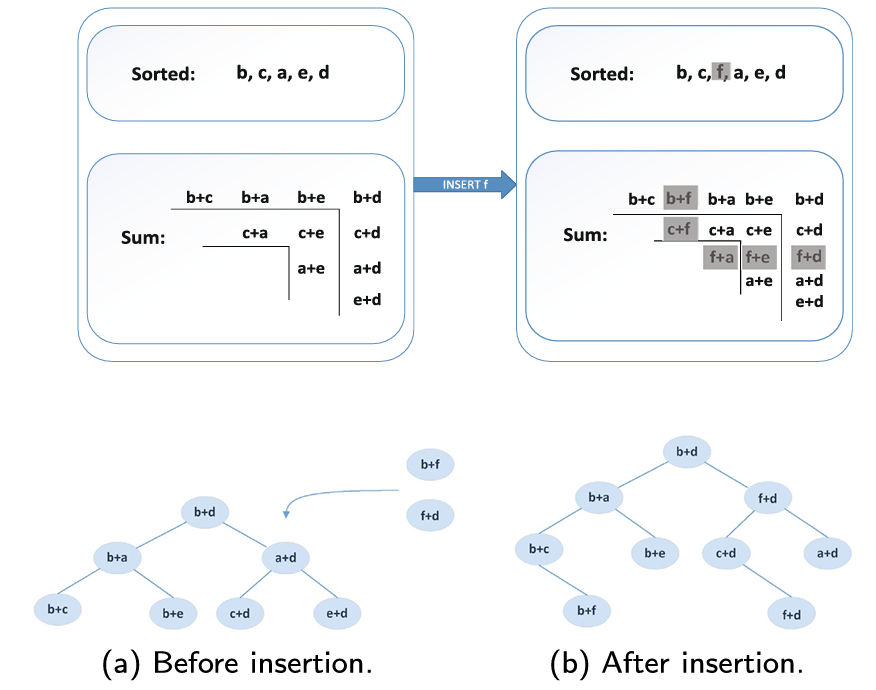
图4. 数据库插入示例

删除的过程和插入类似，在移除被删数据密文的同时，也要移除对应的加密数据和，然后在AVL树中进行删除。

在密文存储架构中不支持更新操作，而是将更新操作视作删除现有的加密记录，然后插入一个新的加密记录。

论文还讨论了SCALE框架的安全性与复杂性，论文证明了该方案是安全的，并且采用AVL树存储索引的情况下，维护操作的复杂度为O (nlogn)。

5. DIST-SCALE

为了缩短并行计算系统中的查询时间，论文提出了两个变体：DIST-SCALE-S和DIST-SCALE-E，适用于主-从节点集群架构。主节点负责数据分配，从节点在其分区内执行SQ操作。处理查询请求分为两个阶段：第一阶段，各从节点运行SCALE算法生成本地SQ结果；第二阶段，主节点合并这些结果为全局SQ结果。

5.1 DIST-SCALE-S

DIST-SCALE-S将数据分区并分配给多个计算节点来实现DSQ查询。

处理过程如图5所示，假设t₁ < t₂ < … < t_v，第一次合并在t₂发生，节点1、2的DSQ结果合并为新的数据集P，类似的合并还在t₄、t₆时进行，结果称为layer-2分区，并立即被发送到空闲的从节点中（如t₁），此时如果另一个从节点也空闲下来（例如t₃），那么就会在这一对从节点中对layer-2分区进行查询，接着主节点将layer-2分区的本地DSQ结果合并为layer-3分区，以此类推，最终合并成一个分区。

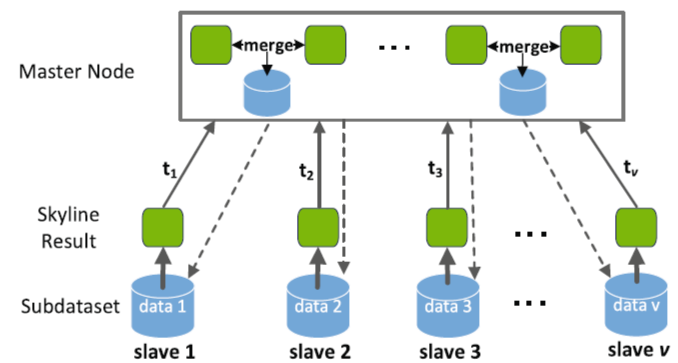
图5. 并行查询处理架构

5.2 DIST-SCALE-E

DIST-SCALE-E在DIST-SCALE-S的基础上进行了改进。主节点在生成上一层结果后不立即分配下一层任务，而是延迟至所有上一层结果生成后再重新分配。此方式避免了多个空闲从节点的出现。

DIST-SCALE-E区分了两种模式并在执行过程中切换：模式2用于“洗牌”，将结果均匀分成v个分区，确保每个从节点获得不同的数据子集；模式1用于解决处理时的无限循环，主节点将所有元组发送给一个空闲的从节点（即只有一个分区）。

模式切换的目的是为了使得分区数量减少，并最终只剩下一个分区。假设在第i层的时候需要切换到模式1，那么相比于第i层使用模式2，到第i+1层才使用模式1，需要处理的分区数量应该满足：|S⁽ⁱ⁾|≤|S⁽ⁱ⁾|/v+|S⁽ⁱ⁺¹⁾|，即|S⁽ⁱ⁾|/|S⁽ⁱ⁺¹⁾|≥1-1/v。

此外，还应考虑最终在第i层切换到模式1时的分区数量不能过大，例如限制|S⁽ⁱ⁾|≤λ，将添加了该限制的SCALE变体称为DIST-SCALE-e。

如图7所示，通过对DIST-SCALE-S、DIST-SCALE-E、DIST-SCALE-e三种并行SCALE框架变体的比较，实验结果表明这些变体显著提高了可扩展性，处理大数据集时具有更小的时间开销。DIST-SCALE-e展现了最佳的整体性能。

此外模式转换阈值的合理性得到了验证，随着层数增大，相邻层分区数量之比|S⁽ⁱ⁾|/|S⁽ⁱ⁺¹⁾|逐渐靠近1-1/v，这证明该理论是合理的，但是分区数量λ的设定仍需具体情况具体分析。

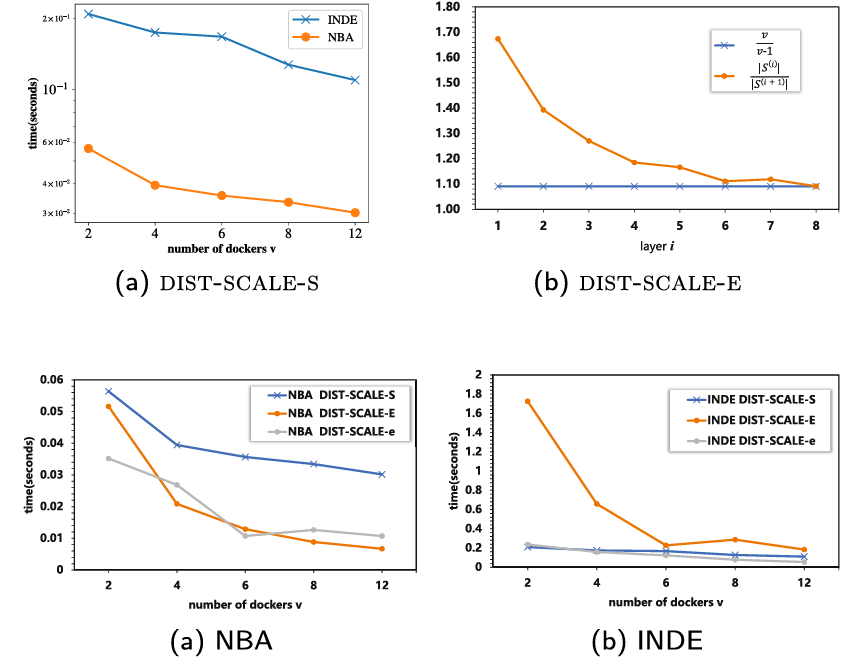
图7. 三种SCALE变体的比较与模式切换的理论分析结果

3. 维护开销

为了证明AVL树作为数据结构的合理性，论文对比了链表、AVL树和红黑树的性能。结果显示链表性能最差，而红黑树和AVL树表现相近，前者在插入和删除效率上略优，但查询性能较低。需要在维护成本和查询性能之间进行权衡。

Data Science and Engineering（DSE）是由中国计算机学会（CCF）主办，数据库专业委员会承办，施普林格·自然（Springer Nature）出版的开放获取（Open Access）期刊。DSE致力于发表与数据科学与工程领域相关的关键科学问题与前沿研究热点，以大数据为研究重点，建设国际学术交流的重要平台，推动学术界和企业界的深度融合。征稿范畴主要包括：数据库系统、大数据管理与分析、大数据治理等相关基础理论、关键技术与系统实践。现任主编（Editors-in-Chief）为数据科学与工程领域的知名专家北京大学崔斌教授和意大利英苏布里亚大学Elena Ferrari教授，现任执行主编(Managing Editor)为数据库专业委员会主任、华东师范大学周傲英教授和浙江大学高云君教授。

目前期刊已被EI、ESCI与SCOPUS收录，2023年CiteScore为10.4，影响因子（Impact factor）为5.1，在计算机科学应用领域排名前12%(92/817)、计算机软件领域排名前12%(49/407)、信息系统领域排名前13%(51/394)，人工智能领域排名前17%(58/350)。稿件处理费由赞助商中新赛克（Sinovatio）承担，欢迎大家免费下载阅读期刊全文，并积极投稿。

原文链接：

https://link.springer.com/article/10.1007/s41019-024-00261-y