数据清洗系统在学术界和工业界广泛应用,但在清洗空间数据方面仍然存在不足。其主要原因在于,现有的先进数据清洗系统主要依靠函数依赖规则,要求有足够的值对共现,以便学习某一属性的值对应另一个属性的值。然而,对于表示位置的空间属性来说,两个记录拥有完全相同的坐标的可能性极低,因此共现几乎不存在。空间数据的清洗系统是有价值且未被解决的难题,本次为大家带来数据库领域顶级会议VLDB 2024的文章《SPARCLE: Boosting the Accuracy of Data Cleaning Systems through Spatial Awareness》。

一. 背景
由于真实数据集的不完美,人们一直致力于开发各种自动数据清理的方法和系统。绝大多数此类方法和方法都是基于规则的,其中各种属性之间的函数依赖关系指导数据的清理过程。但在尝试清理具有空间属性依赖性的数据时却表现不佳(如对于纽约市机动车碰撞数据错误,HoloClean[1]系统仅修复了空间数据58.7%的错误,与它以超过95%的准确度清理非空间数据的能力相比,这是一个相当低的准确度)。作为基于规则的数据清理系统的代表,HoloClean性能差的主要原因有两个:(1)基于函数依赖的清洗系统依赖于值对的充分共现性。然而对于空间属性,由于位置检测设备固有的不准确性,两个记录具有完全相同的坐标的可能性很小。因此,基于规则的系统将无法找到足够的空间共现来用于检测和修复错误条目。(2)在传统的数据清洗系统中,某条记录是否满足规则的结果是二元的(True或False)。然而,在空间规则中,这样的结果需要是模糊的。
作者针对以上的问题,提出了Sparcle(SPatially-AwaReCLEaning)框架,这是一种通过两个主要概念(即空间邻域和距离加权)将空间意识注入基于规则的数据清洗系统核心引擎的创新方法。
二. 体系结构
图1展示了Sparcle架构,其部署在主清洗系统内部。Sparcle接收两种类型的输入:待清洗的原始数据和定义函数依赖关系的约束条件。Sparcle的输出是检测到的错误单元格,其中单元格指的是某一记录的某一属性,同时还包含每个单元格的建议正确值的加权列表。在内部,Sparcle遵循与基于规则的数据清洗系统类似的架构,主要由三个模块组成:空间错误检测器、空间候选生成器和空间输入公式化器。
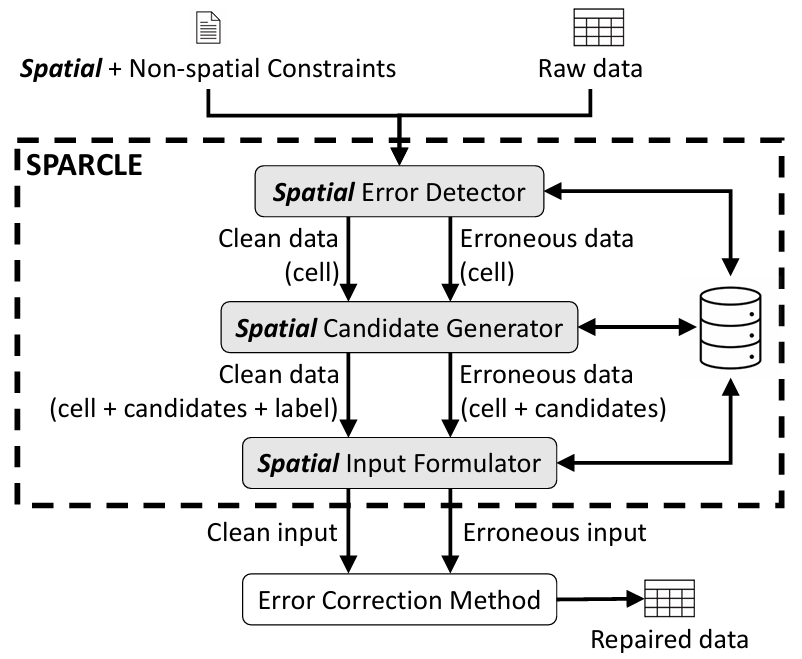
图1 Sparcle架构
三. 空间错误检测器
Sparcle扩展了约束语言以支持空间否定约束。这只是语言上的扩展,而不是新增一种约束类别。这使得Sparcle能够继承否定约束的所有系统支持功能,包括约束满足、验证和推导。Sparcle支持以下Spatial Range(空间范围)否定约束构造:
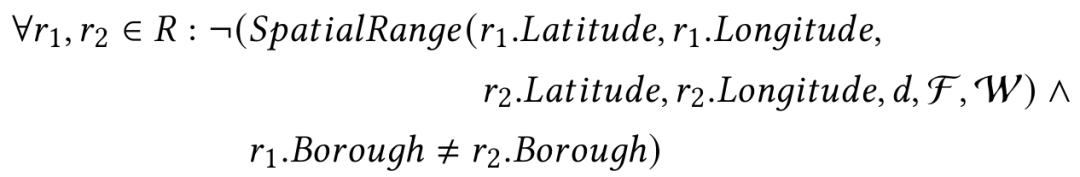
这表明,如果两个记录r1和r2根据距离函数F的计算结果在距离范围d内,那么根据权重函数W,它们可能属于相同的行政区(borough)。距离函数F负责实现空间邻域的概念,可以采用欧几里德距离或道路网络距离。权重函数W(r1, r2)负责实现距离加权的概念,使用任意函数(例如线性或指数函数),根据r1和r2之间的距离从0增加到d,返回从1到0的递减值。当F(r1, r2) < d时,Spatial Range返回一个非零值(基于W),否则,返回False。Sparcle还支持具有kNN否定约束,其语言结构如下:
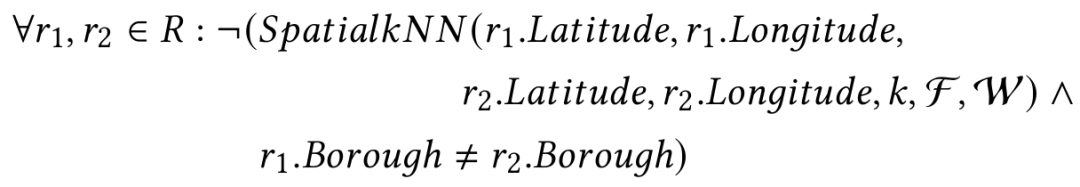
这表示,如果记录r2是记录r1根据距离函数F计算出的k个最近记录之一,则根据权重函数W,它们可能属于相同的行政区。当r2是r1的k个最近记录之一时,Spatial kNN返回一个非零值(基于W的计算结果);否则,返回False。
Sparcle中最需要的操作是空间范围查询和kNN查询,这些操作与底层的空间约束相关。由于这些操作相较于相等性搜索来说是相当昂贵的。Sparcle:(a)采用了空间数据库系统(PostGIS),其中输入的原始数据根据其纬度和经度坐标进行了空间索引;(b)对于每个空间约束C,Sparcle利用空间索引高效地执行基于范围查询或k最近邻查询的自连接操作,查询参数由约束C定义。连接的结果随后被存储在距离矩阵(DistanceMatrix)的表中,该表的模式为:(R1, R2, v1, v2, D, w),其中:
R1和R2是两个记录标识符,使得R2要么位于距离R1的距离d以内,要么是R1的k个最近邻之一。v1和v2是在空间约束C中提到的属性上的对应值,这些属性是需要清洗的。D是根据函数F计算的R1和R2之间的距离,w是根据权重函数W计算的R1和R2之间的距离权重。
图2给出了距离矩阵计算的示例,图2a展示了七个记录的集合,这些记录位于部分地图上,包括来自纽约市两个行政区(曼哈顿和皇后区)的区域,分别用浅蓝色和绿色表示(值得说明的是,数据清理系统并不知道行政区划的边界)。
图2b给出了整个数据集的统计信息,按每个行政区的记录数量划分。这些统计信息由该模块收集,后续模块将在计算中使用这些数据。
图2c给出了图2a中七个记录(r1到r7)的DistanceMatrix,基于一个空间范围否定约束,距离为d = 1km(以红色虚线表示记录之间的距离),以及一个权重函数W,其公式如下:
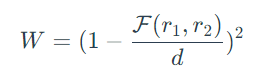
其中F(r1, r2)是R1和R2之间的距离。对于r1,其行政区值为“斯塔滕岛”,有五个记录(从r2到r6)位于距离d以内。因此,在DistanceMatrix中有五个对应的记录。其中,r2和r3的行政区值为“曼哈顿”,距离分别为200米和500米,对应的权重值分别为0.64和0.25。以类似的方式,r2、r3、r4、r5、r6和r7也会在DistanceMatrix中有相应的记录。对于图2中的示例,记录r1到r6的所有行政区单元格将被加入到错误单元格的集合中,因为它们出现在DistanceMatrix的前五行,其中v1 ≠ v2。而r7.Borough将被认为是一个正确单元格,因为它在DistanceMatrix中的所有行中,都有v1 = v2。
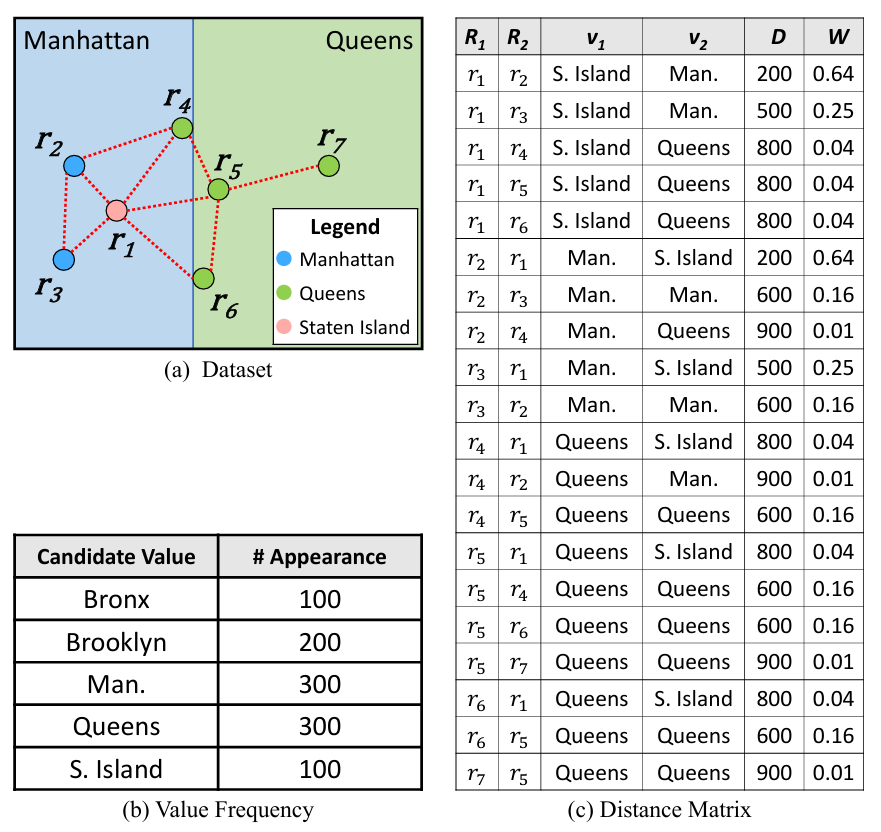
图2 距离矩阵示例
四. 空间候选生成器
对于每个空间约束,空间候选生成器主要分别对其错误单元格列表进行操作,目标是:(1)为每个错误单元格生成候选值列表,以及每个候选值正确的概率,(2)利用生成的候选值概率来决定是否可以将错误单元格移动到正确单元格列表中。这个过程经历三个阶段。第一阶段生成每个错误单元格的初始候选值列表。第二阶段估算每个候选值的正确性概率。第三阶段寻找是否存在一个明确的主导候选值。如果有,则将其视为该单元格的正确值,并将该单元格移至正确单元格列表。
阶段一:ri.Borough的候选值将包括ri.Borough本身,以及根据空间否定约束位于ri附近(范围或kNN)内的任何记录rj的所有Borough值。共现计数从传统的绝对计数放宽为基于共现记录彼此距离多远的加权计数。这通过计算所有同时出现的记录的DistanceMatrix中的权重总和来完成。表1的第二列和第三列给出了候选值列表,以及图2中记录r1的Borough属性的权重总和。对于ri.Borough共有三个候选值:曼哈顿、皇后区和斯塔滕岛。曼哈顿和皇后区的权重分别设置为0.89和0.12,即距离矩阵中相应记录的权重总和,斯塔滕岛的权重设置为默认最小值0.01。
阶段二:形式上,在Sparcle中,记录R的单元格C的候选值v的概率估计为:
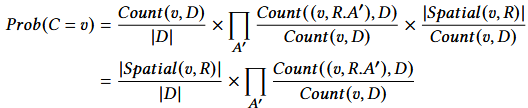
其中,|spatial(v, R)|是是表1的第三列,在第1阶段中计算,Count(v, D)直接从图2b中计算得到的值频率表中获得,对于Count((v, R.A′), D),如果候选值v是原始值则被设置为1,如果非原始值则被设置为0.1,其计算示例如表1所示。
阶段三:Sparcle首先将候选概率归一化,使其总和为1。然后,Sparcle使用两个参数,MinProb和MaxProb。任何概率小于MinProb的候选值将被视为边际值,被移除,并且不再进一步考虑。接着,如果只剩下一个候选值,或者某个候选值的概率明显高于MaxProb,则认为该值是正确值,并将对应的单元格从错误列表移动到正确列表。表2的最后一列给出了归一化概率。假设MinProb = 0.1,则将排除r1的候选值斯塔滕岛。假设MaxProb = 0.9,则不会将r1.Borough任何候选者标记为正确。含有剩余候选值的正确单元格和错误单元格将传递到下一个模块。
表1 r1.Borough的候选生成状态

五. 空间输入制定器
Sparcle在三个数据清理系统的输入公式模块中注入空间邻域和距离加权概念,即AimNet[2]、Baran[3]和HoloClean/MLNClean[1]。
AimNet[52]即HoloClean开源版本的错误修正方法,需要为每个单元格和每个约束构建一个特征向量V,其中v[i]表示该单元格的第i个候选单元违反否定约束的得分。Sparcle不再简单地计数违反约束的次数,而是将违反约束的权重相加。
Baran要求输入为每个单元格的每个候选值的特征向量,每个向量值代表候选值根据特定依赖关系的概率。Sparcle通过使用空间邻近性和候选值的权重来计算综合依赖(如(Latitude, Longitude)→Borough)的概率,从而注入空间感知能力。
HoloClean和MLNClean基于马尔可夫逻辑网络,要求输入以因子图的形式表示。Sparcle通过修改因子图的构建方式,Sparcle通过将因子函数的输出(1或-1)与在图2的DistanceMatrix中计算出的实例权重相乘,来修改因子图的构建。
以上的计算示例如图3所示。
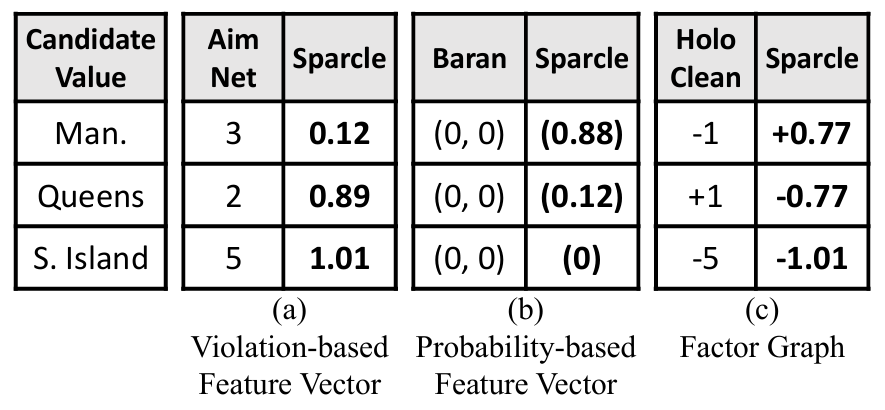
图3 原始方法与Sparcle输入的r1.Borough对比
六. 实验结果
数据集:实验使用了四个真实数据集(Austin-Code、Boston-311、Chicago-Building、NYC-Crash)和一个合成数据集(Chicago-Synthetic)。这些数据集涵盖了不同的空间依赖关系,如邮政编码、城市、行政区划等。
评估指标:使用精确度、召回率和F1分数来评估数据清洗的准确性,同时记录系统的运行时间以评估效率。
比较对象:Sparcle与现有的数据清洗系统(如HoloClean、Baran)以及一种基于矩阵分解的空间数据清洗方法(SMFL)进行比较。
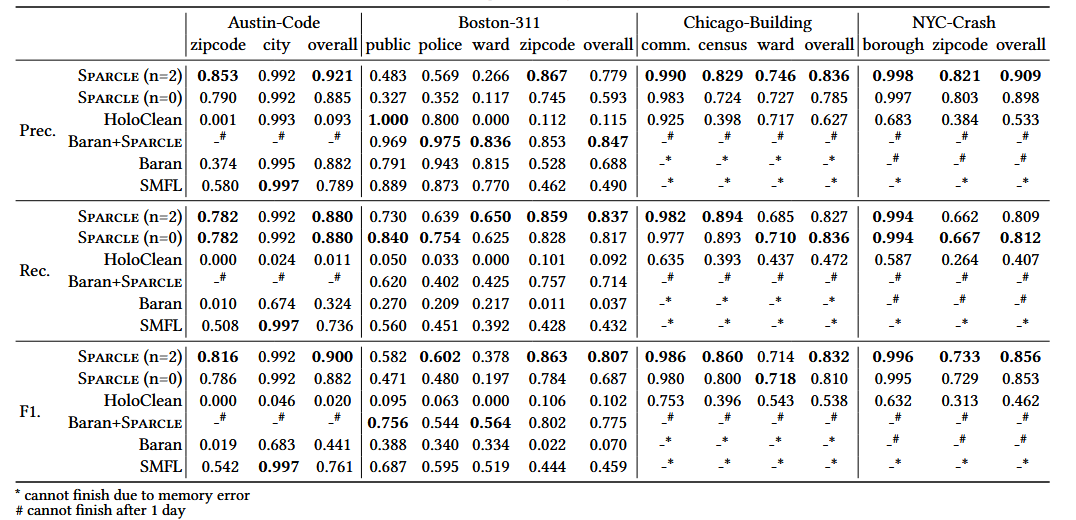
准确性提升:
与HoloClean比较:Sparcle在所有数据集上均显著提高了F1分数,尤其是在召回率方面表现突出。
与Baran比较:Baran+Sparcle在Boston311数据集上将F1分数从0.07提高到0.78,显示出在空间数据上的显著改进。
与SMFL比较:尽管SMFL在某些情况下表现优于HoloClean和Baran,但其准确性仍低于Sparcle和Baran+Sparcle。
表2 真实数据的清理准确性
参数调优:空间范围和最近邻参数:实验表明,较大的空间范围和最近邻参数可以提高准确性,但过大的参数会导致效率下降。建议的参数范围是空间范围不超过2000米,最近邻参数不超过数据集大小与属性值数量的比值。
距离权重因子(距离函数W的参数):使用距离权重因子(如n = 2)可以进一步提高在较小数据集上的准确性,而在密集数据集上影响较小。
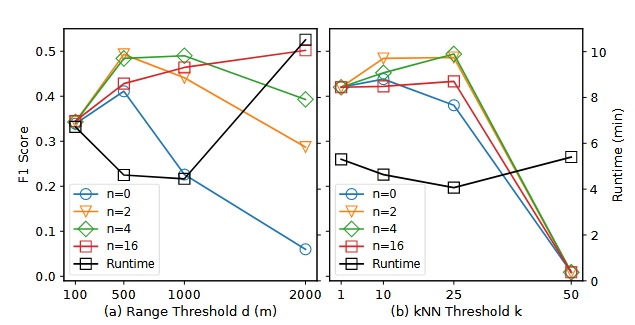
图4 Spacle参数调优
效率:Sparcle在所有数据集上的运行时间比HoloClean增加了17%到29%,主要由于构建距离矩阵的开销。尽管如此,考虑到空间操作的复杂性,这一开销是可以接受的。
七. 总结
论文介绍了新颖的空间数据清理系统Sparcle,该系统的两个主要概念将空间意识注入基于规则的数据清洗系统核心引擎:(1)空间邻域,在此,依赖关系的共现被放宽为在一定空间邻近范围内,而不是要求完全相同的值;(2)距离加权,其中记录根据相对距离的不同,被赋予不同的权重,以决定它们是否满足依赖规则。在最先进的数据清理系统中实际部署 Sparcle ,以及在真实和合成数据集的实验结果表明,Sparcle 在处理空间数据时显着提高了数据清理系统的准确性。
八. 引用
[1] Theodoros Rekatsinas, Xu Chu, Ihab F. Ilyas, and Christopher Ré. 2017. HoloClean: Holistic Data Repairs with Probabilistic Inference. Proceedings of the International Conference on Very Large Data Bases, PVLDB 10, 11 (2017), 11901201.
[2] Richard Wu, Aoqian Zhang, Ihab F. Ilyas, and Theodoros Rekatsinas. 2020. Attention-based Learning for Missing Data Imputation in HoloClean. In Proceedings of Machine Learning and Systems, MLSys (Austin, TX, USA).
[3] Mohammad Mahdavi and Ziawasch Abedjan. 2020. Baran: Effective Error Correction via a Unified Context Representation and Transfer Learning. Proceedings of the International Conference on Very Large Data Bases, PVLDB 13, 11 (2020), 1948–1961.
 |
重庆大学时空实验室(Spatio-Temporal Art Lab,简称Start Lab),旨在发挥企业和高校的优势,深入探索时空数据收集、存储、管理、挖掘、可视化相关技术,并积极推进学术成果在产业界的落地!年度有3~5名研究生名额,欢迎计算机、GIS等相关专业的学生报考!

图文|苏赛男
校稿|孙杨洋
编辑|朱明辉
审核|李瑞远
审核|杨广超






