点击上方“IT那活儿”公众号--专注于企业全栈运维技术分享，不管IT什么活儿，干就完了！！！

KNN算法的核心思想是在一个含未知样本的空间，可以根据样本最近的k个样本的数据类型来确定未知样本的数据类型。

1.1 该算法涉及的3个主要因素

• k值选择；

• 距离度量；

• 分类决策。

1.2 具体流程如下

根据给定的距离度量，在训练集T中找出与x最邻近的 k个点，涵盖这 k 个点的邻域记作 ；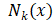

在 中根据分类决策规则(如多数表决)决定 x 的类别 y；

在上式中，I为指示函数，即当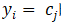时为1，否则为0。

2.1 kNN优点

• 理论成熟，思想简单，既可以用来做分类又可以做回归；

• KNN是一种在线技术，新数据可以直接加入数据集而不必进行重新训练；

• 可用于非线性分类(数据集不要求线性可分)；

• 和朴素贝叶斯之类的算法比，对数据没有假设，准确度高，对异常点不敏感。

2.2 kNN缺点

• 计算量大，尤其是数据集非常大的时候；

• 样本不平衡的时候，对稀有类别的预测准确率低；

• KD树，球树模型建立需要大量的内存；

• k值大小的选择很重要。

如果选择较小的K值，就相当于用较小的领域中的训练实例进行预测，“学习”近似误差会减小，只有与输入实例较近或相似的训练实例才会对预测结果起作用，与此同时带来的问题是“学习”的估计误差会增大。

换句话说，K值的减小就意味着整体模型变得复杂，容易发生过拟合，如果选择较大的K值，就相当于用较大领域中的训练实例进行预测：

其优点是可以减少学习的估计误差，但缺点是学习的近似误差会增大。

这时候，与输入实例较远(不相似的)训练实例也会对预测器作用，使预测发生错误，且K值的增大就意味着整体的模型变得简单，

K=N，则完全不足取，因为此时无论输入实例是什么，都只是简单的预测它属于在训练实例中最多的累模型过于简单，忽略了训练实例中大量有用信息。在实际应用中，K值一般取一个比较小的数值，例如采用交叉验证法(简单来说，就是一部分样本做训练集，一部分做测试集)来选择最优的K值。

kd树是一种对k维空间中的实例点进行存储，以便对其进行快速检索的树形数据结构。kd树是二叉树，表示对k维空间的一个划分。

构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间切分，构成一系列的k维超矩形区域。kd树的每个节点对应于一个k维超矩形区域。

4.1 构造平衡kd树过程

输入：k维空间数据集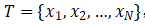，其中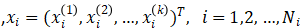

输出：kd树。

• 开始:构造根节点，根节点对应于包含T的k维空间的超矩形区域。

  选择为坐标轴，以T中所有实例的坐标的中位数为切分点，将根节点对应的超矩形区域目分为两个子区域。切分由通过切分点并与坐标轴垂直的超平面实现。

  由根节点生成深度为1的左、右子节点:左子节点对应坐标小于切分点的子区域，右子节点对应于坐标大于切分点的子区域。

  将落在切分超平面上的实例点保存在根节点。

• 重复:对深度为j的节点，选择为切分的坐标轴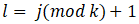，，以该节点的区域中所有实例的坐标的中位数为切分点，将该节点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴垂直的超平面实现。

  由该节点生成深度为j+1的左、右子节点:左子节点对应坐标小于切分点的子区域，右子节点对应坐标大于切分点的子区域。

  将落在切分超平面上的实例点保存在根节点。

• 直到两个子区域没有实例存在时停止，从而形成kd树的区域划分。

4.2 算法:用kd树的最近邻搜索

输入：已构造的kd树:目标点x;

输出：x的最近邻。

• 在kd树中找出包含目标点x的叶节点:从根节点出发，递归地向下访问kd树。若目标点x当前维的坐标小于切分点的坐标，则移动到左子节点，否则移动到右子节点。直到子节点为叶节点为止。

• 以此叶节点为“当前最近点”。

• 递归地向上回退，在每个节点进行以下操作：

  如果该节点保存的实例点比当前最近点距离目标点更近，则以该实例点作为“当前最近点”；

  当前最近点一定存在于该节点一个子节点对应的区域。检查该子节点的父节点的另一子节点(兄弟节点)对应区域是否有更近的点。具体地，检查另一子节点对应的区域是否与以目标点为球心以目标点与“当前最近点”间的距离为半径的超球体相交。

  如果相交，可能在另一个子节点对应的区域内存在距目标点更近的点，移动到另一个子节点。接着递归地进行最近邻搜索;

  如果不相交，向上回退。

• 当回退到根节点时，搜索结束。最后的“当前最近点”即为x的最近邻点。

  如果实例点是随机分布的，kd树搜索的平均计算复杂度是 ，这里 N 是训练实例数。kd树更适用与训练实例数远大于空间维数时的k近邻搜索。当空间维数接近训练实例数时，效率会迅速下降，几乎接近线性扫描。

END