GoGraph：基于更新邻居状态快速迭代的图计算算法

在大数据时代，图计算已成为数据分析的关键技术。然而，传统图计算方法在处理大规模数据时效率低下。文章提出的GoGraph算法，通过优化顶点处理顺序，有效减少迭代轮数，显著提升计算效率。该算法适用于多种图分析任务，如PageRank和SSSP等，为图计算领域提供了新的优化思路。

1.1大数据时代的需求

在当今的大数据时代，随着互联网技术的飞速发展和数据量的爆炸式增长，数据处理和分析的需求日益复杂。传统的集中式数据库系统由于其硬件资源的限制，已经无法满足大规模数据处理的需求。分布式数据库系统应运而生，通过将数据水平分割并分布在多个节点上，实现了系统的可扩展性和高可用性。这种分布式架构使得数据处理能够在多个计算节点上并行执行，从而能够处理更大规模的数据集。

然而，分布式数据库系统也带来了新的挑战，特别是在事务处理方面。分布式事务需要在多个节点之间进行通信和协调，以确保数据的一致性和完整性。这种多节点通信导致了较高的网络开销和复杂的事务管理机制，从而影响了系统的性能和效率。

1.2分布式事务处理的挑战

分布式事务处理的核心挑战在于如何在多个节点之间高效地协调和管理事务。传统的事务处理方法在分布式环境下面临以下主要问题：

• 多节点通信开销：分布式事务需要在多个节点之间进行数据传输和状态同步，这导致了较高的网络延迟和带宽消耗。

• 数据一致性维护：在分布式环境下，确保数据在多个节点之间的一致性变得非常困难。事务的原子性、一致性、隔离性和持久性（ACID）需要在多个节点上协同实现。

• 故障恢复复杂性：分布式系统中节点故障的概率更高，事务处理需要考虑故障恢复机制，增加了系统的复杂性。

这些问题使得分布式事务处理的性能和效率成为制约大规模数据应用发展的关键因素。

1.3迭代计算的优化需求

在图计算等场景中，迭代计算是一种重要的方法，用于解决诸如PageRank、单源最短路径（SSSP）、广度优先搜索（BFS）等问题。迭代计算通常需要多次遍历整个图，更新顶点状态，直到达到收敛条件。这种计算模式虽然在理论上具有很强的解决问题能力，但在实际应用中却面临着效率低下的问题。

现有的优化方法主要集中在减少每次迭代的运行时间，例如通过优化算法实现、利用硬件加速等手段。然而，这些方法往往忽略了减少迭代轮数的重要性。实际上，迭代轮数的多少直接影响到计算的总时间，特别是在大规模图数据上，减少迭代轮数可以显著提高计算效率。

1.4现有方法的不足

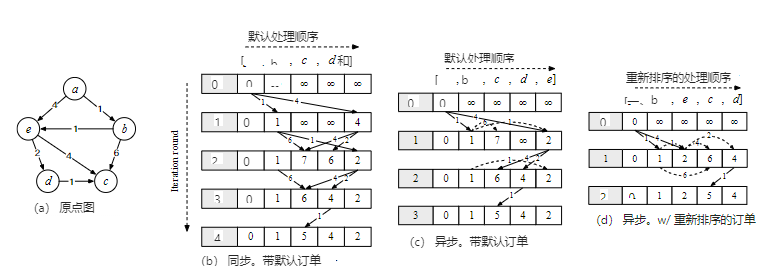
传统的迭代算法通常采用同步模式进行计算，即在每一轮迭代中，所有顶点基于前一轮的状态进行更新。这种模式虽然简化了并行语义，但存在以下不足：

• 迭代轮数固定：在同步模式下，达到特定收敛状态所需的迭代轮数通常被认为是固定的，无法通过调整计算方式来减少。

• 无法利用最新状态：顶点更新时只能使用前一轮的状态，无法利用当前轮次中其他顶点的最新状态，导致收敛速度较慢。

一些研究探索了异步计算模式，允许顶点在迭代过程中使用当前轮次的最新状态。然而，这些方法通常需要用户定义的顶点选择策略，增加了使用难度，并且在实际应用中可能引入不稳定性。

为应对上述挑战，文章提出了一种图重排序方法GoGraph。该方法通过构建有效的顶点处理顺序，减少迭代轮数，加速迭代计算。GoGraph的核心在于优化顶点处理顺序，使更多顶点能在同一迭代中利用邻居的最新状态，从而加快收敛速度。

GoGraph的创新之处在于将顶点重排序问题转化为最大化正向边数量的问题，并通过分治策略高效求解。这种方法不仅考虑了图的结构特性，还兼顾了计算过程中的实际需求，如内存访问效率等。

2.1提出GoGraph

为应对上述挑战，文章提出了一种图重排序方法GoGraph。该方法通过构建有效的顶点处理顺序，减少迭代轮数，加速迭代计算。GoGraph的核心在于优化顶点处理顺序，使更多顶点能在同一迭代中利用邻居的最新状态，从而加快收敛速度。

GoGraph的创新之处在于将顶点重排序问题转化为最大化正向边数量的问题，并通过分治策略高效求解。这种方法不仅考虑了图的结构特性，还兼顾了计算过程中的实际需求，如内存访问效率等。

2.2GoGraph算法概述

GoGraph是一种图重排序方法，旨在通过优化顶点处理顺序来减少迭代轮数，从而加速迭代计算。其核心思想是通过调整顶点的处理顺序，使得在迭代过程中，更多的顶点能够利用其邻居的最新状态，从而加快收敛速度。

2.2.1度量函数

为了量化顶点处理顺序在加速迭代计算方面的效率，GoGraph引入了一个度量函数M(OV)。该函数通过计算源顶点在目的顶点之前的边数来反映处理顺序的质量。具体来说，M(OV)计算所有边中源顶点序号小于目的顶点序号的边的数量。通过最大化M(OV)，GoGraph确保更多顶点能在迭代中利用邻居的最新状态，从而加快收敛速度。

2.2.2分治策略

GoGraph采用分治策略进行顶点重排序，具体步骤如下：

1. 提取高阶顶点和孤立顶点：识别并移除图中的高阶顶点和孤立顶点，以简化后续处理。

2. 划分剩余顶点：将剩余图划分为较小的子图，以降低重排序的复杂度。

3. 在子图内重排序顶点：对每个子图内的顶点进行重排序，优先选择与当前处理顺序中顶点局部性更好的顶点插入到处理顺序中。

4. 重排序子图：将子图视为超级顶点，根据子图间的边权重重新排序，以优化全局处理顺序。

5. 插入高阶和孤立顶点：将之前移除的高阶顶点和孤立顶点插入到最终的处理顺序中，完成整个顶点重排序过程。

2.3GoGraph算法的详细步骤

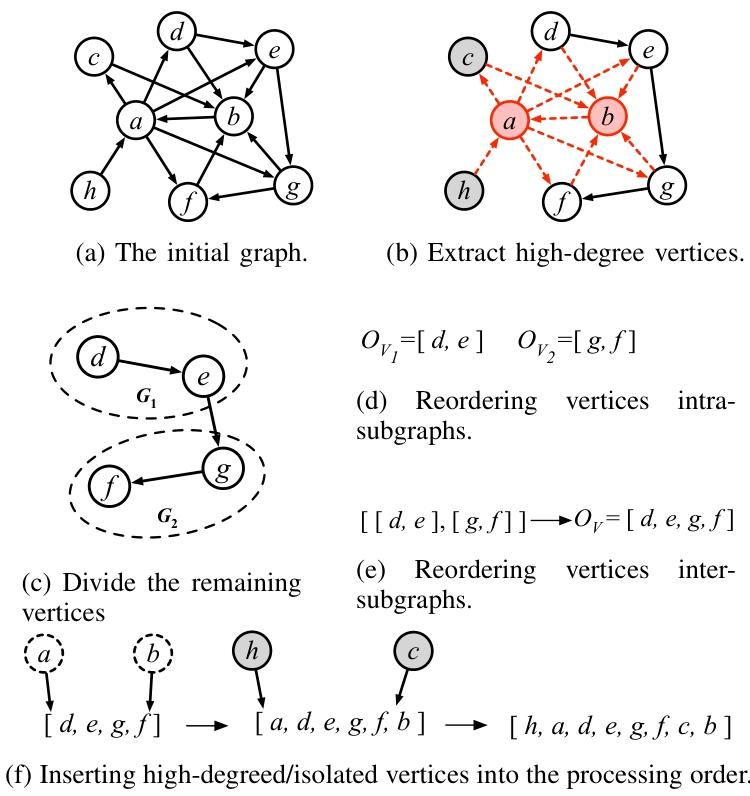
GoGraph的说明性示例

2.3.1提取高阶顶点和孤立顶点

在图中，高阶顶点（即度数非常高的顶点）对低阶顶点的定位决策有显著影响。因此，GoGraph首先识别并移除这些高阶顶点，以简化后续的重排序过程。同时，孤立顶点（即没有边连接的顶点）也会被移除，因为它们对整个图的连通性没有贡献。

2.3.2划分剩余顶点

将剩余的顶点划分为较小的子图，可以降低重排序的复杂度。在划分过程中，GoGraph确保子图内部的边数尽可能多，而子图之间的边数尽可能少。这样可以保持顶点的局部性，减少全局重排序的复杂性。

2.3.3在子图内重排序顶点

对于每个子图，GoGraph采用贪心算法进行顶点重排序。具体来说，算法会随机选择一个初始顶点，然后逐步插入其他顶点到最优位置，以最大化度量函数M(OV)的值。在插入过程中，会优先选择与当前处理顺序中顶点局部性更好的顶点。

2.3.4重排序子图

将子图视为超级顶点后，GoGraph根据子图间的边权重重新排序这些超级顶点。子图间的边权重定义为两个子图之间边的数量。通过这种方式，GoGraph可以优化全局处理顺序，使得在迭代过程中，更多的顶点能够利用其邻居的最新状态。

2.3.5插入高阶和孤立顶点

最后，GoGraph将之前移除的高阶顶点和孤立顶点插入到最终的处理顺序中。在插入过程中，会寻找最优的位置，以最大化度量函数M(OV)的值。

2.4GoGraph算法的实现细节

2.4.1初始化

在实现过程中，首先初始化每个顶点的val值为无穷大，val值用于表示顶点在处理顺序中的序号。然后，提取高阶顶点和孤立顶点，并将剩余的顶点划分为多个子图。

2.4.2子图内重排序

对于每个子图，GoGraph通过贪心算法进行顶点重排序。具体来说，算法会随机选择一个初始顶点，然后逐步插入其他顶点到最优位置。在插入过程中，会计算插入每个顶点后的度量函数M(OV)的值，并选择使M(OV)最大的位置进行插入。

2.4.3子图间重排序

将子图视为超级顶点后，GoGraph根据子图间的边权重重新排序这些超级顶点。子图间的边权重定义为两个子图之间边的数量。通过这种方式，GoGraph可以优化全局处理顺序，使得在迭代过程中，更多的顶点能够利用其邻居的最新状态。

2.4.4插入高阶和孤立顶点

最后，GoGraph将之前移除的高阶顶点和孤立顶点插入到最终的处理顺序中。在插入过程中，会寻找最优的位置，以最大化度量函数M(OV)的值。

2.5GoGraph算法的优势

2.5.1提高计算效率

通过优化顶点处理顺序，GoGraph能够减少迭代轮数，从而显著提高计算效率。实验结果表明，GoGraph在运行时间和迭代轮数方面均优于其他方法。

2.5.2降低资源消耗

GoGraph通过减少迭代轮数和优化内存访问模式，降低了系统的资源消耗。特别是在大规模分布式环境下，这种优化具有重要的实际意义。

2.5.3兼容性

GoGraph算法可以与现有的图计算框架和硬件加速技术相结合，进一步提升计算性能。它不依赖于特定的硬件架构，具有良好的兼容性和可扩展性。

2.6GoGraph算法的应用场景

2.6.1大规模图数据处理

GoGraph适用于处理大规模图数据，如社交网络、推荐系统、交通网络等。在这些场景中，图的规模通常非常大，传统的图计算方法难以满足性能要求。

2.6.2分布式计算环境

在分布式计算环境中，GoGraph可以通过优化顶点处理顺序，减少节点之间的通信开销，提高系统的并行度和效率。

2.6.3实时图分析

对于需要实时响应的图分析任务，如欺诈检测、网络安全监控等，GoGraph能够通过减少迭代轮数，加快计算速度，满足实时性要求。

3.1实验背景与目标

在大数据时代，图计算已经成为数据分析的重要工具。然而，传统的图计算方法在处理大规模图数据时面临着效率低下的问题。特别是在迭代计算中，如何减少迭代轮数，提高计算效率，成为一个关键的研究方向。GoGraph算法正是为了解决这一问题而提出的。

本实验旨在评估GoGraph算法在不同图数据集和图分析算法上的性能表现，验证其在减少迭代轮数和提高计算效率方面的有效性。通过与多种现有的图重排序方法进行对比，展示GoGraph的优势和适用性。

3.2实验设置

3.2.1硬件环境

实验在一台Linux服务器上进行，服务器配置如下：

• CPU：Intel Xeon Gold 6248R 3.00GHz

• 内存：98GB

• 操作系统：64位Ubuntu 22.04

• 编译器：GCC 7.5

3.2.2图工作负载

实验使用了四种典型的图分析算法：

3.2.3数据集

实验使用了六个真实世界的数据集，具体信息如下：

• Indochina：11,358个顶点，49,138条边

• SK-2005：121,422个顶点，367,579条边

• Google：875,713个顶点，5,241,298条边

• Wikipedia-2009：1,864,433个顶点，4,652,358条边

• Cit-Patents：3,774,768个顶点，18,204,371条边

• LiveJournal：4,033,137个顶点，27,972,078条边

3.2.4竞争对手

3.3实验结果与分析

3.3.1总体性能比较

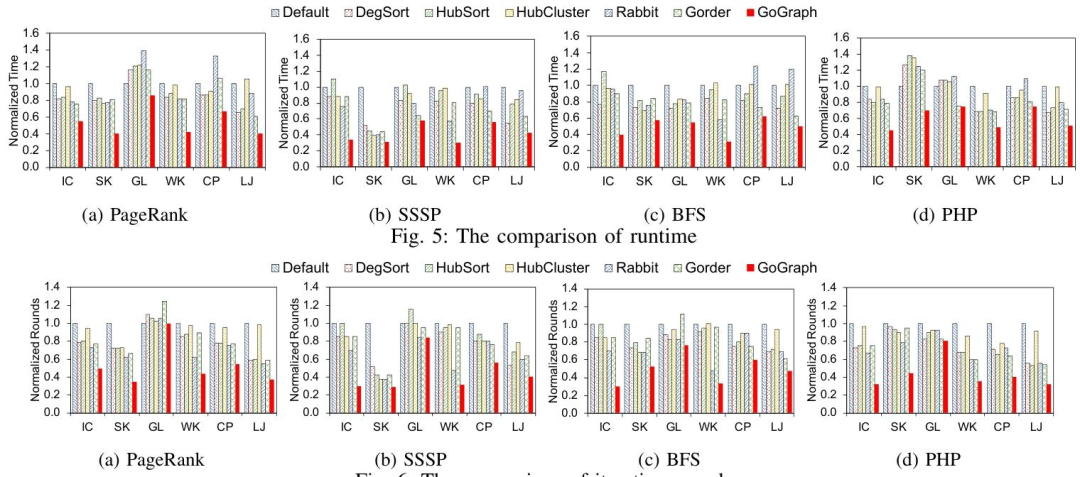
3.3.1.1运行时间比较

总体性能比较

实验结果表明，GoGraph在运行时间方面显著优于其他方法。具体来说：

• GoGraph平均运行时间比Default快2.10倍，最高可达3.33倍。

• GoGraph平均运行时间比Degree Sorting快1.66倍，最高可达2.75倍。

• GoGraph平均运行时间比Hub Sorting快1.85倍，最高可达3.24倍。

• GoGraph平均运行时间比Hub Clustering快1.93倍，最高可达3.34倍。

• GoGraph平均运行时间比Rabbit快1.80倍，最高可达2.42倍。

• GoGraph平均运行时间比Gorder快1.62倍，最高可达2.68倍。

3.3.1.2迭代轮数比较

在迭代轮数方面，GoGraph同样表现出色。具体来说：

• GoGraph平均减少的迭代轮数比Default多52%，最高可达71%。

• GoGraph平均减少的迭代轮数比Degree Sorting多39%，最高可达65%。

• GoGraph平均减少的迭代轮数比Hub Sorting多40%，最高可达70%。

• GoGraph平均减少的迭代轮数比Hub Clustering多45%，最高可达68%。

• GoGraph平均减少的迭代轮数比Rabbit多32%，最高可达57%。

• GoGraph平均减少的迭代轮数比Gorder多39%，最高可达67%。

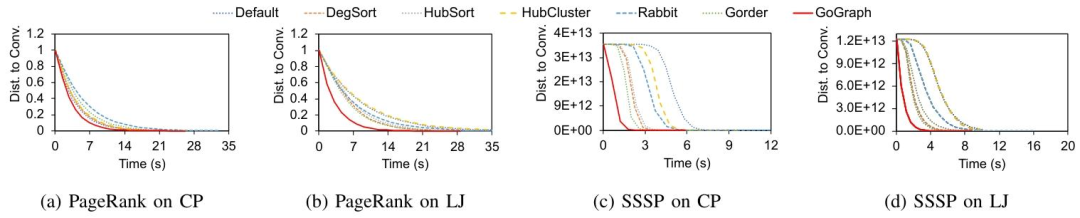
3.3.2收敛速度比较

为了评估GoGraph的收敛速度，实验在CP和LJ图上运行了PageRank和SSSP算法。结果表明，GoGraph在所有情况下都能更快地收敛。具体来说：

• GoGraph达到相同收敛状态所需的时间仅为其他算法平均时间的59%，最低可达37%。

• 在CP图上运行PageRank时，GoGraph的收敛速度明显快于其他方法。

• 在LJ图上运行PageRank时，GoGraph同样表现出更快的收敛速度。

• 在CP和LJ图上运行SSSP时，GoGraph的收敛速度也显著优于其他方法。

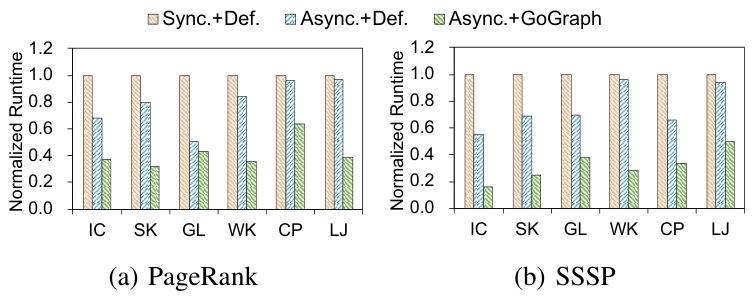
3.3.3异步更新模式的影响

实验还评估了异步更新模式和顶点处理顺序对迭代计算加速的影响。结果表明：

• 异步更新模式相比同步更新模式能够加速迭代计算。

• GoGraph在异步更新模式下表现出显著的性能提升，平均速度提升1.56倍至6.30倍。

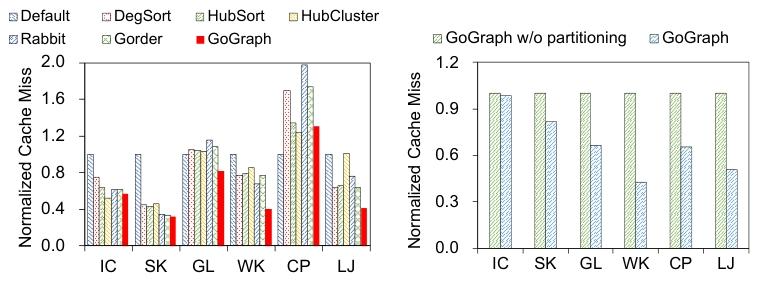
3.3.4CPU缓存缺失影响

缓存未命中的影响

GoGraph通过优化顶点处理顺序，减少了缓存缺失，提高了计算效率。具体来说：

• GoGraph平均可减少30%的缓存缺失，这意味着在从内存中读取图数据时，I/O开销显著降低。

• 通过图划分进一步减少了33%的缓存缺失，最高可达58%。

3.3.5度量函数的有效性

实验验证了度量函数M(·)的有效性。具体来说：

• 处理顺序的M(·)值越大，算法所需的迭代轮数越少。

• GoGraph产生的处理顺序的M(·)值最大，且所需的迭代轮数最少。

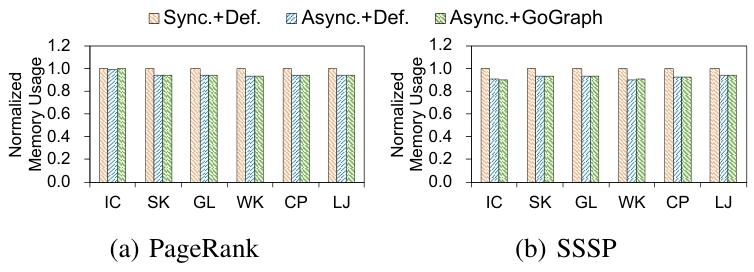
3.3.6内存使用情况

实验评估了不同迭代计算方法的内存使用情况。结果表明：

• GoGraph在内存使用方面与同步更新模式相当，不会显著增加内存开销。

• GoGraph通过重排序处理顺序，在不增加额外数据结构的情况下，提高了迭代计算的效率。

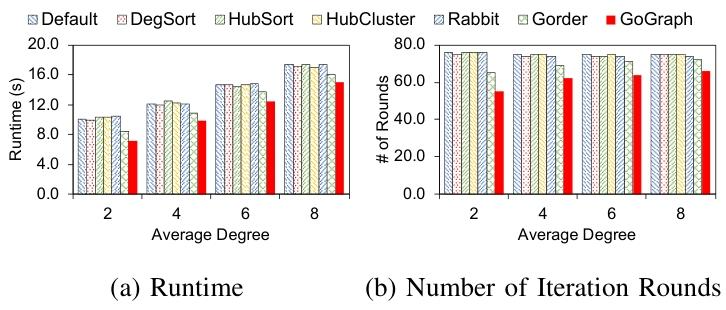
3.3.7平均度数的影响

实验还评估了平均图度数对GoGraph性能的影响。结果表明：

• GoGraph在不同平均度数的图上均表现出色，无论是运行时间还是迭代轮数。

• 随着平均度数的增加，PageRank的运行时间有所增加，但迭代轮数保持相似。

3.3.8不同划分方法的影响

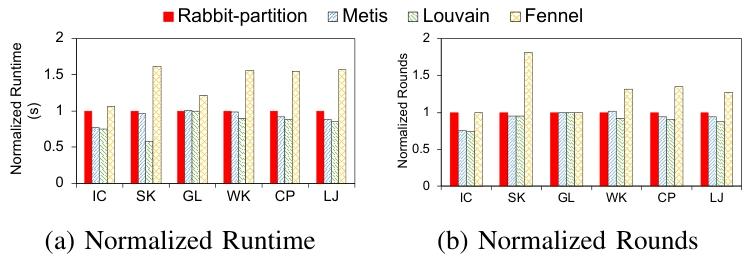
实验评估了不同图划分方法对GoGraph性能的影响。结果表明：

• 不同的划分方法对运行时间和迭代轮数有影响。

• Rabbit-Partition、Metis和Louvain表现出相似的性能，而Fennel由于其基于流的特性，性能较差。

  
  

3.4实验结论

3.4.1GoGraph的优势

GoGraph通过优化顶点处理顺序，显著减少了迭代轮数，提高了计算效率。实验结果表明，GoGraph在运行时间和迭代轮数方面均优于其他方法，特别是在大规模图数据上表现更为突出。

3.4.2实际应用价值

GoGraph的优化策略不仅适用于图计算，还可以扩展到其他类型的图算法和应用场景，为分布式计算和大数据分析提供更强大的支持。通过减少迭代轮数和优化内存访问模式，GoGraph在实际应用中能够显著提高计算效率，降低资源消耗。

4.1同步迭代优化

4.1.1传统同步迭代方法

传统的同步迭代方法在每一轮迭代中，所有顶点基于前一轮的状态进行更新。这种方法虽然在理论上具有简单性和一致性，但在实际应用中存在明显的效率问题。具体来说，同步迭代方法需要在每一轮迭代中进行全局的同步操作，这导致了较高的通信开销和时间延迟。特别是在大规模图数据上，这种同步操作的开销变得更加显著，限制了系统的扩展性和性能。

4.2.2异步计算模式的探索

为了解决同步迭代方法的不足，一些研究工作开始探索异步计算模式。例如，Priter和Maiter等方法通过优先选择特定的顶点进行迭代计算，避免了对所有顶点的无效计算。这些方法在一定程度上提高了计算效率，但通常需要用户定义的顶点选择策略，增加了使用难度。此外，异步计算模式可能引入不稳定性，特别是在处理大规模图数据时，可能导致收敛速度变慢或结果不准确。

4.2图重排序

4.2.1顶点重排序的重要性

顶点重排序是图数据预处理的一个重要环节，旨在通过提高顶点的局部性来增强内存访问效率。Gorder、Rabbit、Hub Clustering和Hub Sorting等方法通过不同的方式对顶点进行重排序，以提高缓存命中率和加速迭代。这些方法在一定程度上改善了图计算的性能，但仍然存在改进的空间。

4.2.2现有重排序方法的不足

现有的图重排序方法虽然在提高内存访问效率方面取得了一定的成果，但在减少迭代轮数方面仍有不足。例如，Gorder方法通过滑动窗口计算有序顶点和无序顶点之间的分数，但这种方法在处理大规模图数据时可能面临计算复杂度高的问题。Rabbit方法通过将频繁访问的顶点映射到L1缓存附近，减少了缓存行交换的开销，但在处理高阶顶点和孤立顶点时可能不够高效。Hub Clustering和Hub Sorting方法通过将中心性较高的顶点聚类或排序，提高了图的局部性，但在全局优化方面可能不够全面。

4.3GoGraph算法的创新之处

4.3.1度量函数的设计

GoGraph算法引入了一个度量函数M(OV)，用于量化顶点处理顺序在加速迭代计算方面的效率。该函数通过计算源顶点在目的顶点之前的边数来反映处理顺序的质量。通过最大化M(OV)，GoGraph确保更多顶点能在迭代中利用邻居的最新状态，从而加快收敛速度。

4.3.2分治策略的应用

GoGraph采用分治策略进行顶点重排序，具体步骤包括提取高阶顶点和孤立顶点、划分剩余顶点、在子图内重排序顶点、重排序子图以及插入高阶和孤立顶点。这种方法不仅降低了重排序的复杂度，还能够有效地优化全局处理顺序，提高计算效率。

4.3.3实验验证与性能提升

GoGraph算法在多个真实世界的数据集上进行了实验验证，结果表明其在运行时间和迭代轮数方面均优于其他方法。GoGraph通过减少迭代轮数和优化内存访问模式，显著提高了计算效率，降低了系统的资源消耗。

5.1未来展望

5.1.1更高效的图划分方法

未来的研究可以进一步探索更高效的图划分方法，以更好地保持顶点的局部性和减少全局重排序的复杂性。例如，可以结合机器学习技术，自动学习图的结构特性，从而实现更智能的图划分。

5.1.2结合硬件特性优化

GoGraph可以进一步结合硬件特性进行优化，如利用多核处理器的并行计算能力、优化内存访问模式等，以进一步提高计算效率。特别是在分布式计算环境中，如何充分利用硬件资源，减少节点之间的通信开销，是一个重要的研究方向。

5.1.3扩展到其他图算法

GoGraph的优化策略可以扩展到其他类型的图算法，如图神经网络、社区检测等。在这些领域，通过优化顶点处理顺序，可以提高算法的收敛速度和计算效率，为复杂图数据分析提供更有效的解决方案。

5.1.4实时图分析的应用

对于需要实时响应的图分析任务，如欺诈检测、网络安全监控等，GoGraph能够通过减少迭代轮数，加快计算速度，满足实时性要求。未来可以进一步探索GoGraph在实时图分析中的应用，开发更高效的实时图计算框架。

5.1.5跨领域应用的探索

GoGraph的优化思想不仅限于图计算领域，还可以应用于其他需要迭代计算的场景，如机器学习、数据挖掘等。通过优化数据处理顺序，提高迭代计算的效率，可以为这些领域的发展提供新的思路和方法。

5.2总结

GoGraph算法通过优化顶点处理顺序，显著提高了迭代计算的效率。其创新的度量函数和分治策略为图重排序提供了新的解决方案。通过实验验证，GoGraph在多个方面表现出色，具有重要的实际应用价值。未来的研究可以进一步优化图划分方法，结合硬件特性，扩展到其他图算法和应用场景，为大数据分析和分布式计算提供更强大的支持。

论文解读联系人：

刘思源

13691032906（微信同号）

liusiyuan@caict.ac.cn