首先为大家推荐这个 OceanBase 开源负责人老纪的公众号,后续会持续更新和 AI 相关的各种技术内容。欢迎感兴趣的朋友们关注!默而识之,学而不厌,诲人不倦,何有于我哉?
——《论语 · 述而》
AI 时代离不开向量数据库,身边也有不少人都开始分享相关的知识。
前两天读了洪波老师在老纪这个公众号里发表的一篇文章《OceanBase 支撑 AI 规模化落地的关键路径及应用案例》,又学到不少新东西。但其中提到了很多专业词汇,需要 AI 数据库爱好者在了解向量数据库之前,已经有过一些相关的知识储备才能看懂。
今天就集中学习了上面这篇文章中出现的各种生词,速记如下,于此和大家进行分享。本文没有阅读门槛,浅显易懂,适合大家对向量数据库进行“浅入了解”。如果有朋友希望能够继续深入学习,这篇文章也可以作为一个很好的引子。
即将为大家解释的和向量数据库相关的基础概念如下:
1. Embedding 2. 距离 相似性度量 Cosine_distance Inner_product L1_distance L2_distance Jaccard Distance Hamming distance 3. 相似性搜索算法 典型算法 倒排 + 数据压缩 导航图索引 + 分布式 HNSW IVF DiskANN 4. 索引压缩算法 SQ(Scalar Quantization) PQ(Product Quantization)
5. 召回率
正文开始:
向量数据库这个概念有点儿老生常谈了。简单说就是:在数据库中用多维向量存储某类事物的特征,通过公式计算各个向量在空间中的位置关系,判断事物之间的相似性。
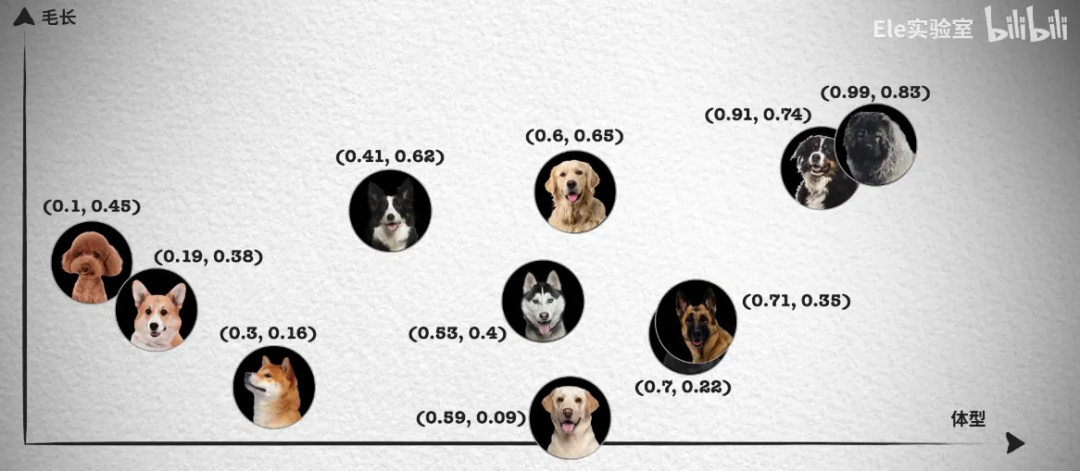
一个对象可以抽取多种正交的特征,比如(体型、毛长等),每个特征代表向量的一个维度。 每个维度的精度越细,区分度越高。 维度数越多,区分度越高,相似性查询也越精确。同时,计算量和查询空间也会更大。
1. Embedding
通过深度学习神经网络提取非结构化数据里的内容和语义,把图片、视频等变成特征向量,这个过程叫 Embedding。
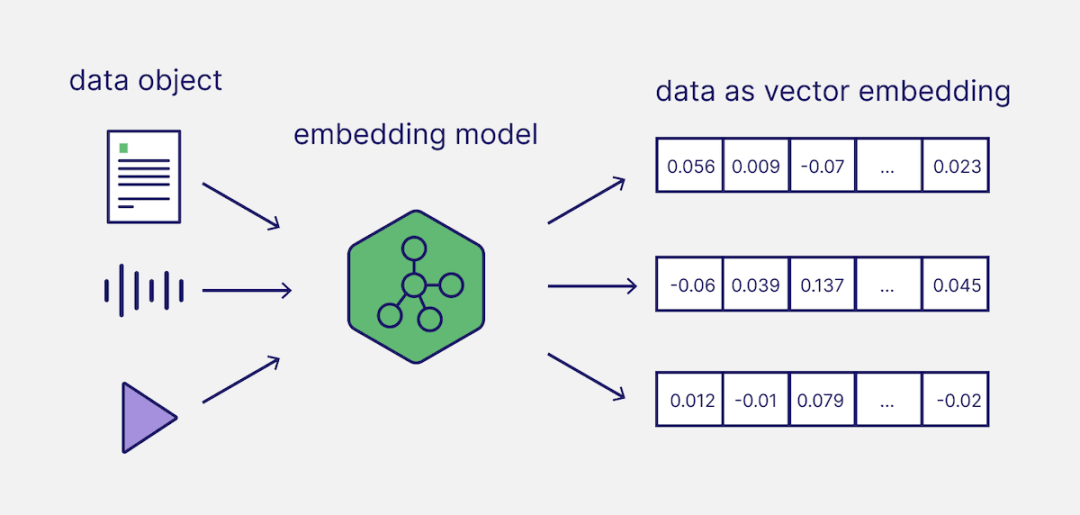
Embedding 技术将具有丰富特征的多模态数据(文字、图片、音频、视频),转换为多维数组(向量)。然后 AI 应用就可以通过向量距离来做计算,进而判断原始多模态数据的相似性。
2. 距离 相似性度量
常见的相似度测量方式会涉及到一些中学数学的基础知识,例如:余弦相似度、内积(点积)、欧几里得距离(欧式距离)、曼哈顿距离。让我们一起来复习下,追忆一下逝去的青春。以下这部分内容参考自 OceanBase 官网文档《向量函数》[1]。
2.1 Cosine_distance
余弦相似度(cosine similarity):计算两个向量间夹角的余弦值。当两个向量方向相同时余弦相似度的值为 1;当两个向量夹角为 90 度时余弦相似度的值为 0,当两个向量方向完全相反时余弦相似度的值为 -1。
余弦相似度的计算公式为:
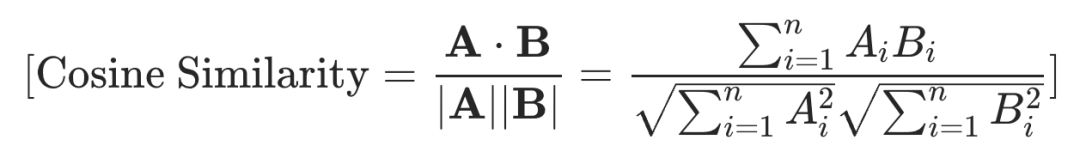
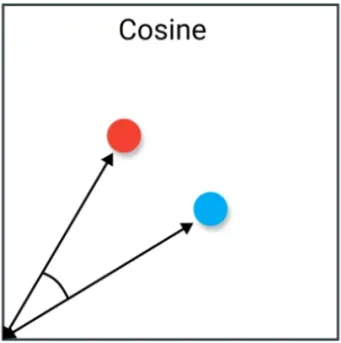
由于余弦相似度度量越接近于 1 表示越相似,因此有时也使用余弦距离(或余弦不相似度)作为向量间距离的一种衡量方式,余弦距离可以通过 1 减去余弦相似度来计算:
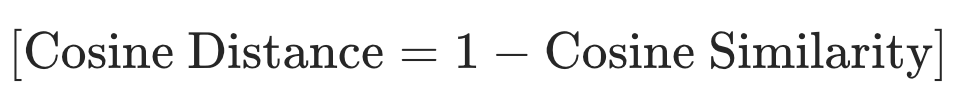
余弦距离的取值范围是 [0, 2],其中 0 表示完全相同的方向(无距离),而 2 表示完全相反的方向。
2.2 Inner_product(IP 内积)
内积又称为点积或数量积,是线性代数中的一种重要运算,它定义了两个向量之间的一种乘积。在几何意义上,内积表征了两个向量的方向关系和大小关系。
计算公式为:
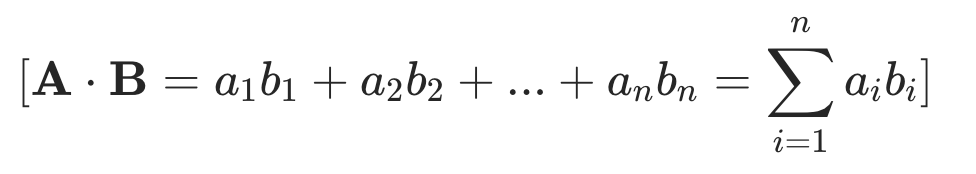
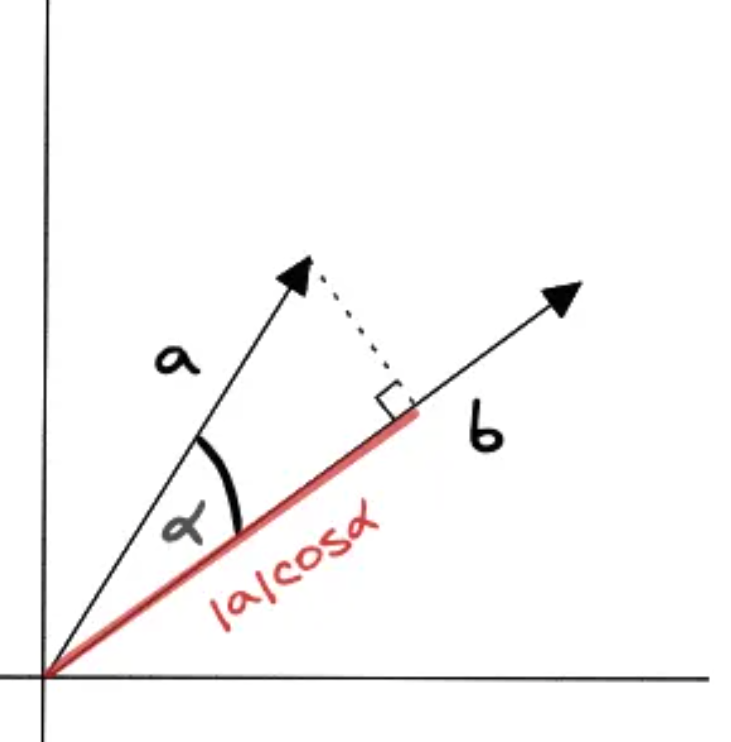
2.3 L1_distance
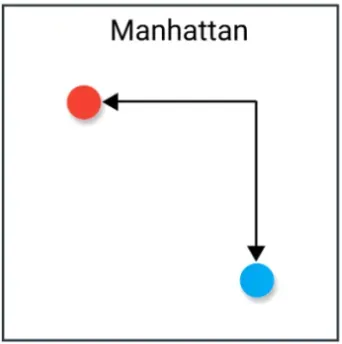
曼哈顿距离(Manhattan Distance)用于计算两个点在标准的坐标系中的绝对轴距总和。
计算公式为:
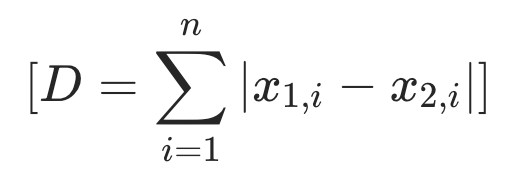
2.4 L2_distance
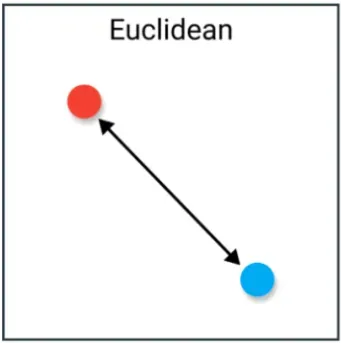
欧几里得距离(Euclidean Distance)反映的就是两个向量之间的直线距离,计算向量在各个维度差值的平方和的平方根即可。
计算公式为:
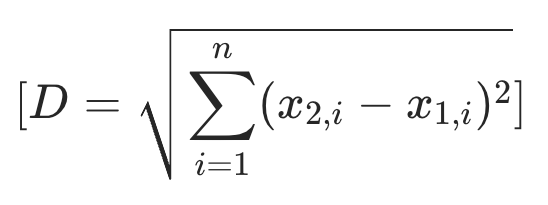
2.5 总结
Cosine(余弦距离):通过计算两个向量之间的夹角余弦值来衡量它们的相似程度,取值范围为 [-1, 1],值越接近 1 表示越相似。 IP (Inner Product,内积):两个元素的对应元素相乘并求和的结果计算相似度,内积值越大相似度越高. 通常在自然语言处理(NLP)领域中使用。 L1(曼哈顿距离):曼哈顿距离是两个向量各个维度差值的绝对值之和。与欧氏距离不同,曼哈顿距离更关注各个维度的差异,而不是方向。 L2(欧式距离):欧氏距离是两个向量之间的直线距离,可以表示为它们各个维度差值的平方和的平方根。欧氏距离越小,表示两个向量越相似。通常在自然语言处理(NLP)领域中使用。
2.6 What's more?
接下来为大家介绍两个针对二值向量的常用相似性度量方法。
二值向量即向量中的每个元素要么是 0,要么是 1。二值向量的实现方式相比浮点向量也会有所不同,为了节省空间,数据库内部往往会用 byte 而非 float 来实现二值向量。
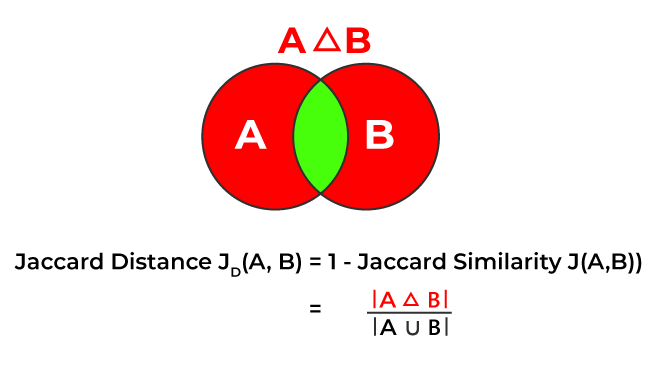
2.6.1 Jaccard Distance
杰卡德距离,计算的是两个集合并集中,不属于交集的元素的比例,用于反映差异度。
公式如下:
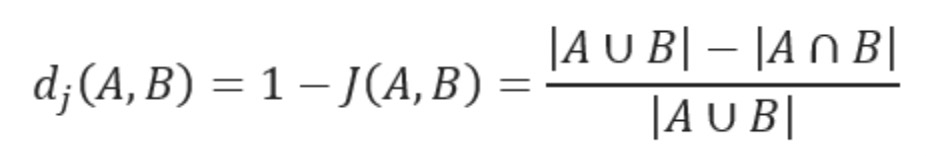

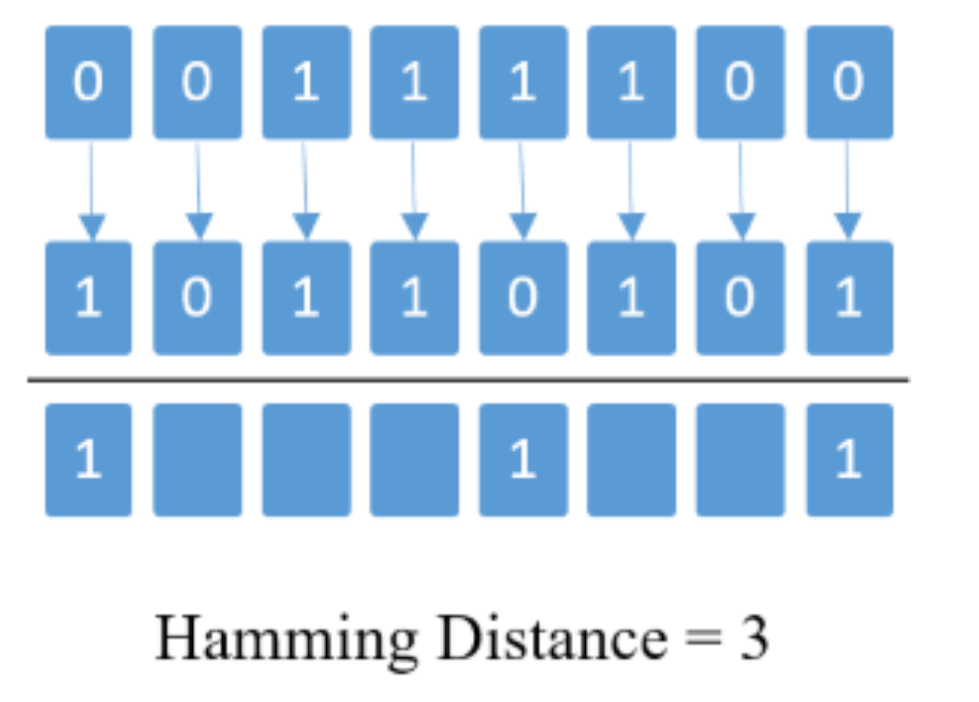
2.6.2 Hamming distance
汉明距离(Hamming distance)是数据传输差错控制编码中的概念,表示了两个字对应位不同的数量,定义为将两个字进行异或运算后 1 的位数。
3. 相似性搜索算法
向量数据库相似性搜索,是通过计算输入向量与目标向量的相似度,快速找出与输入向量最相似数据的搜索技术。这其中以 Approximate Nearest Neighbor(近似最近邻,ANN)搜索和以 K-Means 为代表的聚类搜索最具代表性。
3.1 典型算法
3.1.1 倒排 + 数据压缩
通过聚类算法(常用 K-Means 算法)将数据分为若干聚簇,按照聚簇中心建立倒排索引。每次搜索时,先计算与聚簇中心的相似度,选择相似性最高聚簇进一步搜索。
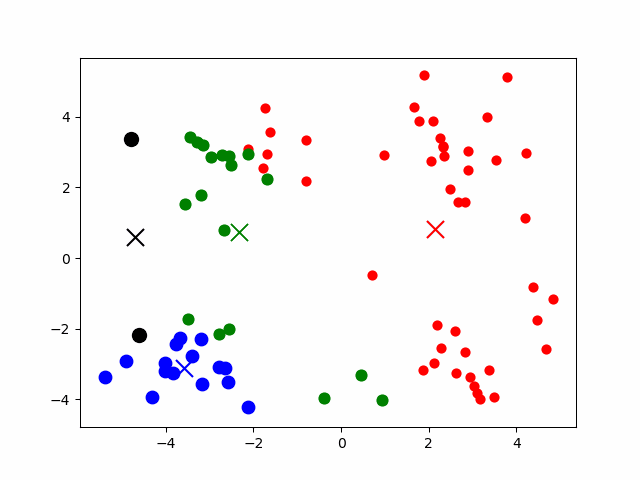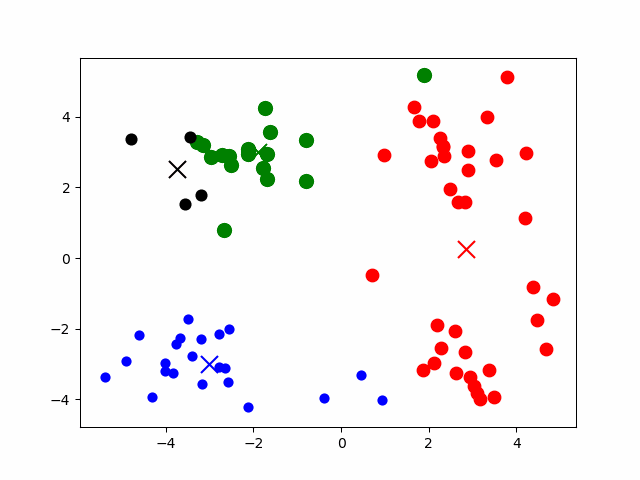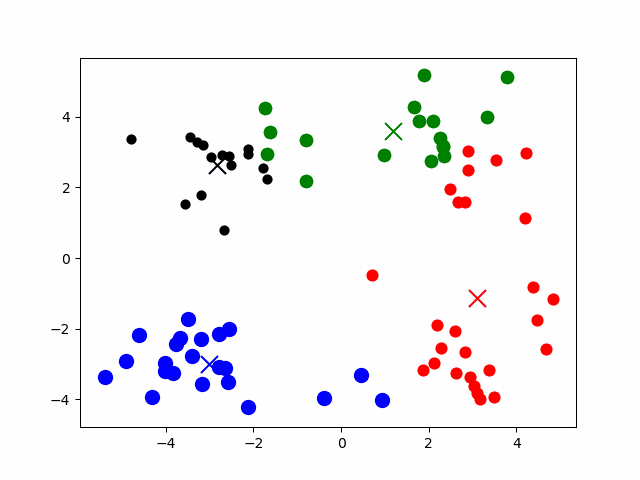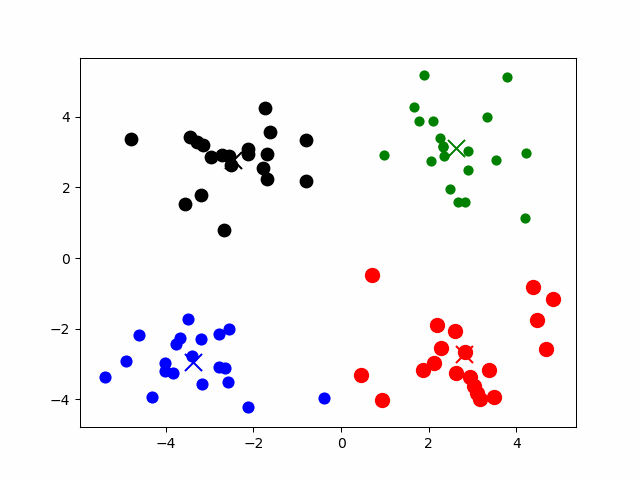
3.1.2 导航图索引 + 分布式
将向量作为点,向量相似度作为边,建立近似近邻图,在图上进行贪心搜索逼近近邻区域。
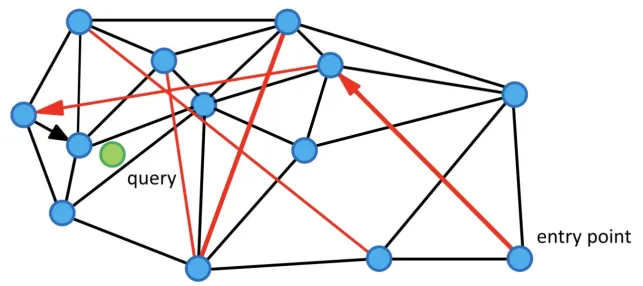
图索引在内存中最高效,但对内存占用较大,所以经常会基于分区以及分布式的方式,来解决大数据量的问题。
优点是能够实现高召回率以及低延迟(思路类似六度分隔理论 —— 最多通过六个人,你就能够认识任何一个陌生人)。缺点也很明显,就是成本高。
3.2 HNSW
Hierarchical Navigable Small World(分层导航小世界)是介于规则图和随机图之间的一种图结构,其特点是每个节点仅与很小有限的节点有联系,并且这些节点有一定的集中性。小世界图中大部分节点彼此并不联系,但大部分节点经过几步即可到达。HNSW 是基于 “邻居的邻居可能是邻居” 的核心思想, 社交网络便是典型的小世界图结构。咱们先看一个大家都更熟悉的数据结构 —— 跳表 SkipList。
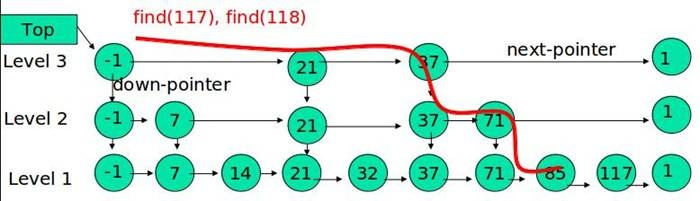
跳表是典型的用空间换取时间,索引分了好几层,最底层(图中 Level1)存储了所有的数据,而上面几层,则存储了指向某几个数据的索引,且越往上索引数量越少。跳表的作用就是:先快速的接近要查找的点的附近,然后再精确的搜索,这样就避免了路上做很多无用功耽误时间。个人理解,HNSW 就是将跳表运用在了图结构中。
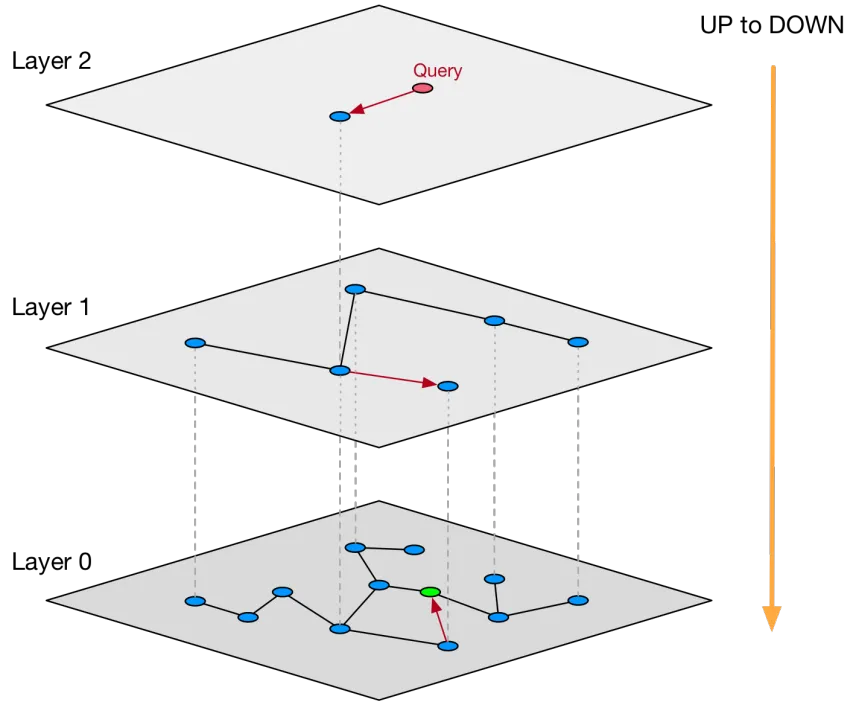
跳表的每一层,都是一个小世界网络。其中最底层(Layer = 0)是一个完整的 NSW(导航小世界网络),其它层存储的则是指向图节点的指针索引。使用类似于跳表的原因也很简单,为了少做无用功耽误时间。
上层小世界图可以看成是下层的缩放,多层图的方式目的是为了减少搜索时距离计算和比较的次数。检索时,从最高一层(即最稀疏的一层)开始,每一层得到的检索结果再作为下一层的输入,如此,不断迭代到最后一层。最后得到查询点的 K 个近邻。
HNSW 是目前最流行的向量检索算法,性能和召回率都比较不错,但是对内存有强依赖。
3.3 IVF
IVF(Inverted File Index)索引通过聚类算法将向量空间划分为多个子空间,并为每个子空间建立索引。在搜索过程中,IVF 索引首先根据查询向量找到其所属的子空间(下图中红框表示子空间),然后在对应子空间中进行精确搜索。
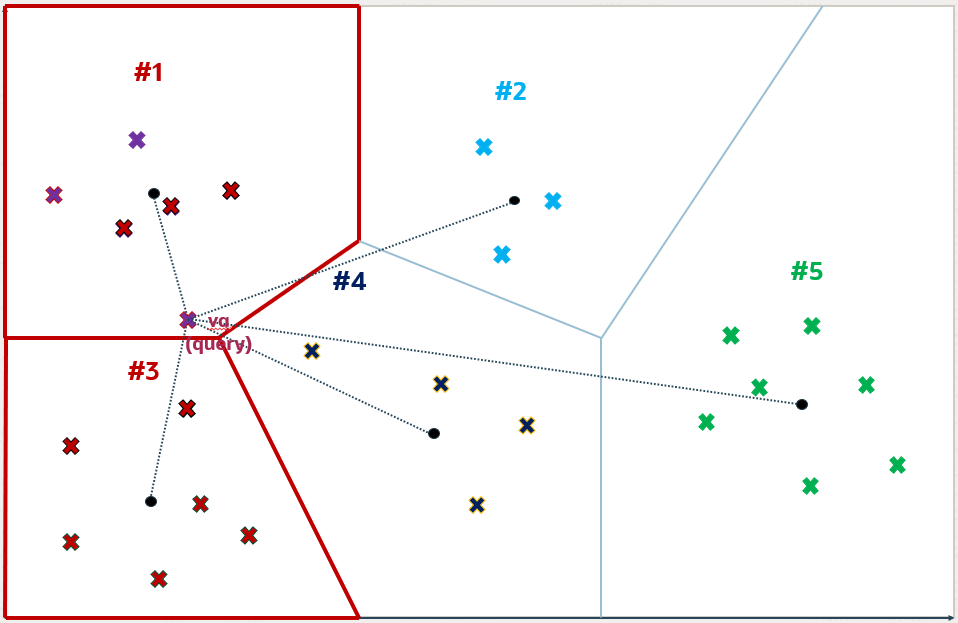
优点是搜索速度快。缺点是召回率不优,因为聚类中心是预建的,增量数据的导入不会影响聚类中心的分布,数据更新后,需要依赖聚类的重建。
3.4 DiskANN
期望解决的问题:
如何能够减少访问磁盘的频率?先访问内存,只有真正需要原始向量时再去访问磁盘。 如何组织数据结构?保证一次读盘操作便可以取出相关的节点边图信息。
DiskAnn 的思路:
DiskANN 算法结合了两类算法 —— 聚类压缩算法和图结构算法。 算法如下: 通过压缩原始数据,仅将压缩后的码表信息和中心点映射信息放到内存中。而原始数据和构建好的图结构数据存放到磁盘中,只需在查询匹配到特定节点时到磁盘中读取。 修改向量数据和图结构的排列方式,将数据点与其邻居节点并排存放,这种方式使得一次磁盘操作即可完成节点的向量数据、邻接节点等信息的读取。
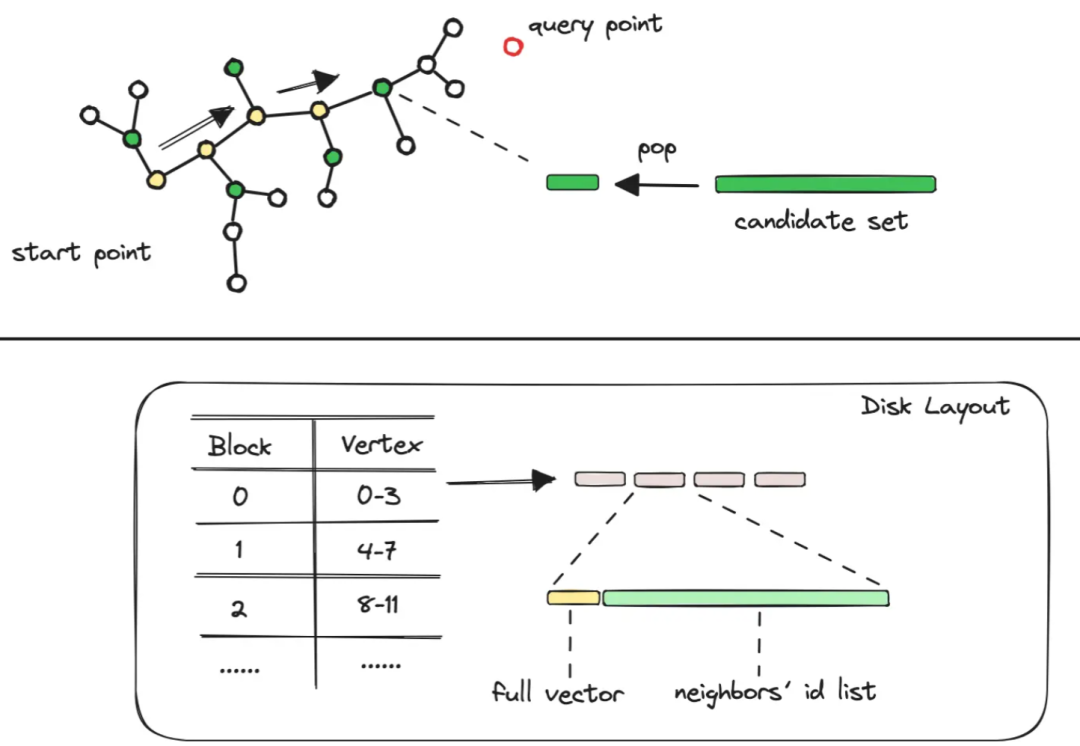
DiskANN 算法的优点和缺点多很明显:
优点:大幅提升向量召回的读取效率,降低图算法的内存,提升召回率。 缺点:索引的构建开销较大,更适合静态数据集(或者不经常变的数据集合)。
4. 索引压缩算法
Quantized 是将现有的索引(如IVF、HNSW)与量化等压缩方法结合起来,以减少内存占用并加快搜索速度。
向量的压缩, 一般是基于降低向量维度,降低向量元素的精度的思路,分为两类:标量量化(Scalar Quantization,SQ)和乘积量化(Product Quantization,PQ)。例如 IVF-PQ、HNSW-PQ。
4.1 SQ(Scalar Quantization)
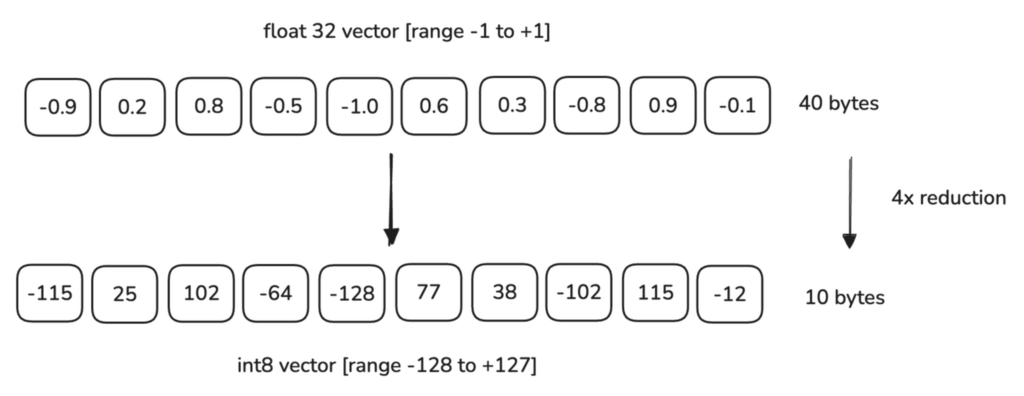
思想是:把一个高精度的浮点向量,主动丢失部分精度,变为一个低精度向量,减少计算和存储开销。例如把向量中的元素 0.1192 和 0.1365 统一用 0.1 来替换。
大致原理(可选择性阅读):
分割范围:首先确定向量中数值的大致范围,然后将这个范围分成若干个等间隔的小段或桶(这称为量化级别或量化步长)。 映射值:将原始向量中的每个元素映射到最近的一个桶中。具体来说,就是将每个浮点数值舍入到其最近的量化级别的中心值,这个过程通常称为量化。 编码:被映射到各个桶中的值可以用更紧凑的形式表示,例如,用桶的索引(一个整数)来代替原始的浮点数,从而实现压缩。
4.2 PQ(Product Quantization)
思想是:把高维向量空间降维。因为低维向量的存储和计算开销都远远低于高维。
大致原理(可选择性阅读):
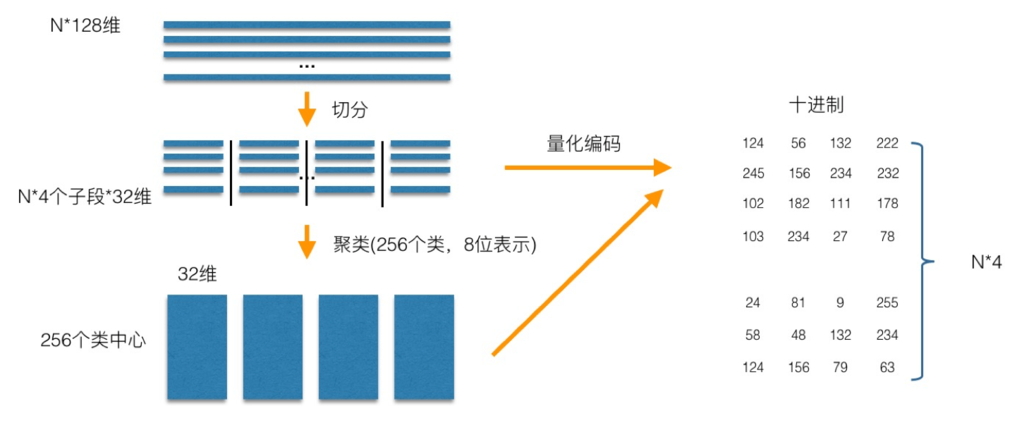
分组(Dimension Splitting):首先,将原始的高维向量空间分成多个子空间,通常是将 d 维向量分为 m 个大小相等的子集,每个子集包含 d / m 维。这样做的目的是将一个复杂的高维问题分解为多个较低维度的问题,便于处理。 量化编码(Codebook Generation):对于每个子空间,构建一个码本(codebook)。码本是一个由 k 个向量组成的集合,这些向量是该子空间内所有训练向量的聚类中心。这一步通常通过聚类算法完成,每个子空间的向量被分配到离它最近的聚类中心。 编码(Encoding):对于每一个高维向量,将其在每个子空间上的投影与相应的码本进行比较,找出距离最近的码本向量,并记录下这个向量在码本中的索引。这样,原始的高维向量就被转换为了一个长度为 m 且每个元素范围在 0 到 k - 1 之间的整数序列,即可得到一个紧凑的量化表示。
4. 索引压缩算法
Quantized 是将现有的索引(如IVF、HNSW)与量化等压缩方法结合起来,以减少内存占用并加快搜索速度。
向量的压缩, 一般是基于降低向量维度,降低向量元素的精度的思路,分为两类:标量量化(Scalar Quantization,SQ)和乘积量化(Product Quantization,PQ)。例如 IVF-PQ、HNSW-PQ。
4.1 SQ(Scalar Quantization)
思想是:把一个高精度的浮点向量,主动丢失部分精度,变为一个低精度向量,减少计算和存储开销。例如把向量中的元素 0.1192 和 0.1365 统一用 0.1 来替换。
大致原理(可选择性阅读):
分割范围:首先确定向量中数值的大致范围,然后将这个范围分成若干个等间隔的小段或桶(这称为量化级别或量化步长)。 映射值:将原始向量中的每个元素映射到最近的一个桶中。具体来说,就是将每个浮点数值舍入到其最近的量化级别的中心值,这个过程通常称为量化。 编码:被映射到各个桶中的值可以用更紧凑的形式表示,例如,用桶的索引(一个整数)来代替原始的浮点数,从而实现压缩。

4.2 PQ(Product Quantization)
思想是:把高维向量空间降维。因为低维向量的存储和计算开销都远远低于高维。
大致原理(可选择性阅读):
分组(Dimension Splitting):首先,将原始的高维向量空间分成多个子空间,通常是将 d 维向量分为 m 个大小相等的子集,每个子集包含 d / m 维。这样做的目的是将一个复杂的高维问题分解为多个较低维度的问题,便于处理。 量化编码(Codebook Generation):对于每个子空间,构建一个码本(codebook)。码本是一个由 k 个向量组成的集合,这些向量是该子空间内所有训练向量的聚类中心。这一步通常通过聚类算法完成,每个子空间的向量被分配到离它最近的聚类中心。 编码(Encoding):对于每一个高维向量,将其在每个子空间上的投影与相应的码本进行比较,找出距离最近的码本向量,并记录下这个向量在码本中的索引。这样,原始的高维向量就被转换为了一个长度为 m 且每个元素范围在 0 到 k - 1 之间的整数序列,即可得到一个紧凑的量化表示。

5. 召回率
最后再来一个大家都可以轻松理解的概念 —— 召回率。
召回率是说:检索出来的结果集中, 接近目标向量的结果比例。召回率 = 真正例 / (真正例 + 假反例)。
暴力搜索的召回率可以100%,但是基本不可接受。基于向量索引搜索的召回率一般低于 100%,是一个非精确的搜索。召回率和向量索引的组织算法,压缩(压缩的本质是通过降低精度,减少计算开销)算法等相关。
这篇文章到此为止。作者能力有限,欢迎大家批评指正!
和向量数据库相关的内容,以后有缘再更。
OceanBase 官网文档《向量函数》: https://www.oceanbase.com/docs/common-oceanbase-database-cn-1000000002012938






