前言
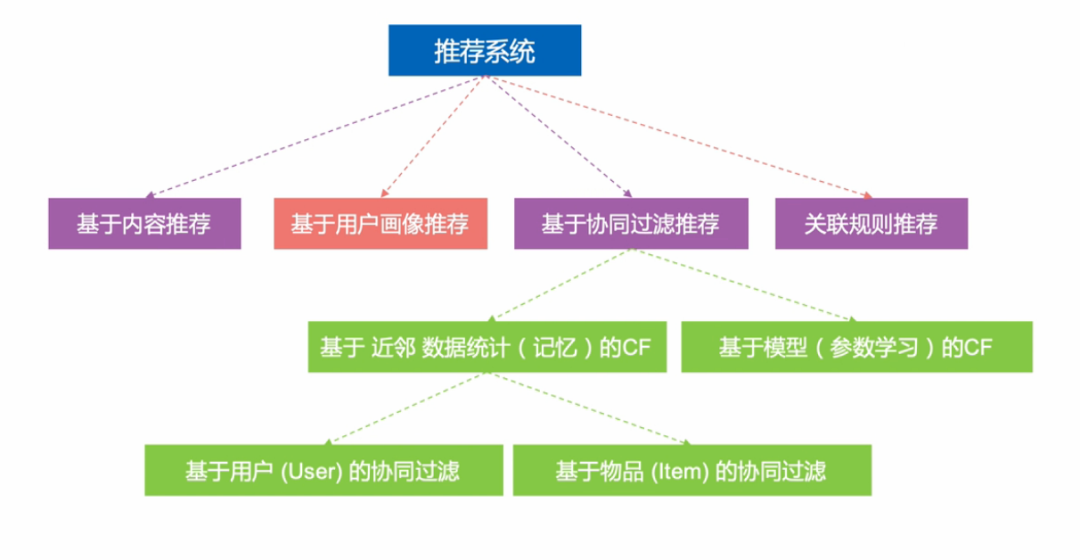
基于模型协同过滤的核心思想
基于模型的协同过滤推荐就是基于样本的用户喜好信息,训练一个推荐模型,然后根据实时的用户喜好的信息进行预测计算推荐。
基于模型的推荐算法,是与基于记忆的推荐算法相对的基于记忆的推荐算法,主要是将所有的用户数据读入内存,进行运算;当数据量特别大时,显然这种方法是不靠谱的,因此出现了基于模型的推荐算法,依托于一些机器学习的模型,通过离线进行训练,在线进行推荐。
■ 基于模型推荐系统的优势:
(1)节省空间: 一般情况下,学习得到的模型大小远小于原始的评分矩阵,所以空间需求通常较低。
(2)训练和预测速度快:基于近邻的方法的一个问题在于预处理环节需要用户数或物品数的平方级别时间,而基于模型的系统在建立训练模型的预处理环节需要的时间往往要少得多。在大多数情况下,压缩和总结模型可以被用来加快预测。
矩阵分解详解
* 算法分类
基于模型的协同过滤作为目前最主流的协同过滤类型,当只有部分用户和部分物品之间是有评分数据的,其它部分评分是空白,此时我们要用已有的部分稀疏数据来预测那些空白的用户和物品之间的评分关系,找到最高评分的物品推荐给用户。
基于模型协同过滤的方法的包括:
用关联算法
聚类算法
分类算法
回归算法
神经网络图模型以及隐语义模型来解决
基于模型协同近滤——矩阵分解模型
■ 基本思想
矩阵分解,直观上来说就是把原来的大矩阵,近似分解成两个小矩阵的乘积,在实际推荐计算时不再使用大矩阵,而是使用分解得到的两个小矩阵。按照矩阵分解的原理,我们会发现原来mxn的大矩阵会分解成mxk和kxn的两个小矩阵,这里多出来一个k维向量,就是隐因子向量(Latent Factor Vector),类似的表达还有隐因子、隐向量、隐含特征、隐语义、隐变量等。
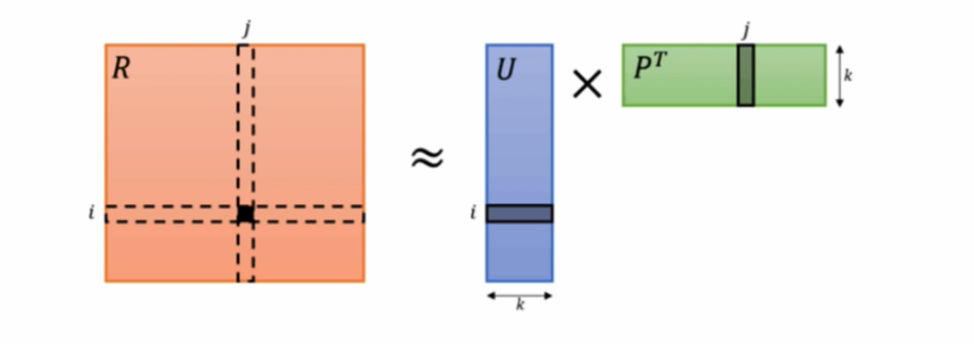
■ 基本思想
基于矩阵分解的推荐算法的核心假设是用隐语义(隐变量)来表达用户和物品,他们的乘积关系就成为了原始的元素。这种假设之所以成立,是因为我们认为实际的交互数据是由一系列的隐变量的影响下产生的,这些隐变量代表了用户和物品一部分共有的特征,在物品身上表现为属性特征,在用户身上表现为偏好特征,只不过这些因子并不具有实际意义,也不一定具有非常好的可解释性,每一个维度也没有确定的标签名字,所以才会叫做“隐变量"。而矩阵分解后得到的两个包含隐变量的小矩阵,一个代表用户的隐含特征,一个代表物品的隐含特征,矩阵的元素值代表着相应用户或物品对各项隐因子的符合程度,有正面的也有负面的。
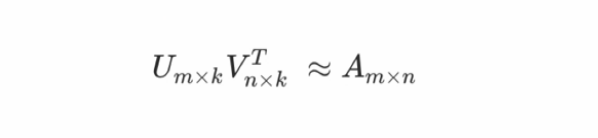
■ 矩阵分解过程——举例
根据如下的计算公式,我们来举例:

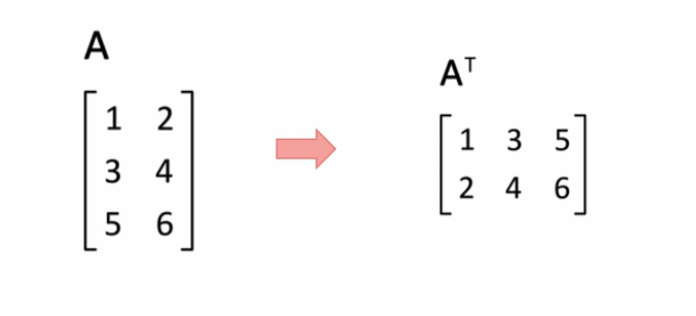
■ 矩阵分解过程——举例 矩阵的转置( transpose )
矩阵的转置(transpose) 是最简单的一种矩阵变换。简单来说,若m*n的矩阵M的转置记为M^T;则M^T是一个n*m的矩阵,并且M i,j = M^T j,i。因此,矩阵的转置相当于将矩阵按照主对角线翻转;同时,我们不难得出M= (M^T)^T。
■ 矩阵分解过程——举例
使用之前的用户-电影评分表,5个用户(U表示), 6个电影(M表示)。现在假设电影的风格有以下几类:喜剧,动作,恐怖。分别用K1、K2、K3 来表示。那么我们希望得到用户对于风格偏好的矩阵U,以及每个风格在电影中所占比重的矩阵M。
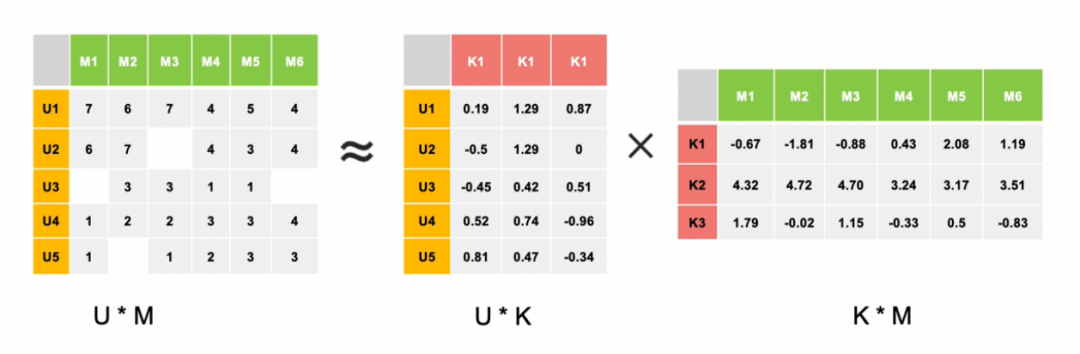
通常情况下,隐因子数量k的选取要远远低于用户和电影的数量,大矩阵分解成两个小矩阵实际上是用户和电影在k维隐因子空间上的映射,这个方法其实是也是一种“降维”(Dimension Reduction)过程。
■ 矩阵分解的目标
我们再从机器学习的角度来了解矩阵分解,我们已经知道电影评分预测实际上是一个矩阵补全的过程,在矩阵分解的时候原来的大矩阵必然是稀疏的,即有一部分有评分,有一部分是没有评过分的,不然也就没必要预测和推荐了。
所以整个预测模型的最终目的是得到两个小矩阵,通过这两个小矩阵的乘积来补全大矩阵中没有评分的位置。所以对于机器学习模型来说,问题转化成了如何获得两个最优的小矩阵。因为大矩阵有一部分是有评分的,那么只要保证大矩阵有评分的位置(实际值)与两个小矩阵相乘得到的相应位置的评分(预测值)之间的误差最小即可,其实就是一个均方误差损失,这便是模型的目标函数。
■ 矩阵分解的优势
比较容易编程实现,随机梯度下降方法依次迭代即可训练出模型。比较低的时间和空间复杂度,高维矩阵映射为两个低维矩阵节省了存储空间,训练过程比较费时,但是可以离线完成;评分预测一般在线计算,直接使用离线训练得到的参数,可以实时推荐。
预测的精度比较高,预测准确率要高于基于领域的协同过滤以及内容过滤等方法。
■ 矩阵分解的缺点
模型训练比较费时。
推荐结果不具有很好的可解释性,分解出来的用户和物品矩阵的每个维度无法和现实生活中的概念来解释,无法用现实概念给每个维度命名,只能理解为潜在语义空间。
■ 矩阵分解的作用
矩阵填充 (通过矩阵分解来填充原有矩阵,例如协同过滤的ALS算法就是填充原有矩阵)
清理异常值与离群点
降维、压缩
个性化推荐
间接的特征组合(计算特征间相似度)

扫描二维码 关注我们
微信号 : BIGDT_IN







