背景
数据库系统以及搜索引擎里面在索引的构建里面会使用到set的概念,比如符合某种条件的document的ID的set。对于集合的操作除了增/删元素,也需要针对集合做集合的union和intersection操作。而实现一个integer set的一个典型的方案是使用bitmap(或者叫bitset,bit vector):使用一个n位的数字,每一位表示对应的数字的是否存在于这个集合中,这个n位的数字可以容纳[0-n]的数字范围,集合之间的union, intersection可以用位操作AND, OR, AND NOT来高效的实现,在合适的场景下使用bitmap的效率要比其它的解法效率高很多。
但是这种“naive”的方法在以下两种情况下不大适用:
过多的元素存在于整个取值空间。
有大量连续存在的数字: S = {1,2,3,4....99,100}: 这种通过RLE压缩效率会很高。
针对这种“naive”方式的改进是使用RLE进行压缩:
比如S = {1,2,3,4....99,100}:可以表示成{[1,99]}表示从1开始,后面还有连续的99个数字。
再比如S={1,2,3,4....99,100,200,201...210}表示成{[1,99],[200,10]}
这种方式占用的内存空间要比“naive”的方式要小很多。Oracle BBC(Word长度是8),EWAH,COMPAX,Concise(Word长度是32或者64)走的都是这路线。RLE压缩的bitmap的弊端在于效率不高:
要检查一个元素是否存在于bitmap里面,需要检查整个bitmap
要计算两个run个数分别为B1和B2的bitmap的intersection,复杂度是O(B1 + B2), 这个是比hashset的效率要差的。
如果是两个cardinality分别是S1和S2的两个hashset,计算intersection只要遍历较小的那个set看每个元素是否存在于大的set里面,因此复杂度是O(min(S1, S2))。
而Roaring Bitmap则是对这些前辈的改进,Roaring Bitmap底层综合了三种不同的存储形式:不压缩的bitmap,使用integer array“压缩”的bitmap,以及使用RLE(run-length encoding)压缩的bitmap。这种新的bitmap压缩格式比别的格式(WAH,Concise,EWAH)更快,可以从两倍到2个数量级,而压缩率又更高。
Roaring Bitmap的结构
首先它是一个两层结构,或者说Key-Value结构,Key是一个16位的数字,Value是这个16位数字对应的Chunk。在第一层里面会把整个取值空间切分成大小为2 ^ 16的一个个chunk。在每个chunk里面会根据当前chunk里面元素的稠密情况决定使用不同的容器类型以提高效率
如果元素比较多,比较稠密(元素的个数大于4096),那么使用传统的不压缩的bitmap结构,占用空间是 216 个bit,也就是8KB。这个216的空间被分成了1024个word,每个word是64位。这个Container同时还会保存一个计数器记录多少个位被设为了1。要去检查一个数字里面有多少位是1的话如果实现的挫的话可能性能会很差的,现代的处理器其实都有专门的bitCount指令来高效的做这种事情,比如X64里面的popcnt,ARM架构的cnt,对应到Java语言里面是
Long.bitCount如果元数据比较少,那么使用integer array,说是integer array其实不是很准确,因为integer array里面保存的是16位的数字,因为每个chunk上面每个integer的高16位是一样的,不需要重复存储,因此这个chunk占用的空间是: 16 * 元数据个数 + 16。这种容器背后的存储结构是一个动态的数组。
在前两种container都不是很高效的时候会采用Run Container(Run-length encoding里面的Run),如果元素个数多于4096,那么run的个数不能太多,如果元素的个数小于4096那么run的个数要小于cardinality的一半。Run容器的存储结构比较简单,它是一个数组,数组里面的每个元素是一对数字,第一个数字表示开始的数字,第二个数字表示长度,比如1,4表示的是1,2,3,4,5。
因为每个chunk的size最大只有8KB,因此它是可以被放进L1 Cache的,bitmap之间的intersection/union等等计算最后是在chunk之间的计算,因此能够放进L1 Cache会是一个很好的Cache有好的设计。
在实际的实现当中Roaring Bitmap是使用两个数组来实现roaring bitmap的: 一个array保存连续的chunk id -- 一个个16位的数字; 一个array保存对应的chunk容器。
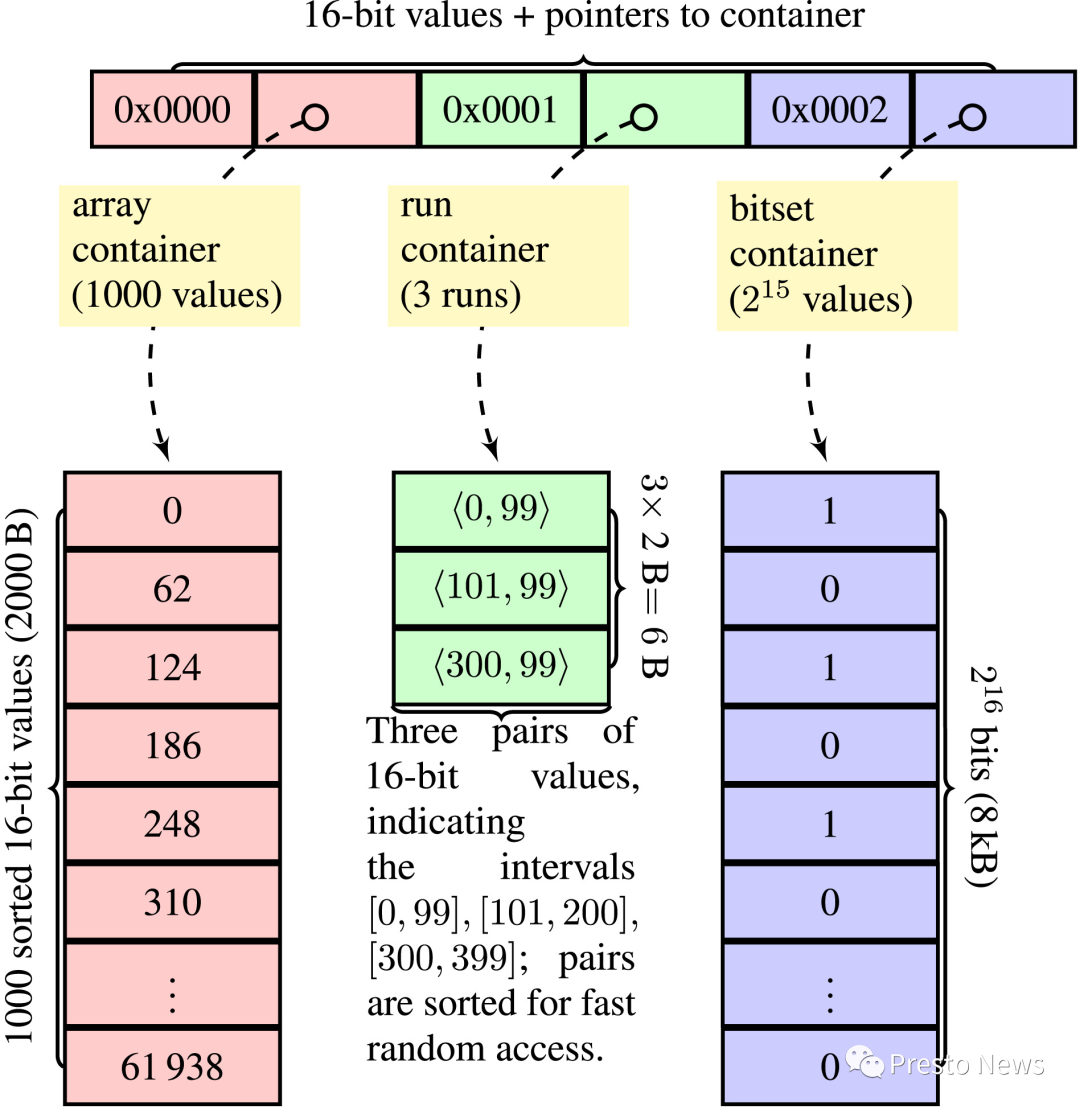
要检查一个元素是否在roaring bitmap里面是很快的,首先根据元素的值找到对应的chunk,因为chunk是按照固定的大小216 来切分的所以找到chunk是很快的;然后在到每个chunk对应的container里面去找:
如果底层是传统的bitmap,那么利用bit运算去check对应的bit是否为1即可。
如果底层是integer array的话,二分搜索对应的integer是否存在即可。
Roaring Bitmap的核心思想在于根据底层数据特征采用不同的容器类型,这种思想其实在很多其它问题领域都有看到。
Container之间逻辑运算
除了查找元素之外bitmap一些最重要的操作比如intersection/union是如何做的呢。Roaring Bitmap的这些操作其实最后的速度取决于底层container之间的相应的操作,下面就针对这些不同容器类型之间的各种操作简单说明一下。
bitmap VS bitmap
intersection
先通过bitCount操作对两个bitmap的intersection结果进行检查,如果结果超过4096,那么使用一个bitmap来保存结果,否则使用array来保存结果。
然后再通过bitwise运算再算一遍把结果保存到结果的container里面去。
注意这里其实计算了两遍,一遍为了计算元素的个数,一个计算实际的值,而这个整个的性能很大程度上取决于这个bitCount操作是否有指令级别的支持。
union操作是类似的,只不过把位AND改成位OR就好了。
array VS bitmap
intersection
这种情况比bitmap VS bitmap要简单,因为array保存的元素肯定比bitmap要少,所以intersection的结果容器一定是用一个array来保存比较合适。
决定了结果容器类型之后,我们只要遍历array container,去看对应的元素在不在bitmap里面就好了,这也是一个高效的操作,因为bitmap里面的查找操作是很快的。
union也是很高效的,结果容器肯定是bitmap,先根据输入bitmap克隆一个结果bitmap容器出来,然后遍历array把所有的元素加入到结果里面就好了,也是一些位操作。
array VS array
intersection
两个array相交的结果一定是array,如果两个array的cardinality相近(c1/64 < c2 < 64c1), 那么使用一个普通的merge算法,复杂度是O(c1 + c2);否则的话会使用一种叫做galloping intersection的算法,它的复杂度是 O(min(c1, c2)logmax(c1, c2))。
所谓的galloping intersection是用来求两个array的交集的时候使用的,而且这两个array的大小相差比较大。galloping算法遍历小array里面的每个元素,然后去大array进行binary search。
galloping intersection的一个缺点是会有很多的random内存访问(因为会做binary search),但是roaring bitmap里面使用这个算法的场景是多个container之间,而每个container最多8KB,两个container也只有16KB,是完全可以放在L1 cache里面,因此可以规避这个问题。
union
对于union如果两个array的cardinality的和大于4096,那么使用一个array来存,否则的话用一个bitmap来存。
虽然简单的把cardinality相加是不准的,但是如果结果是大于4096的,会先用一个bitmap来存,然后计算结果,如果最终结果小于4096, 会被转成一个array的。
run VS run
run和run之间的计算其实是比较straightfroward的。
run VS array
intersection
首先结果的container类型一定是array,因为是intersection,结果的个数不可能超过输入的array,也就更不可能包含更多的run。
算法本身就是挨个对比,略过不表。
union
run和array的union结果到底是什么类型不容易判断。论文里面对这个问题采用了run和run的unino的一样的算法,当得到结果之后再决定是否做container类型的转化。
run VS bitmap
intersection
首先第一步check run的cardinality
如果小于4096就初始化一个array作为结果container。然后依次check run里面的每个元素看是否存在于bitmap里面,并且输出到结果array里面。
如果超过4096就克隆一下input的bitmap container作为结果container,然后用很快的bitwise的操作来把run container里面的位补设为0,最后再根据结果的cardinality决定是否要把结果container转化成array。
union
先克隆一下输入的bitmap作为结果container。
然后利用很快的bitwise OR操作把run里面元素对应的位置设为1。
感想
看完整个论文,其实没有特别惊天动地的创新,但是让我很快想到了另外一个软件那就是Clickhouse,优化的思想很类似,不是有什么革命性的思想,但是对每种不同的场景选择最好的算法/容器(bitmap/array/runs), 再加上对于新硬件/指令(SIMD, popcnt)的合理应用最后得到了很好的结果。
参考资料
论文本身: https://arxiv.org/pdf/1603.06549.pdf
Faster intersections between sorted arrays with shotgun: https://lemire.me/blog/2019/01/16/faster-intersections-between-sorted-arrays-with-shotgun/
Roaring Bitmaps (January 2016): https://www.slideshare.net/lemire/roaring-bitmaps-january-2016






