在使用遗传算法前,可以利用参数Gepo_threshold的数值来调整触发的条件。为了方便代码解读,将这个边界条件降低至4(即RelOptInfo数量或者说基表数量为4的时候就尝试使用遗传算法)。下面在解读代码的过程中,以t1,t2,t3,t4四个表为例进行说明。
RelOptInfo作为遗传算法的基因,首先需要进行基因编码,openGauss数据库采用实数编码的方式,也就是用{1,2,3,4}分别代表t1,t2,t3,t4这4个表。
然后通过gimme_pool_size函数来获得种群的大小,种群的大小受Geqo_pool_size和Geqo_effort两个参数的影响,种群用Pool结构体进行表示,染色体用Chromosome结构体来表示。代码如下:
/* 染色体Chromosome结构体 */
typedef struct Chromosome {
/* string实际是一个整型数组,它代表基因的一种排序方式,也就对应一棵连接树 */
/* 例如{1,2,3,4}对应的就是t1 JOIN t2 JOIN t3 JOIN t4 */
/* 例如{2,3,1,4}对应的就是t2 JOIN t3 JOIN t1 JOIN t4 */
Gene* string;
Cost worth; /* 染色体的适应度,实际上就是路径代价 */
} Chromosome;
/* 种群Pool结构体 */
typedef struct Pool {
Chromosome *data; /* 染色体数组,数组中每个元组都是一个连接树 */
int size; /* 染色体的数量,即data中连接树的数量,由gimme_pool_size生成 */
int string_length; /* 每个染色体中的基因数量,和基表的数量相同 */
} Pool;
另外通过gimme_number_generations函数来获取染色体交叉的次数,交叉的次数越多则产生的新染色体也就越多,也就更可能找到更好的解,但是交叉次数多也影响性能,用户可以通过Geqo_generations参数来调整交叉的次数。
在结构体中确定的变量如下。
(1) 通过gimme_pool_size确定的染色体的数量(Pool.size)。
(2) 每个染色体中基因的数量(Pool.string_length),和基表的数量相同。
然后就可以开始生成染色体,染色体的生成采用的是Fisher-Yates洗牌算法,最终生成Pool.size条染色体。具体的算法实现如下:
/* 初始化基因序列至{1,2,3,4} */
for (i = 0; i < num_gene; i++)
tmp[i] = (Gene)(i + 1);
remainder = num_gene - 1; /* 定义剩余基因数 */
/* 洗牌方法实现,多次随机挑选出基因,作为基因编码的一部分 */
for (i = 0; i < num_gene; i++) {
/* choose value between 0 and remainder inclusive */
next = geqo_randint(root, remainder, 0);
/* output that element of the tmp array */
tour[i] = tmp[next]; /* 基因编码 */
/* and delete it */
tmp[next] = tmp[remainder]; /* 将剩余基因序列更新 */
remainder--;
}
表6-18是生成一条染色体的流程,假设4次的随机结果为{1,1,1,0}。
表6-18 生成染色体的流程
| 基因备选集 Tmp | 结果集 tour | 随机数 范围 | 随机数 | 说明 |
| 1 2 3 4 | 2 | 0~3 | 1 | 随机数为1,结果集的第一个基因为tmp[1],值为2,更新备选集tmp,将未被选中的末尾值放在前面被选中的位置上 |
| 1 4 3 | 2 4 | 0~2 | 1 | 随机数为1,结果集的第二个基因为4,再次更新备选集tmp |
| 1 3 | 2 4 3 | 0~1 | 1 | 随机数为1,结果集的第三个基因为3,由于末尾值被选,无须更新备选集 |
| 1 | 2 4 3 1 | 0~0 | 0 | 最后一个基因为1 |
在多次随机生成染色体后,得到一个种群,假设Pool种群中共有4条染色体,用图来描述其结构,如图6-13所示。
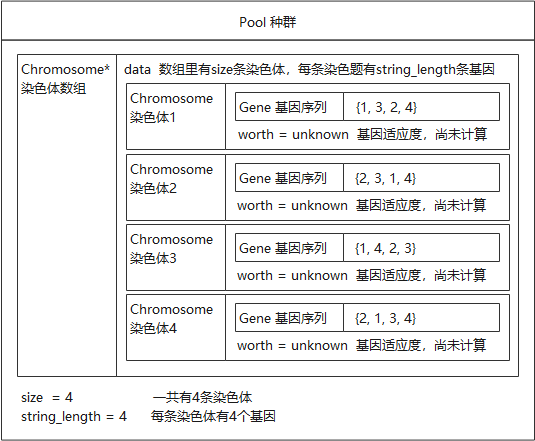
图6-13 染色体结构
然后对每条染色体计算适应度(worth),计算适应度的过程实际上就是根据染色体的基因编码顺序产生连接树,并对连接树求代价的过程。
在openGauss数据库中,每个染色体都默认使用的是左深树,因此每个染色体的基因编码确定后,它的连接树也就随之确定了,比如针对{2, 4, 3, 1}这样一条染色体,它对应的连接树就是(((t2,t4),t3), t1),如图6-14所示。
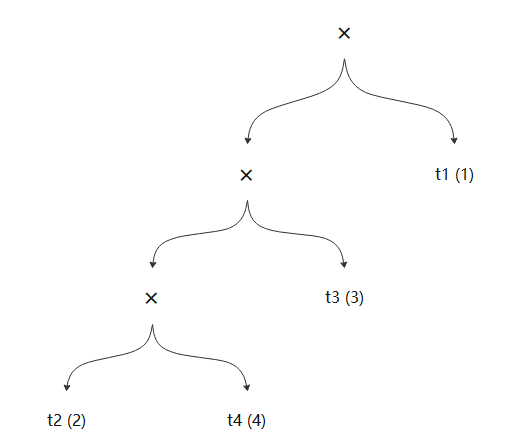
图6-14 染色体连接树
openGauss数据库通过geqo_eval函数来生成计算适应度,它首先根据染色体的基因编码生成一棵连接树,然后计算这棵连接树的代价。
遗传算法使用gimme_tree函数来生成连接树,函数内部递归调用了merge_clump函数。merge_clump函数将能够进行连接的表尽量连接并且生成连接子树,同时记录每个连接子树中节点的个数。再将连接子树按照节点个数从高到低的顺序记录到clumps链表。代码如下:
/* 循环遍历所有的表,尽量将能连接的表连接起来 */
For (rel_count = 0; rel_count < num_gene; rel_count++) {
int cur_rel_index;
RelOptInfo* cur_rel = NULL;
Clump* *cur_clump = NULL;
/* tour 代表一条染色体,这里是获取染色体里的一个基因,也就是一个基表 */
cur_rel_index = (int) tour[rel_count];
cur_rel = (RelOptInfo *) list_nth(private->initial_rels, cur_rel_index - 1);
/* 给这个基表生成一个Clump,size=1代表了当前Clump中只有一个基表*/
cur_clump = (Clump*)palloc(sizeof(Clump));
cur_clump->joinrel = cur_rel;
cur_clump->size = 1;
/* 开始尝试连接,递归操作,并负责记录Clump到clumps链表 */
clumps = merge_clump(root, clumps, cur_clump, false);
}
以之前生成的{2, 4, 3, 1}这样一条染色体为例,并假定。
(1) 2和4不能连接。
(2) 4和3能够连接。
(3) 2和1能够连接。
在这些条件下,连接树生成的过程见表6-19。
表6-19 连接树生成过程
| 轮数 relcount | 连接结果集 clumps | 说明 |
| 初始 | NULL | 创建基因为2的节点cur_clump,cur_clump.size = 1 |
| 0 | {2} | 因为clumps == NULL,cur_clump没有连接表,将cur_clump直接加入clumps |
| 1 | {2},{4} | 创建基因为4的节点cur_clump,cur_clump.size = 1,将基因为4的cur_clump和clumps链表的里的节点尝试连接,因为2和4不能连接,节点4也被加入clumps |
| 2 | {2} | 创建基因为3的节点cur_clump,cur_clump.size = 1,遍历clumps链表,分别尝试和2、4进行连接,发现和4能进行连接,创建基于3和4的连接的新old_clumps节点,ols_clumps.size = 2,在clumps链表中删除节点4 |
| {3, 4} {2} | 用2和4连接生成的新的old_clumps作为参数递归调用merge_clump,用old_clumps和clumps链表里的节点再尝试连接,发现不能连接(即{3,4}和{2}不能连接),那么将old_clumps加入clumps,因为old_clumps.size目前最大,插入clumps最前面 | |
| 3 | {3, 4} | 创建基因为1的节点cur_clump,cur_clump.size = 1 遍历clumps链表,分别尝试和{3,4}、{2}进行连接,发现和2能进行连接,创建基于1和2的新old_clumps节点,ols_clumps.size = 2,在clumps链表中删除节点2 |
| {3, 4} {1, 2} | 用1和2连接生成的新的old_clumps作为参数递归调用merge_clump,用old_clumps和clumps链表里的节点尝试连接,发现不能连接,将old_clumps加入clumps,因为old_clumps.size = 2,插入clumps最后 |
结合例子中的步骤,可以看出merge_clumps函数的流程就是不断的尝试生成更大的clump。
/* 如果能够生成连接,则通过递归尝试生成节点数更多的连接 */
if (joinrel != NULL) {
…………
/* 生成新的连接节点,连接的节点数增加 */
old_clump->size += new_clump->size;
pfree_ext(new_clump);
/* 把参与了连接的节点从clumps连表里删除 */
clumps = list_delete_cell(clumps, lc, prev);
/* 以clumps和新生成的连接节点(old_clump)为参数,继续尝试生成连接 */
return merge_clump(root, clumps, old_clump, force);
}
根据上方表中的示例,最终clumps链表中有两个节点,分别是两棵连接子树,然后将force设置成true后,再次尝试连接这两个节点。
/* clumps中有多个节点,证明连接树没有生成成功 */
if (list_length(clumps) > 1) {
……
foreach(lc, clumps) {
Clump* clump = (Clump*)lfirst(lc);
/* 设置force参数为true,尝试无条件连接 */
fclumps = merge_clump(root, fclumps, clump, true);
}
clumps = fclumps;
}






