要理解ElasticSearch(简称ES)和数据库的区别,那我们就必须要先了解什么是搜索。明白了搜索是什么概念之后,我们才能对ES的要点重拳出击,否则后续有很多的细节点是想不清楚的。还记得我当初我接触ES的时候,搜索的返回结果里面存在一个boost值,为什么会存在一个字段,这是用来干啥的,到底有啥用?后来我了解了什么是打分,我才知道boost是用来提升查询时候的权重的。诸如此类的基础知识还有很多,下面慢慢介绍。
本文分为如下几个部分:
搜索是什么? 搜索的原理 搜索的优化
搜索是什么?
在明确搜索是什么之前,我们需要先了解一个知识点:什么是信息检索(Information Retrieve 简称IR)。
信息检索是用户进行信息查询和获取的主要方式,是查找信息的方法和手段。狭义的信息检索仅指信息查询(Information Search)。即用户根据需要,采用一定的方法,借助检索工具,从信息集合中找出所需要信息的查找过程。广义的信息检索是信息按一定的方式进行加工、整理、组织并存储起来,再根据信息用户特定的需要将相关信息准确的查找出来的过程。又称信息的存储与检索。一般情况下,信息检索指的就是广义的信息检索。---- 百度百科
可以从定义上看出,搜索其实是信息检索的一个子集,而ES作为一个全文搜索引擎,它包含了数据的存储与检索,可以理解为是一个广义的信息检索引擎。
众所周知,Lucene是非常出名且高效的全文检索工具包,ES就是构筑在Lucene之上的,本文大部分的原理和算法都是通过研究Lucene来的。
搜索的原理
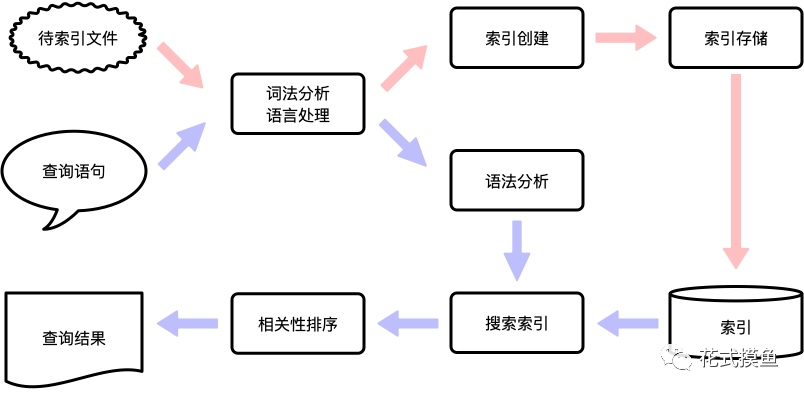
上图很简要的把搜索的原理展示了出来。会事先构建一个倒排索引,通过词法语法分析、分词、构建词典、构建倒排表、压缩优化等操作构建一个索引,查询时通过词典能快速拿到结果。但是,Lucene是如何做到在上亿条数据中准确找到我们需要的数据并且在毫秒级别的耗时中返回给我们的呢?
分词
分词,顾名思义,就是对一段文本,通过某种规则或者算法切分成多个词,分词后的每个词作为搜索项可以被搜索出来。这就意味着,如果分词粒度过大或过小,都有可能导致文本中明明存在这个词,但是死活却没办法被出现的情况。所以说恰如其分的分词是极为重要的!
举个例子好了:“这是一只灰色的大狼狗”,这该如何分词?当然我做为一个小学毕业语文考试考满分的人来说,这个分词很简单:“这”,“是”,“一只”,“灰色”,“的”,“大”,“狼狗”。但是我们现在来看几个错误的分词案例。
“这”,“是”,“一”,“只灰色”,“的大”,“狼狗”【错误语义】 “这是一只”,“灰色的大狼狗”【这分词太粗,搜索灰色就会找不到】 “这“,”是“,”一“,”只“,”灰“,”色“,”的“,”大“,”狼“,”狗”【分词太细了,搜啥都可能出来,比如搜色狼】
如何兼顾分词的准确性和粒度,就需要NLP的知识了,这里就不展开叙述。当然对于分词来说,还有很多操作可以做:
停用词(StopWord):很多语句中的词都是没有意义的,比如 “的”,“在” 等副词、谓词,英文中的 “a”,“an”,“the”,在搜索是无任何意义的,所以在分词构建索引时都会去除,降低不不要的索引空间。
归一化:USA - U.S.A. [缩写] 7月30日 - 7/30 [中英文] color - colour [通假词] 开心 - 高兴 [同义词扩展范畴]
词形归并(Lemmatization)
am, are, is -> be car, cars, car's, cars' -> car the boy's cars are different colors -> the boy car be different color
词干还原(Stemming) automate(s), automatic, automation -> automat. 高高兴兴 -> 高兴 [中文重叠词还原] 明明白白 -> 明白
倒排索引
一句话总结:
正排索引:一个未经处理的数据库中,一般是以文档ID作为索引,以文档内容作为记录。 倒排索引:Inverted index,指的是将单词或记录作为索引,将文档ID作为记录,这样便可以方便地通过单词或记录查找到其所在的文档。
用下面这个例子可以很好的理解什么是倒排索引:原始文档:
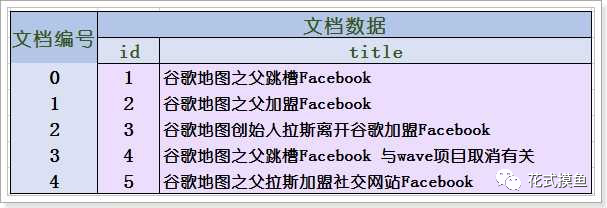
倒排索引:

搜索的过程 当用户输入任意的词条时,首先对用户输入的数据进行分词,得到用户要搜索的所有词条,然后拿着这些词条去倒排索引列表中进行匹配。找到这些词条就能找到包含这些词条的所有文档的编号。然后根据这些编号去文档列表中找到文档
下图可以很好的展示出Lucene中索引的存储结构
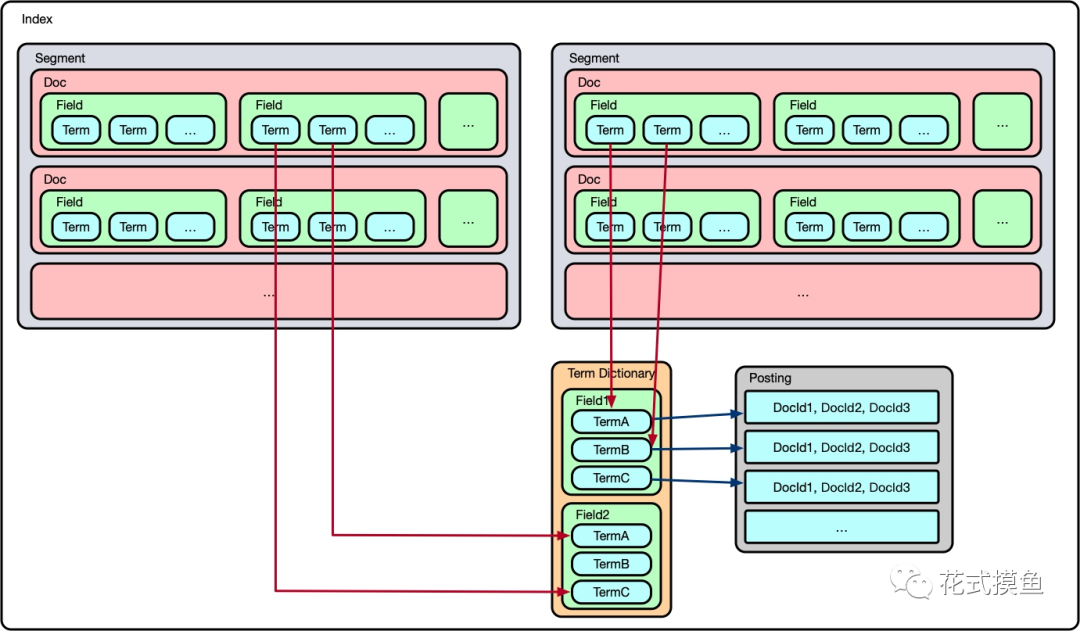
在Lucene中,从大到小是Index -> Segment -> Doc -> Field -> Term,类比 MySQL 为 Database -> Table -> Record -> Field -> Value。
查询结果排序
搜索结果排序是根据 关键字 和 Document 的相关性得分排序,通常意义下,除了可以人工的设置权重 boost,也存在一套非常有用的相关性得分算法。下面简单介绍介绍一下。
TF-IDF
TF-IDF(term frequency–inverse document frequency)是一种用于信息检索与数据挖掘的常用加权技术,常用于挖掘文章中的关键词,而且算法简单高效,常被工业用于最开始的文本数据清洗。
TF-IDF有两层意思,一层是"词频"(Term Frequency,缩写为TF),另一层是"逆文档频率"(Inverse Document Frequency,缩写为IDF)。
假设我们现在有一篇长文叫做《量化系统架构设计》词频高在文章中往往是停用词,“的”,“是”,“了”等,这些在文档中最常见但对结果毫无帮助、需要过滤掉的词,用TF可以统计到这些停用词并把它们过滤。当高频词过滤后就只需考虑剩下的有实际意义的词。
但这样又会遇到了另一个问题,我们可能发现"量化"、"系统"、"架构"这三个词的出现次数一样多。这是不是意味着,作为关键词,它们的重要性是一样的?事实上系统应该在其他文章比较常见,所以在关键词排序上,“量化”和“架构”应该排在“系统”前面,这个时候就需要IDF,IDF会给常见的词较小的权重,它的大小与一个词的常见程度成反比。
当有TF(词频)和IDF(逆文档频率)后,将这两个词相乘,就能得到一个词的TF-IDF的值。某个词在文章中的TF-IDF越大,那么一般而言这个词在这篇文章的重要性会越高,所以通过计算文章中各个词的TF-IDF,由大到小排序,排在最前面的几个词,就是该文章的关键词。
BM25
BM25算法,通常用来作搜索相关性评分。一句话概况其主要思想:对Query进行语素解析,生成语素qi;然后,对于每个搜索结果D,计算每个语素qi与D的相关性得分,最后,将qi相对于D的相关性得分进行加权求和,从而得到Query与D的相关性得分。
详细介绍可以看这篇文章 https://www.jianshu.com/p/1e498888f505
空间索引
使用过ES的同学都知道,ES是可以支持地理位置信息的索引的,丢进去一个经纬度,可以快速将索引中相邻的经纬度查询出来。其中的实现便是GeoHash。
GeoHash将二维的经纬度转换成字符串,比如下图展示了北京9个区域的GeoHash字符串,每一个字符串代表了某一矩形区域。
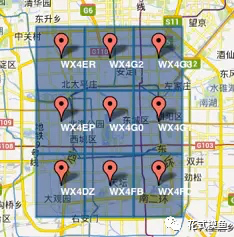
也就是说,这个矩形区域内所有的点(经纬度坐标)都共享相同的GeoHash字符串,这样既可以保护隐私(只表示大概区域位置而不是具体的点),又比较容易做缓存,比如左上角这个区域内的用户不断发送位置信息请求数据,由于这些用户的GeoHash字符串都是WX4ER,所以可以把WX4ER当作key,把该区域的位置信息当作value来进行缓存,而如果不使用GeoHash的话,由于区域内的用户传来的经纬度是各不相同的,很难做缓存。
字符串越长,表示的范围越精确。如图所示,5位的编码能表示10平方千米范围的矩形区域,而6位编码能表示更精细的区域(约0.34平方千米)
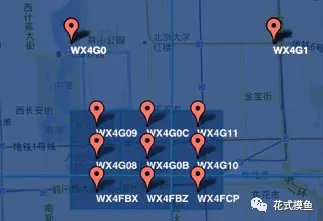
字符串相似的表示距离相近,这样可以利用字符串的前缀匹配来查询附近的POI信息。如下两个图所示,第一个在城区,第二个在郊区,城区的GeoHash字符串之间比较相似,郊区的字符串之间也比较相似,而城区和郊区的GeoHash字符串相似程度要低些。
那GeoHash是如何编码的呢?
地球纬度区间是[-90,90], 北海公园的纬度是39.928167,可以通过下面算法对纬度39.928167进行逼近编码: 区间[-90,90]进行二分为[-90,0),[0,90],称为左右区间,可以确定39.928167属于右区间[0,90],标记为1;接着将区间[0,90]进行二分为 [0,45),[45,90],可以确定39.928167属于左区间 [0,45),标记为0; 递归上述过程39.928167总是属于某个区间[a,b]。随着每次迭代区间[a,b]总在缩小,并越来越逼近39.928167; 如果给定的纬度x(39.928167)属于左区间,则记录0,如果属于右区间则记录1,这样随着算法的进行会产生一个序列1011100,序列的长度跟给定的区间划分次数有关。 将得到的编码进行组码,奇数位放经度,偶数位放纬度,每5个二进制编码一个十进制数,再利用base32进行编码得到对应的编码
由上述过程我们可以很轻松就的得到坐标(116.397 ,39.908)的编码值为(11010 01011,10111 00011),组码为11100 11101 00100 01111,base32编码值为WX4G。后续我们就可以拿着这个编码去做一些位置匹配的事情了。其实GeoHash还是有一些缺点的,这里就不展开描述了,有兴趣的同学可以自己查一查。
数值索引
Lucene的倒排索引决定,索引内容是一个可排序的字符串,如果要查找一个数字,那么也需要将数字转成字符串。这样,检索一个数字是没问题的,如果需要搜索一个数值范围,怎么做呢?
要做范围查找,那么要求数字转成的字符串也是有序并单调的,但数字本身的位数是不一样的,最简单的版本就是前缀补0,比如 35, 234, 1 都补成 4 位,得到 0035, 0234, 0001,这样能保证:
数字(a) > 数字(b) ===> 字符串(a) > 字符串(b)
这时候,查询应该用范围内的所有数值或查询,比如查询 [33, 36) 这个范围,对应的查询语法是:
33 || 34 || 35
嗯看起来很好的解决了范围查询,但是,这样存在3个问题:
补位多少合适呢?总有一个数字会超出你的补位范围 因为存在补位,就会多出很多的空间,这在搜索引擎里宝贵的内存是无法接受的 如果是范围查询,需要用多次或查询,性能并不高 故,涉及到范围不能简单的做字符串补位转换,是否存在及节省空间,又能更高效解决问题的方案呢?答案当然存在,那就是数值Trie树。大家只要记住Trie树的是hash树的变种,其原理是利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,能在常数时间O(len)内实现插入和查询操作,是一种以空间换取时间的数据结构就够了。
想要详细了解Trie树可以查看链接:https://segmentfault.com/a/1190000008877595
搜索的优化
LSM思想
如果大家有看过Google的BigTable的论文,相信对其中涉及到的LSM(Log Structured Merge Tree)一点都不陌生。LSM树的核心特点是利用顺序写来提高写性能,但因为分层(此处分层是指的分为内存和文件两部分)的设计会稍微降低读性能,但是通过牺牲小部分读性能换来高性能写,使得LSM树成为非常流行的存储结构。
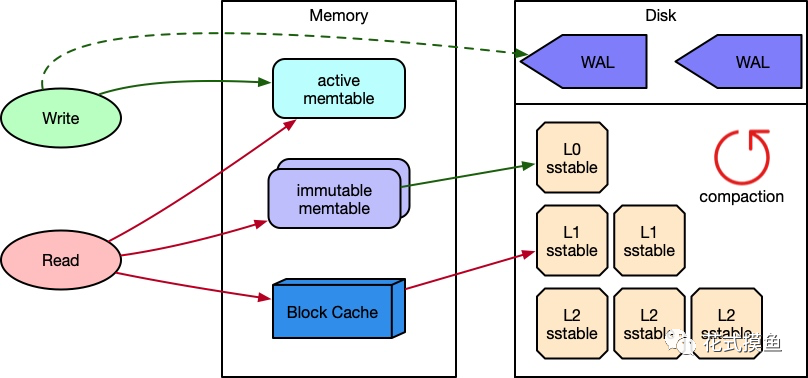
如上图所示,LSM树有以下三个重要组成部分:
MemTable
MemTable是在内存中的数据结构,用于保存最近更新的数据,会按照Key有序地组织这些数据,LSM树对于具体如何组织有序地组织数据并没有明确的数据结构定义,例如HBase使跳表来保证内存中key的有序。
因为数据暂时保存在内存中,内存并不是可靠存储,如果断电会丢失数据,因此通常会通过WAL(Write-ahead logging,预写式日志)的方式来保证数据的可靠性。
Immutable MemTable
当 MemTable达到一定大小后,会转化成Immutable MemTable。Immutable MemTable是将转MemTable变为SSTable的一种中间状态。写操作由新的MemTable处理,在转存过程中不阻塞数据更新操作。
SSTable(Sorted String Table)
有序键值对集合,是LSM树组在磁盘中的数据结构。为了加快SSTable的读取,可以通过建立key的索引以及布隆过滤器来加快key的查找。
这里需要关注一个重点,LSM树(Log-Structured-Merge-Tree)正如它的名字一样,LSM树会将所有的数据插入、修改、删除等操作记录(注意是操作记录)保存在内存之中,当此类操作达到一定的数据量后,再批量地顺序写入到磁盘当中。这与B+树不同,B+树数据的更新会直接在原数据所在处修改对应的值,但是LSM数的数据更新是日志式的,当一条数据更新是直接append一条更新记录完成的。这样设计的目的就是为了顺序写,不断地将Immutable MemTable flush到持久化存储即可,而不用去修改之前的SSTable中的key,保证了顺序写。
有关LSM的compaction操作可以看这篇文章,这里就不再赘述。https://zhuanlan.zhihu.com/p/181498475
Lucene的Segment设计思想,与LSM类似但又有些不同,继承了LSM中数据写入的优点,但是在查询上只能提供近实时而非实时查询。
Segment在被flush或commit之前,数据保存在内存中,是不可被搜索的,这也就是为什么Lucene被称为提供近实时而非实时查询的原因。读了它的代码后,发现它并不是不能实现数据写入即可查,只是实现起来比较复杂。原因是Lucene中数据搜索依赖构建的索引(例如倒排依赖Term Dictionary),Lucene中对数据索引的构建会在Segment flush时,而非实时构建,目的是为了构建最高效索引。当然它可引入另外一套索引机制,在数据实时写入时即构建,但这套索引实现会与当前Segment内索引不同,需要引入额外的写入时索引以及另外一套查询机制,有一定复杂度。
FST
lucene从4开始大量使用的数据结构是FST(Finite State Transducer)。FST有两个优点:
空间占用小。通过对词典中单词前缀和后缀的重复利用,压缩了存储空间 查询速度快。O(len(str))的查询时间复杂度。
下面简单描述下FST的构造过程(工具演示:http://examples.mikemccandless.com/fst.py?terms=&cmd=Build+it%21)。我们对“cat”、 “deep”、 “do”、 “dog” 、“dogs”这5个单词进行插入构建FST(注:必须已排序)。
1)插入“cat”
插入cat,每个字母形成一条边,其中t边指向终点。

2)插入“deep”
与前一个单词“cat”进行最大前缀匹配,发现没有匹配则直接插入,P边指向终点。
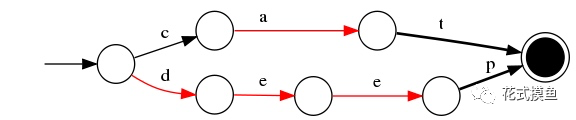
3)插入“do”
与前一个单词“deep”进行最大前缀匹配,发现是d,则在d边后增加新边o,o边指向终点。

4)插入“dog”
与前一个单词“do”进行最大前缀匹配,发现是do,则在o边后增加新边g,g边指向终点。
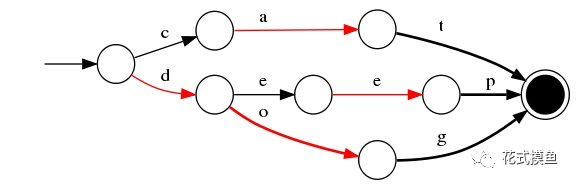
5)插入“dogs”
与前一个单词“dog”进行最大前缀匹配,发现是dog,则在g后增加新边s,s边指向终点。
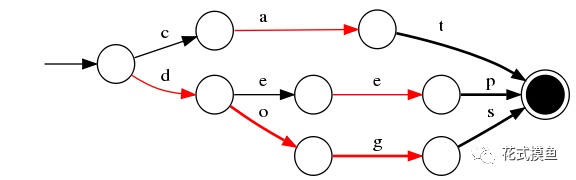
最终我们得到了如上一个有向无环图。利用该结构可以很方便的进行查询,如给定一个term “dog”,我们可以通过上述结构很方便的查询存不存在,甚至我们在构建过程中可以将单词与某一数字、单词进行关联,从而实现key-value的映射。
SkipList
为了能够快速查找docid,lucene采用了SkipList这一数据结构。SkipList有以下几个特征:
元素排序的,对应到我们的倒排链,lucene是按照docid进行排序,从小到大; 跳跃有一个固定的间隔,这个是需要建立SkipList的时候指定好,例如下图间隔; SkipList的层次,这个是指整个SkipList有几层

在什么位置设置跳表指针?
设置较多的指针,较短的步长, 更多的跳跃机会 更多的指针比较次数和更多的存储空间 设置较少的指针,较少的指针比较次数,但是需要设置较长的步长较少的连续跳跃
如果倒排表的长度是L,那么在每隔一个步长S处均匀放置跳表指针。
关于跳表的详细介绍,可以看这篇文章:https://www.jianshu.com/p/9d8296562806
小结
本文主要介绍了搜索引擎的实现原理以及其中涉及到的一些简单算法的介绍,当然只是挑选了其中比较实用且有意思的部分进行了介绍。关于搜索引擎的优化其实还有很多,比如BKD Tree,BitSet,IndexSorting等等。我在文末的参考文章中会附上我看的文章的链接。
参考文章:TF-IDF: https://zhuanlan.zhihu.com/p/31197209 BM25: https://www.jianshu.com/p/1e498888f505 LSM: https://zhuanlan.zhihu.com/p/181498475 FST: https://www.cnblogs.com/bonelee/p/6226185.html SkipList: https://www.jianshu.com/p/9d8296562806 BKD Tree: https://www.shenyanchao.cn/blog/2018/12/04/lucene-bkd/ BitSet: https://www.jianshu.com/p/bcded5fdc4c2 IndexSorting: https://blog.csdn.net/qq_27529917/article/details/108938201






