Mike Rosulek 课程系列(一)：安全多方计算

陆叁 2021-12-18

763

本文整理了美国俄勒冈州立大学电子工程和计算机科学学院的副教授Mike Rosulek关于安全多方计算与混淆电路的演讲主题的主要内容, 并进行了相关补充, 如有错误, 恳请批评指正.

安全多方计算的概念

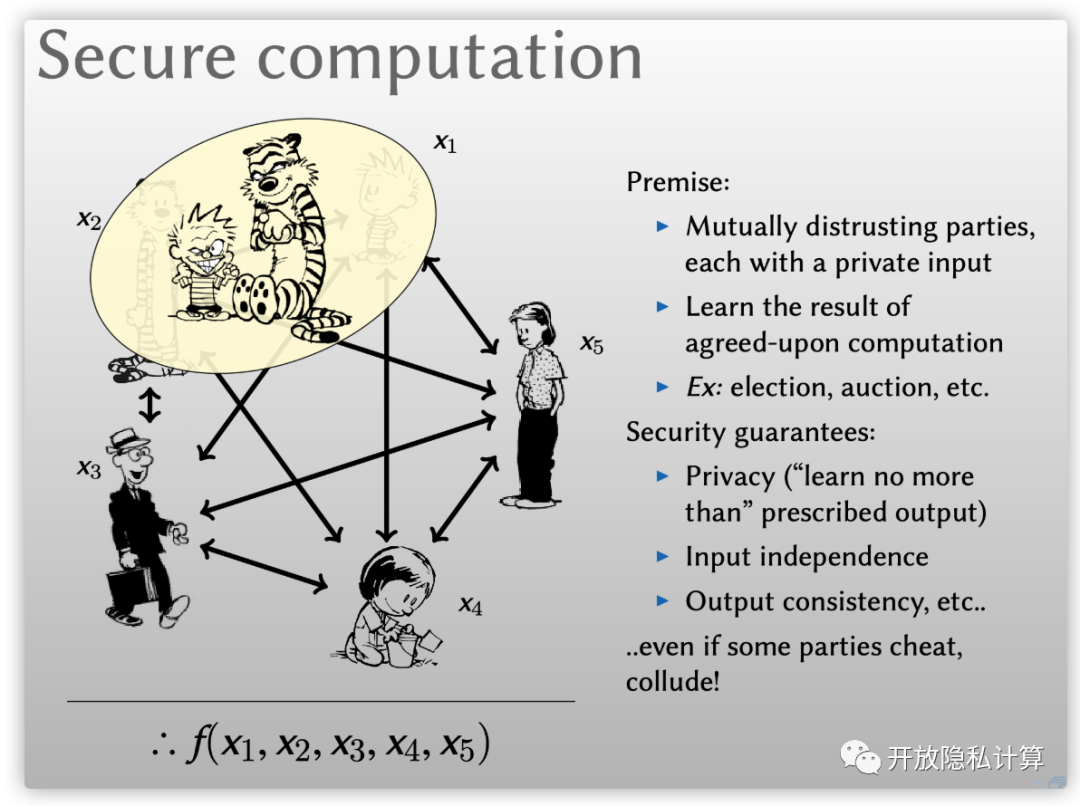
安全多方计算是指互不信任的分布式参与方拥有各自的隐私输入, 他们试图在不泄漏各自输入的前提下, 共同计算某个函数, 并获得不超出函数计算结果的输出. 常见的安全多方计算场景有选举、拍卖等. 由于参与方之间是互不信任的, 因此在安全多方计算中通常需要保证如下性质:

隐私性(Privacy): 这是最重要的一点, 任何参与方不能获得任何所规定的输出之外的信息;
输入独立性(Input independence): 各个参与方必须独立选择自己的输入, 即不能根据其他参与方的输入来选择自身的输入;
输出一致性(Output consistency): 如果某个参与方获得了输出, 则所有参与方都将获得相同的输出.
...

上述性质在某些参与方是作弊或者共谋的情形下仍需保持.

安全多方计算的现实应用

2009年起的丹麦使用安全多方计算来计算市场均衡时甜菜的价格, 并保证菜农和购买方无法得到关于对方心理价位的信息, 这是安全多方计算在现实世界中的一次大规模应用, 其他例子, 还有广告输入、2017年波士顿工资平等研究等等.

“安全”的含义

如何理解“安全地”计算 f 的含义? 不妨列举一下安全性所需属性问题:

如果敌手获得的信息不只有 f(x, y), 该怎么办?
如果敌手获得了f(x, y), 但阻止诚实参与方获得它, 该怎么办?
如果敌手迫使多个参与方的输出不一致, 该怎么办?
如果敌手选取的输入取决于诚实参与方的输入, 该怎么办?
...

实际上, 我们不会通过列表来定义安全性需要满足的属性. 我们需要给安全计算的安全性下一个定义, 即理想世界与现实世界范式(Ideal-Real world paradigm). 考虑两个参与方Alice和Bob, 分别拥有自己的隐私输入 x 和 y , 他们想计算f(x, y). 在理想世界中, 他们只需将各自的输入发给可信第三方(Trusted Third Party, TTP), TTP计算并返回f(x, y) 给各参与方. 腐败参与方Bob在这个理想世界中: 可以选取任何输入y (但独立于输入 x); 除了能获f(x, y) 的计算结果之外, 不能获得其他信息; 让诚实参与方Alice获得f(x, y), 而不是任何其他结果, 因为TTP只会发送正确的计算结果给诚实参与方. 因此, 理想世界非常简单, 敌手不能在其中做任何有害(harmful)的事情. 通过理想-现实范式(Ideal-Real paradigm)来定义多方计算的安全性, 其安全目标是现实协议交互与理想世界交互一样安全, 即任何对于真实协议的“攻击”, 都可以在理想世界中实现“相同的效果”. 我们知道在理想世界中唯一会发生的事情是harmless, 这意味着, 在现实世界中攻击协议会发生的事情也是harmless. 通常攻击的“效果”指的是敌手可获得或者计算出关于诚实参与方的信息或对诚实参与方输出造成某些影响. 这样, 我们可以给多方计算协议安全下一个定义:

对于任何现实世界的敌手 A , 存在一个理想敌A' , 使得诚实参与方输出与敌手输出 (HonestOutput, AdvOutput) 的联合分布不可区分.

不失一般性, 通常在理想世界中, 假设存在一个模拟器 (Simulator) 模拟敌手与现实世界交互. 模拟器有两个任务:

发送看起来像来自诚实参与方的协议信息;
通过检查敌手的协议信息来提取(extract)输入.

半诚实安全性

半诚实(Semi-honest, 或称为被动passive, 诚实但好奇honest-but-curious)敌手是一种特殊情况:

给定输入, 敌手会诚实地遵循协议;
敌手可能会基于他的视图尝试获取相关信息;
无提取 (extract) 步骤, 仅在给定理想输入和输出的情形下模拟序列 (transcript).

2000年, Ran Canetti提出的通用可组合 (Universally Composable, UC) 框架, 详细介绍了协议的安全性证明, 相关内容读者可以参考Ran Canetti的这篇文章Universally Composable Security: A New Paradigm for Cryptographic Protocols, 这里不再做详细介绍.

Mike Rosulek 课程系列(一)：安全多方计算

安全多方计算的概念

安全多方计算的现实应用

“安全”的含义

半诚实安全性

相关链接

评论