1、前言
书接上回,在气候变化领域小波分析最经常使用的功能应该是查看时间序列是否具有一定的周期性,在这方面小波分析和功率谱有着一定的相似之处(关于功率谱可以查看这篇之前发布的推送常用气候统计方法(含源码及示例)中功率谱的源码进行学习和尝试)。由于Python社区一直注重代码开源,所以同一种目的一般都能找到多种方法进行实现。进行我们使用第二种方法--基于pywct库来进行一次和Python气象数据处理与绘图:小波变换-基于wavelets中一样的操作,看看两种方法是否能得到同样的结果。这种思路也可以用于验证代码和数据的准确性。
2、安装模块
PyCWT是一个用于连续小波谱分析的Python模块。它包括一个小波变换例程的集合和统计分析通过FFT算法。此外,该模块还包括交叉小波变换、小波相干性测试和样本脚本。
pycwt这个库在官方文档中没有提供conda的安装方法,官网推荐使用pip进行安装,另外还要保证安装好numpy、scipy和matplotlib等库才能进行本文的其他操作。
1pip install pycwt复制
后续我在conda中搜索了一下,发现pycwt提供了安装方法,大家可以进行尝试。这里再说一下就是conda可以直接把pycwt需要的其他库也一并安装好,同时解决一些库版本高低的问题,我个人比较推荐使用conda。
由于众所周知的一些原因,国内连接conda官方源进行安装一些又不太好的体验,但是使用清华源的话又存在着一些库更新不及时以及很多库索引不到的情况。我个人还是比较推荐使用官方源,只要安装成功后就不会有一些其他的问题。
1conda install -c conda-forge pycwt
2conda install -c conda-forge/label/gcc7 pycwt
3conda install -c conda-forge/label/cf201901 pycwt
4conda install -c conda-forge/label/cf202003 pycwt复制
3、导入各种库
与上一篇文章中使用一样的数据来进行验证,首先我们导入相关的库,如果此时不报错的话就可以确保PyCWT已经正确安装在系统中了。
1from __future__ import division
2import numpy
3from matplotlib import pyplot
4import pycwt as wavelet
5from pycwt.helpers import find复制
4、导入数据

1url = 'http://paos.colorado.edu/research/wavelets/wave_idl/nino3sst.txt'
2dat = numpy.genfromtxt(url, skip_header=19)
3title = 'NINO3 Sea Surface Temperature'
4label = 'NINO3 SST'
5units = 'degC'
6t0 = 1871.0
7dt = 0.25 # In years复制
然后我们接着创建一个numpy格式的时间序列
11N = dat.size
22t = numpy.arange(0, N) * dt + t0复制
以下代码,通过标准偏差对输入数据进行去趋势化和规范化。有时去趋势化是不必要的,简单地去均值就足够了。但是,如果你的数据集有一个明确的趋势,比如莫纳罗亚二氧化碳数据集,强烈建议执行去趋势。这里,我们拟合一个一次多项式函数,然后从原始数据中减去它。
1p = numpy.polyfit(t - t0, dat, 1)
2dat_notrend = dat - numpy.polyval(p, t - t0)
3std = dat_notrend.std() # Standard deviation
4var = std ** 2 # Variance
5dat_norm = dat_notrend / std # Normalized dataset复制
下一步是定义小波分析的一些参数。我们选择了母小波,在这种情况下是ω0=6的Morlet小波。
1wave, scales, freqs, coi, fft, fftfreqs = wavelet.cwt(dat_norm, dt, dj, s0, J, mother)
2iwave = wavelet.icwt(wave, scales, dt, dj, mother) * std复制
计算归一化小波和傅里叶功率谱,以及每个小波尺度的傅里叶等效周期。
1power = (numpy.abs(wave)) ** 2
2fft_power = numpy.abs(fft) ** 2
3period = 1 / freqs复制
另外,我们还可以根据Liu et al.(2007)[2]提出的建议对功率谱进行校正
1power /= scales[:, None]复制
5、数据处理
1signif, fft_theor = wavelet.significance(1.0, dt, scales, 0, alpha,
2 significance_level=0.95,
3 wavelet=mother)
4sig95 = numpy.ones([1, N]) * signif[:, None]
5sig95 = power / sig95复制
2.然后计算全局小波谱并确定其显著性水平。
1glbl_power = power.mean(axis=1)
2dof = N - scales # Correction for padding at edges
3glbl_signif, tmp = wavelet.significance(var, dt, scales, 1, alpha,
4 significance_level=0.95, dof=dof,
5 wavelet=mother)复制
3.接着计算2 ~ 8年的量表平均值及其显著性水平
1sel = find((period >= 2) & (period < 8))
2Cdelta = mother.cdelta
3scale_avg = (scales * numpy.ones((N, 1))).transpose()
4scale_avg = power / scale_avg # As in Torrence and Compo (1998) equation 24
5scale_avg = var * dj * dt / Cdelta * scale_avg[sel, :].sum(axis=0)
6scale_avg_signif, tmp = wavelet.significance(var, dt, scales, 2, alpha,
7 significance_level=0.95,
8 dof=[scales[sel[0]],
9 scales[sel[-1]]],
10 wavelet=mother)复制
6、画图
画图展示结果部分
最后,我们将结果绘制在四个不同的子图上,包括(i)原始序列异常和小波反变换;(ii)小波功率谱(iii)全局小波和傅里叶谱;(iv)范围平均小波谱。在所有的副图中,显著性水平要么用虚线表示,要么用填充的等高线表示。
1# Prepare the figure
2pyplot.close('all')
3pyplot.ioff()
4figprops = dict(figsize=(11, 8), dpi=72)
5fig = pyplot.figure(**figprops)
6
7# First sub-plot, the original time series anomaly and inverse wavelet
8# transform.
9ax = pyplot.axes([0.1, 0.75, 0.65, 0.2])
10ax.plot(t, iwave, '-', linewidth=1, color=[0.5, 0.5, 0.5])
11ax.plot(t, dat, 'k', linewidth=1.5)
12ax.set_title('a) {}'.format(title))
13ax.set_ylabel(r'{} [{}]'.format(label, units))
14
15# Second sub-plot, the normalized wavelet power spectrum and significance
16# level contour lines and cone of influece hatched area. Note that period
17# scale is logarithmic.
18bx = pyplot.axes([0.1, 0.37, 0.65, 0.28], sharex=ax)
19levels = [0.0625, 0.125, 0.25, 0.5, 1, 2, 4, 8, 16]
20bx.contourf(t, numpy.log2(period), numpy.log2(power), numpy.log2(levels),
21 extend='both', cmap=pyplot.cm.viridis)
22extent = [t.min(), t.max(), 0, max(period)]
23bx.contour(t, numpy.log2(period), sig95, [-99, 1], colors='k', linewidths=2,
24 extent=extent)
25bx.fill(numpy.concatenate([t, t[-1:] + dt, t[-1:] + dt,
26 t[:1] - dt, t[:1] - dt]),
27 numpy.concatenate([numpy.log2(coi), [1e-9], numpy.log2(period[-1:]),
28 numpy.log2(period[-1:]), [1e-9]]),
29 'k', alpha=0.3, hatch='x')
30bx.set_title('b) {} Wavelet Power Spectrum ({})'.format(label, mother.name))
31bx.set_ylabel('Period (years)')
32#
33Yticks = 2 ** numpy.arange(numpy.ceil(numpy.log2(period.min())),
34 numpy.ceil(numpy.log2(period.max())))
35bx.set_yticks(numpy.log2(Yticks))
36bx.set_yticklabels(Yticks)
37
38# Third sub-plot, the global wavelet and Fourier power spectra and theoretical
39# noise spectra. Note that period scale is logarithmic.
40cx = pyplot.axes([0.77, 0.37, 0.2, 0.28], sharey=bx)
41cx.plot(glbl_signif, numpy.log2(period), 'k--')
42cx.plot(var * fft_theor, numpy.log2(period), '--', color='#cccccc')
43cx.plot(var * fft_power, numpy.log2(1./fftfreqs), '-', color='#cccccc',
44 linewidth=1.)
45cx.plot(var * glbl_power, numpy.log2(period), 'k-', linewidth=1.5)
46cx.set_title('c) Global Wavelet Spectrum')
47cx.set_xlabel(r'Power [({})^2]'.format(units))
48cx.set_xlim([0, glbl_power.max() + var])
49cx.set_ylim(numpy.log2([period.min(), period.max()]))
50cx.set_yticks(numpy.log2(Yticks))
51cx.set_yticklabels(Yticks)
52pyplot.setp(cx.get_yticklabels(), visible=False)
53
54# Fourth sub-plot, the scale averaged wavelet spectrum.
55dx = pyplot.axes([0.1, 0.07, 0.65, 0.2], sharex=ax)
56dx.axhline(scale_avg_signif, color='k', linestyle='--', linewidth=1.)
57dx.plot(t, scale_avg, 'k-', linewidth=1.5)
58dx.set_title('d) {}--{} year scale-averaged power'.format(2, 8))
59dx.set_xlabel('Time (year)')
60dx.set_ylabel(r'Average variance [{}]'.format(units))
61ax.set_xlim([t.min(), t.max()])
62
63pyplot.show()复制
效果:
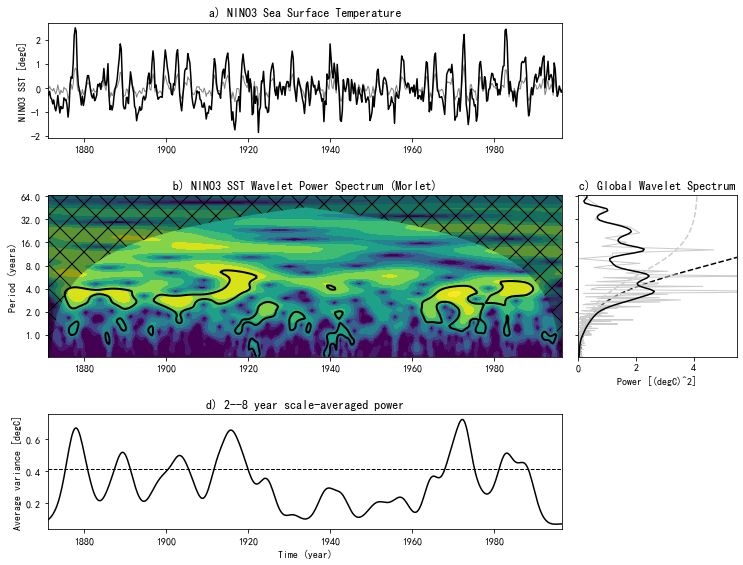
6、结果分析
NINO3海表温度记录的小波分析:(a)时间序列(实黑线)和小波反变换(实灰线),(b)采用Morlet小波(ω0=6)作为时间和傅里叶等效波周期(年)的函数对NINO3海表温度进行归一化小波功率谱分析。相对于红噪声随机过程(α=0.77),黑色实等高线所包含的区域可信度大于95%。交叉阴影区域表示受母小波影响的锥体的影响。(iii)全局小波功率谱(实黑线)和傅里叶功率谱(实灰线)。虚线表示95%置信水平。(iv) 2-8年尺度平均小波功率(实黑线)、功率趋势(实灰线)和95%置信水平(黑虚线)。
利用1871年开始Niño3海面温度和南方涛动指数进行研究,我们发现1880年、1920年和1960年和90年期间表现出显著的高功率,而在1920年和60年期间表现出较低的功率,以及可能的15年的方差调整。海平面气压功率Hovmöller在2-8年的小波功率在经度和时间上都存在显著的变化。
7、脚本和测试数据获取
在气海无涯公众号后台回复“小波分析2”,获取全部代码和测试数据。
有问题可以到QQ群里进行讨论,我们在那边等大家。








