推断统计分析(一)：python验证正态分布、大数定理、中值极限定理

推断统计分析：

• 推断统计分析(二)：python验证三大抽样分布
• 推断统计分析(三)：python实现假设检验

统计学是数据分析的基石，描述性统计分析：频率、频数、均值、中位数、众数、分位数、极差、方差、标准差等比较简单实现，就不多赘述，直接上推断统计分析的知识点。

本节先讲”参数估计“的相关概念“

• 一、正态分布
• 正态分布公式
• 正态分布特性
• 使用python验证正态分布
• 二、大数定理
• 什么是大数定理？
• python验证大数定理
• 三、中值极限定理
• 什么是中值极限定理？
• python验证中值极限定理

一、正态分布

• 正态分布公式

• 正态分布特性

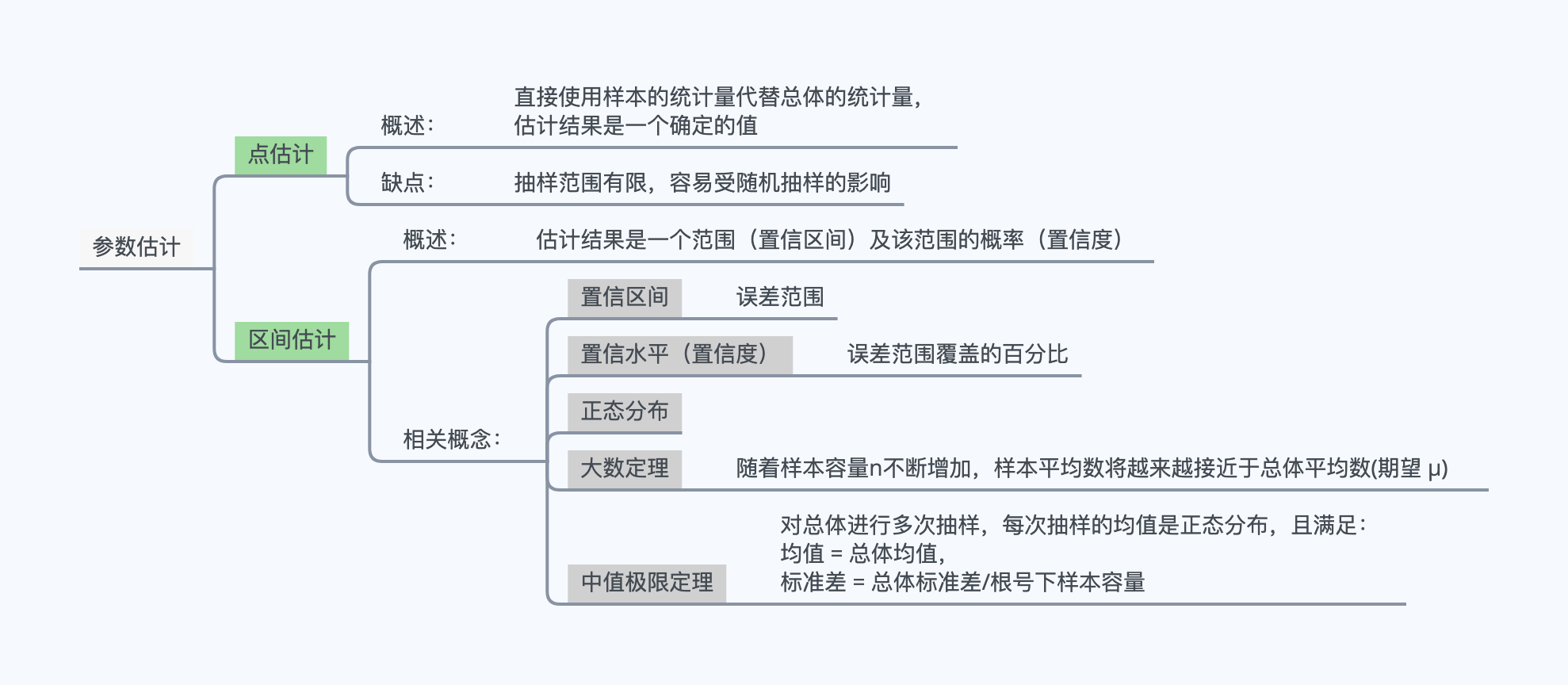
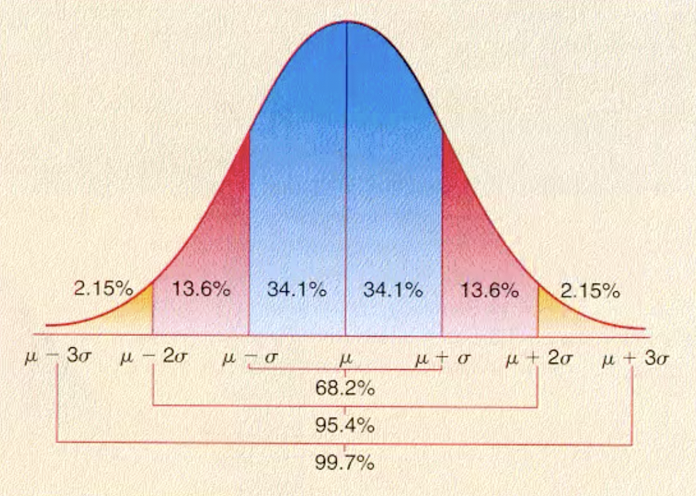
• 使用python验证正态分布

import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
import warnings

warnings.filterwarnings('ignore')  # 忽视warning的信息

sns.set(style='darkgrid')  # 设置绘图风格
plt.rcParams['font.family'] = 'Arial Unicode MS'  # 设置字体格式，支持中文
plt.rcParams['axes.unicode_minus'] = False  # 支持负号

# 生成一组均值为0，标准差为50的正态分布的数据
data = np.random.normal(0, 50, 1000000)

# 画个图看一下
sns.kdeplot(data, shade=True)
plt.axvline(x=data.mean(), ls="-", c="purple")# 添加垂直直线
plt.show()

下图即是生成的均值为0的1000000个数据的图形分布：

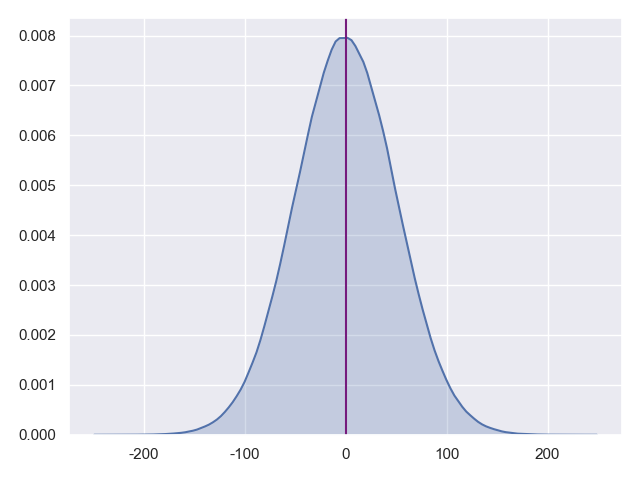
# 计算各个置信区间的置信度
for i in range(1, 4):
    target = data[(data >= 50*(-i)) & (data <= 50*i)]
    level = len(target) / len(data) * 100
    print('置信区间为正负{}倍标准差内,置信度为：{}%'.format(i, level))

ok,根据结果，再去对比正态分布特性，可以看出，结果基本符合。

二、大数定理

• 什么是大数定理？

随着样本容量n不断增加，样本平均数将越来越接近于总体平均数(期望 μ)

• python验证大数定理

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

#生成10万个值
all_value = np.random.randint(1,100000,100000)

#随机取100、200...个值的均值
sample_size = []
sample_maen = []
for i in range(100,100000,100):
    sample_size.append(i)
    sample_maen.append(np.random.choice(all_value,i).mean())
df = pd.DataFrame({"sample_size":sample_size,"sample_maen":sample_maen}).set_index("sample_size")
# 画个图看一下
df.plot()
plt.axhline(all_value.mean(),color = "red")
plt.show()

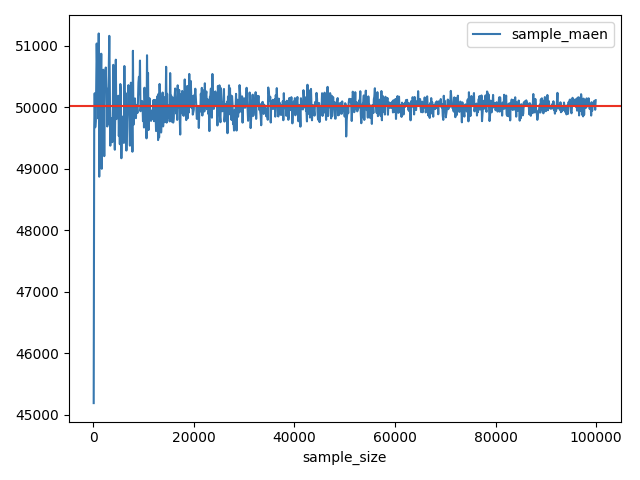
根据图形，我们可以清楚的看到，随着样本容量不断增加，样本的均值在总体的均值上下波动，且波动范围越来越小，越来越接近总体均值

三、中值极限定理

• 什么是中值极限定理？

1、多次抽样的均值呈正态分布
2、该正态分布的均值=总体均值
3、该正态分布的标准差/根号下样本容量 = 总体标准差

• python验证中值极限定理

''
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
import warnings
import pandas as pd

warnings.filterwarnings('ignore')  # 忽视warning的信息

sns.set(style='darkgrid')  # 设置绘图风格
plt.rcParams['font.family'] = 'Arial Unicode MS'  # 设置字体格式，支持中文
plt.rcParams['axes.unicode_minus'] = False  # 支持负号

# 生成一组均值为30，标准差为100的正态分布的数据
data = np.random.normal(30, 80, 100000)

# 随机抽取以上数据,每次抽64个，抽1000次
arr_mean = np.zeros(1000)
for i in range(1000):
    arr_mean[i] = np.random.choice(data, size=64, replace=False).mean()

print('样本组成的分布均值为：', arr_mean.mean())
print('样本组成的分布标准差为：', arr_mean.std())
print('样本组成的分布偏度为：', pd.Series(arr_mean).skew())

# 画个图
sns.kdeplot(arr_mean, shade=True)
plt.axvline(x=data.mean(), ls="-", c="purple", label='总体均值')
plt.axvline(x=arr_mean.mean(), ls="-", c="green", label='样本均值')
plt.legend()
plt.show()

先看一下输出结果：

总体均值我们设定的是30，样本组成的分布的均值是30.1，基本接近
总体标准差80，样本容量64，样本组成的分布的标准差是10.008，基本接近80/8
分布的偏度为0.0015接近于0，则表明为正态分布

我们再看一下输出的图形：

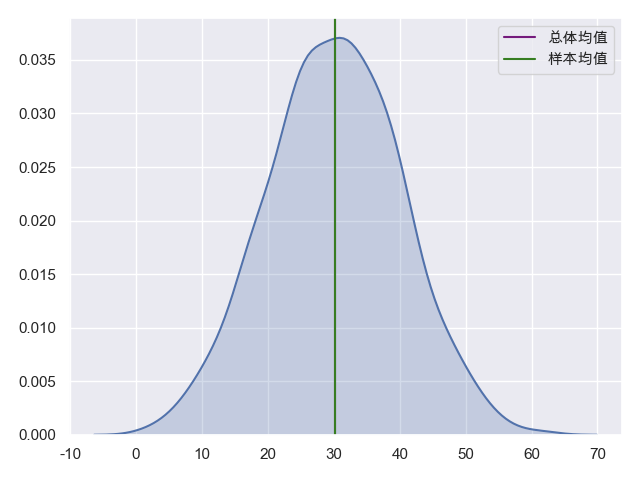
图形基本可以看做一个正态分布，且样本均值和总体均值，重合了，说明样本均值与总体均值几乎一致

OK，就这样，我们过了一遍正态分布、大数定理、中值极限定理，你学会了吗？