推断统计分析(二)：python验证三大抽样分布

推断统计分析：

• 推断统计分析(一)：python验证正态分布、大数定理、中值极限定理
• 推断统计分析(三)：python实现假设检验

抽样分布：从已知的总体中以一定的样本容量进行随机抽样，由样本的统计数所对应的概率分布称为抽样分布。抽样分布是统计推断的理论基础。

• 一、卡方分布
• 什么是卡方分布？
• 卡方分布与正态分布
• python验证卡方分布与正态分布的关系
• 二、T分布
• 什么是T分布？
• T分布与正态分布
• python验证T分布与正态分布的关系
• 三、F分布
• 什么是F分布？
• python绘制F分布的概率密度函数图象

一、卡方分布

• 什么是卡方分布？

若n个相互独立的随机变量ξ₁、ξ₂、……、ξn,均服从标准正态分布（也称独立同分布于标准正态分布），则这n个服从标准正态分布的随机变量的平方和构成一新的随机变量，其分布规律称为卡方分布（chi-square distribution）。

• 卡方分布与正态分布

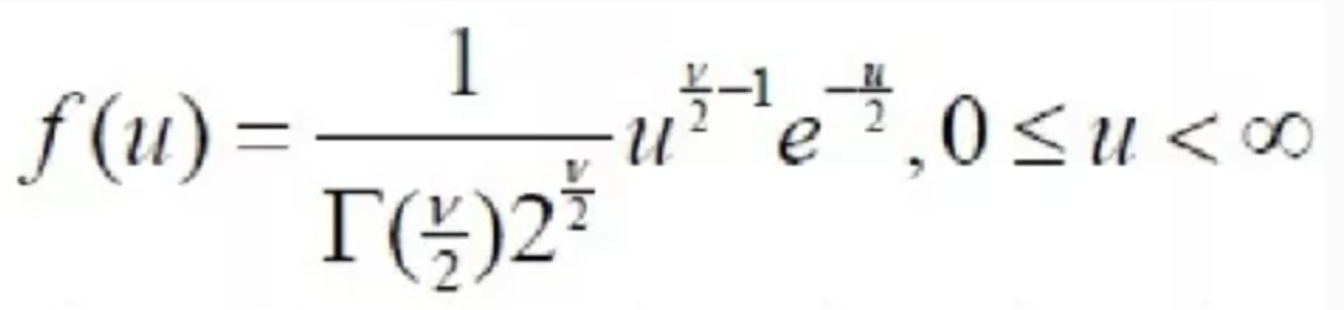
随着卡方分布样本容量的增加，卡方分布的概率密度曲线趋于对称。当样本容量n -> +∞的时候，卡方分布 -> 正态分布，即卡方分布的极限分布就是正态分布。

• python验证卡方分布与正态分布的关系

x = np.linspace(0, 100, 100000)
for i in range(10, 51, 10):
    y = stats.chi2.pdf(x, df=i)
    plt.plot(x, y, label='n={}'.format(i))
plt.title('卡方分布随样本容量增加的变化关系图')
plt.legend()
plt.show()

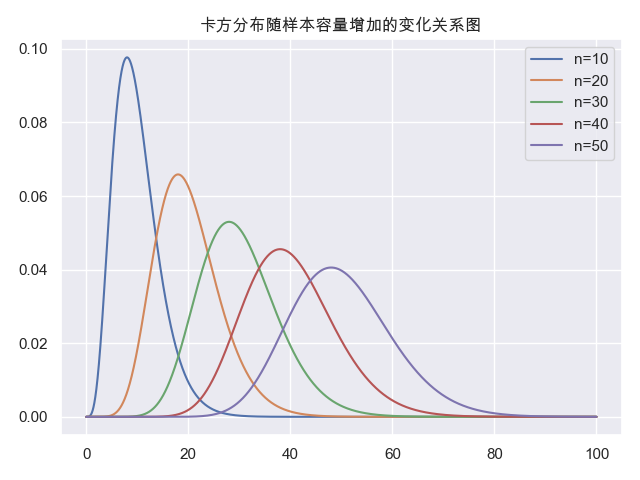
随着样本容量的增加，卡方分布的概率密度曲线趋于对称。样本容量越趋近于+∞，卡方分布越趋近于正态分布。

二、T分布

• 什么是T分布？

设X1服从标准正态分布N(0,1)，X2服从自由度为n的χ2分布，且X1、X2相互独立，则称变量t=X1(X2/n)1/2所服从的分布为自由度为n的T分布。

• T分布与正态分布

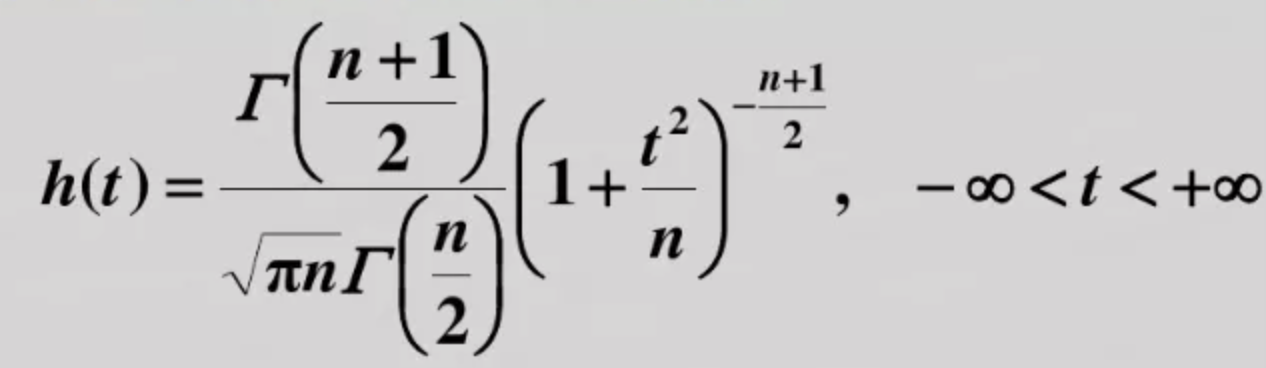
t分布的概率密度函数和正态分布的概率密度函数都是偶函数(左右对称的)。t分布随着样本容量的增加，就越来越接近正态分布，即t分布的极限分布也是正态分布。  
当样本容量在 30-35之间时，t分布与标准正态分布难以区分
当样本容量达到120时，t分布与标准正态分布实际上完全相同了

• python验证T分布与正态分布的关系

x = np.linspace(-3, 3, 100)
plt.plot(x, t.pdf(x, 1), label='df=1')
plt.plot(x, t.pdf(x, 30), label='df=2')
plt.plot(x, t.pdf(x, 120), label='df=120')
plt.plot(x[::5], norm.pdf(x[::5]), 'kx', label='normal')
plt.legend()
plt.title('t分布随样本容量增加的变化关系图')
plt.show()

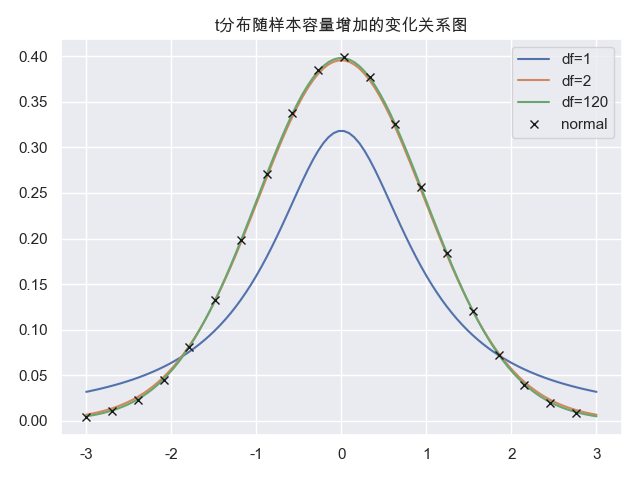
t分布一直是对称的，随着样本容量的增加，越来越趋近于正态分布，当样本容量到30时，t分布与标准正态分布难以区分，当样本容量达到120时，t分布与标准正态分布实际上完全相同了。

三、F分布

• 什么是F分布？

设X1服从自由度为m的χ2分布，X2服从自由度为n的χ2分布，且X1、X2相互独立，则称变量F=(X1/m)/(X2/n)所服从的分布为F分布，其中第一自由度为m，第二自由度为n。

• python绘制F分布的概率密度函数图象

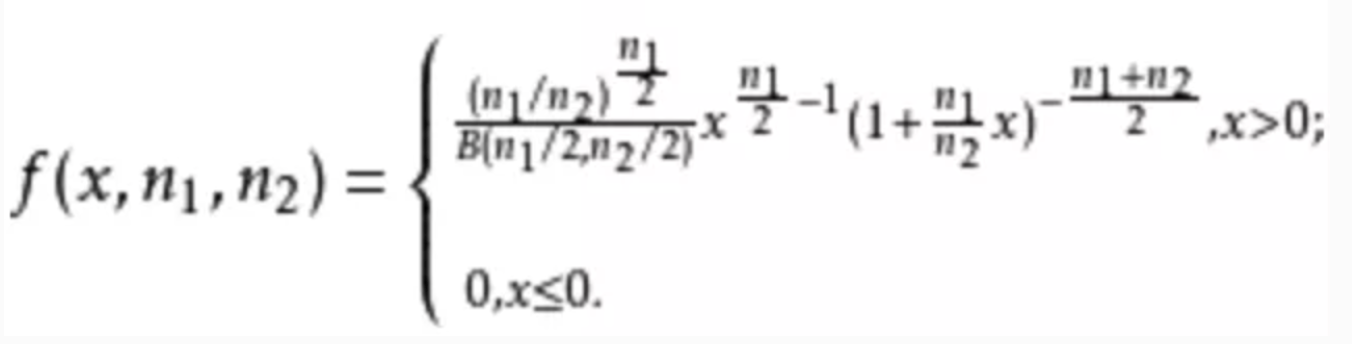
x = np.linspace(-1, 8, 100000)
plt.plot(x, stats.f.pdf(x, 1, 10), label='m=1, n=10')
plt.plot(x, stats.f.pdf(x, 5, 10), label='m=5, n=10')
plt.plot(x, stats.f.pdf(x, 100, 10), label='m=10, n=10')
plt.ylim(0, 1)
plt.title('F分布的概率密度函数')
plt.legend()
plt.show()

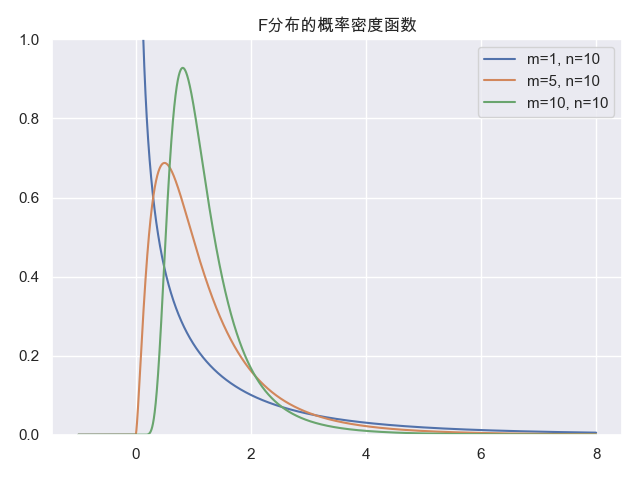
F分布是不对称的，随着样本容量的增加，图形并不会趋近于正态分布。