推断统计分析:
假设检验:通过正态分布、中值极限定理、参数估计等原理,推断样本与总体的差异
一、基础概念
进行假设检验之前,你必须先要了解一些假设检验的基础概念,比如:小概率事件、显著性水平、p-value等小概念。
另外,关于检验方式的选择、假设检验的步骤我也在这个导图中一并总结了。
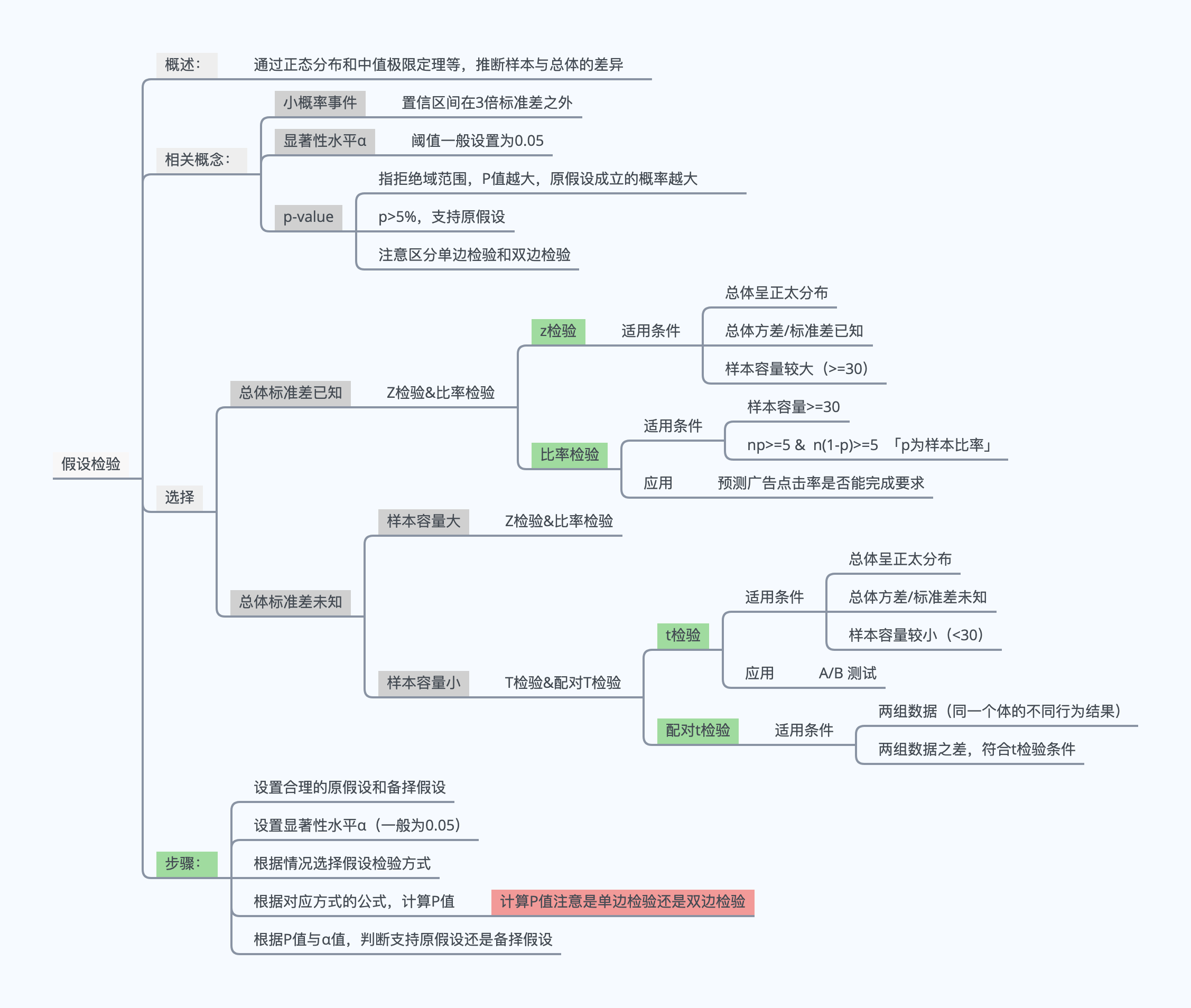
补充:什么是p-value?
p-value即为拒绝域,我们各种检验最终都是求拒绝域的大小,当拒绝域大于我们设置的阈值(显著性水平),那么置信水平就没有那么大了,那么就要放弃原假设,改而支持备择假设了。
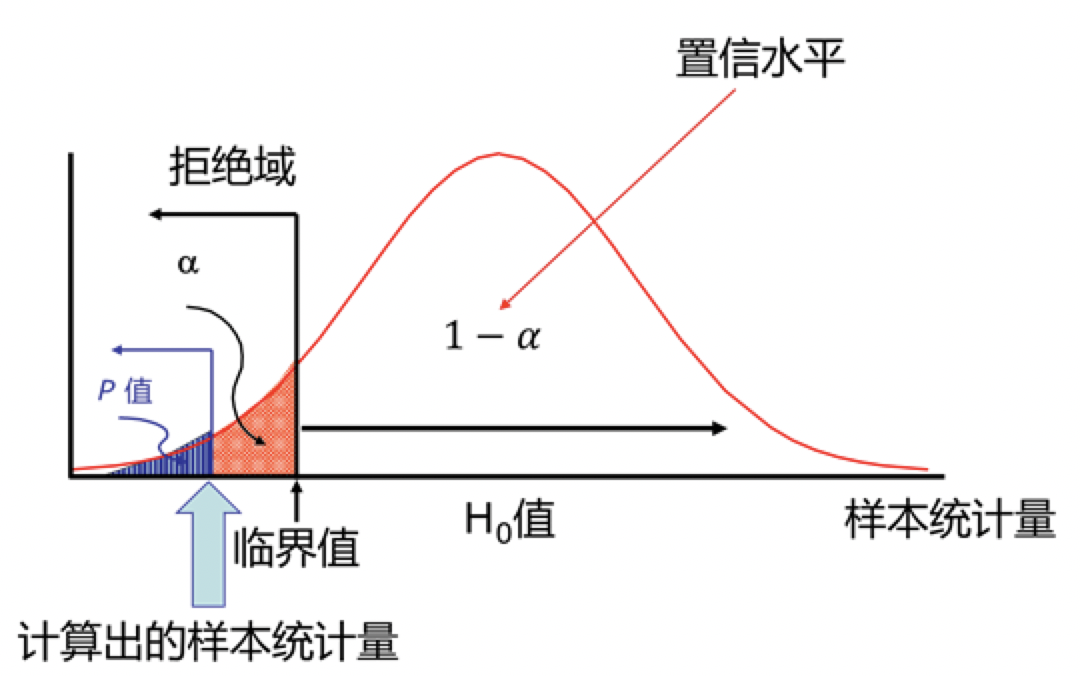
二、假设检验
看了上面基础理论知识,我们开始学习常见的这四种假设检验理论、应用场景以及python实现。
-
适用条件
1、总体呈正态分布
2、总体方差已知
4、样本容量较大(>=30) -
数学公式

- python实现案例
案例:检验牛奶是否掺水
已知条件:纯牛奶密度mean, std = -0.545, 0.08
假设检验:
1、原假设:mean >= -0.545 (掺水了);备择假设:mean <= -0.545 (没掺水)
2、显著性水平:α = 0.05
3、符合正太分布、标准差已知–>选择单边Z检验;
import numpy as np
from scipy import stats
# 买了10瓶牛奶,密度如下
data = np.array([-0.547, -0.532, -0.548, -0.531, -0.535])
# 总体均值,标准差
mean, std = -0.545, 0.008
# 样本均值
sample_mean = data.mean()
# 样本容量
sample_len = len(data)
# 计算Z统计值
Z = (sample_mean - mean) / (std / np.sqrt(sample_len))
print('Z值为:', Z)
# 计算P值
P = stats.norm.cdf(Z) # 牛奶掺水的拒绝域是牛奶没掺水,所以拒绝域在左边,使用cdf
print('P-value值为:', P)
alpha = 0.05
if P >= alpha:
print('支持原假设:牛奶掺水了')
else:
print('支持备择假设:牛奶没掺水')

-
适用条件
1、样本容量>=30
2、np>=5 且 (1-np)>=5 (p为样本比率) -
数学公式
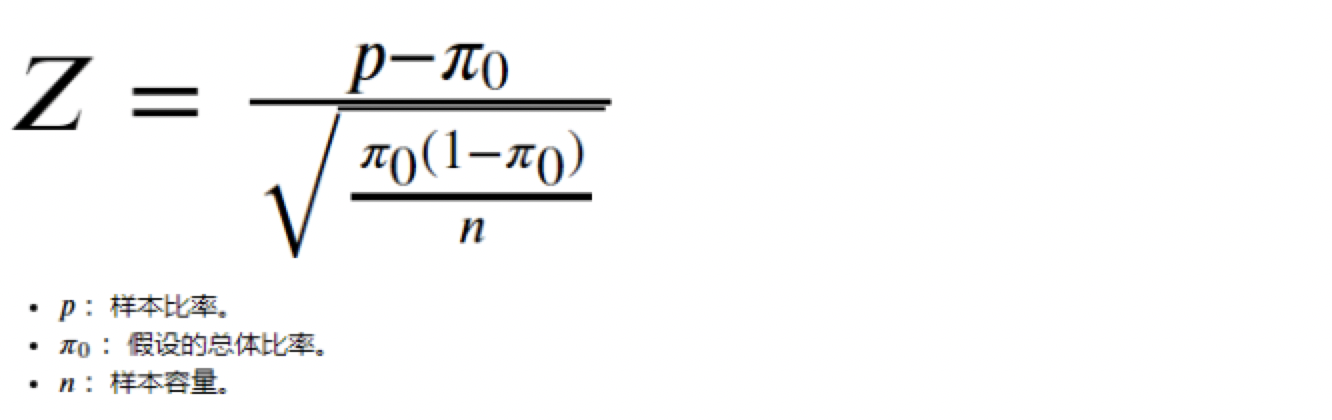
-
python实现案例
案例:广告优化后是否达到月均点击率10%的目标
已知条件:是否达到10%,即总体比率为10%
假设检验:
1、原假设:比率>= 10% (完成目标了);备择假设:比率< 10% (未完成目标)
2、显著性水平:α = 0.05
3、检验方式:单边比率检验
import numpy as np
from scipy import stats
# 总体比率
ratio = 0.1
# 样本比率(访问量是500,点击量是45)和样本容量
sample_ratio = 45 / 500
sample_len = 500
Z = (sample_ratio - ratio) / np.sqrt(ratio * (1 - ratio) / sample_len)
print('Z值为:', Z)
P = stats.norm.cdf(Z)
print('P值为:', P)
alpha = 0.05
if P >= alpha:
print('支持原假设:完成目标了')
else:
print('支持被择假设,没有完成目标')

-
适用条件
1、总体呈正态分布
2、总体方差未知
3、样本容量较小(<30) -
数学公式
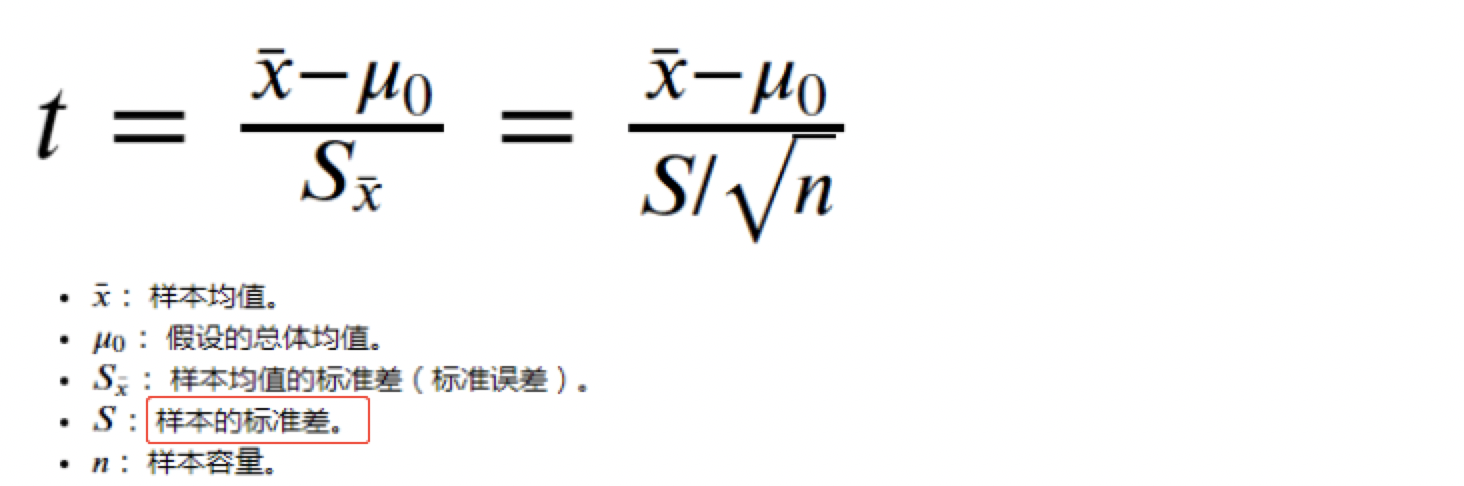
- python实现案例
案例:小刘是否完成月销售量50的任务目标
已知条件:目标均值50,即假设总体均值为50
假设检验:
1、原假设:mean >= 50 (完成了目标);备择假设:mean <= 50 (没完成目标)
2、显著性水平:alpha = 0.05
3、检验方式:符合正太分布、标准差未知–>单边T检验
import numpy as np
from scipy import stats
# 小刘最近一周的销售量如下
data = np.array([50, 48, 50, 47, 46, 48, 51])
# 总体均值
mean = 50
# 样本均值、标准差、容量
sample_mean = data.mean()
sample_std = data.std()
sample_len = len(data)
# T值
T = (sample_mean - mean) / (sample_std / np.sqrt(sample_len))
print('T值为:', T)
# P值
P = stats.t.cdf(T, df=sample_len-1) # 原假设是>(右边),所以拒绝域在左边,使用cdf
print('P值为:', P)
alpha = 0.05
if P >= alpha:
print('支持原假设:小刘完成了目标')
else:
print('支持备择假设:小刘未完成目标')

-
适用条件
1、符合t分布的条件
2、两组数据分别是受试者在处理前与处理后的数据 或者 受试者经过两种不同方式处理方式,产生的数据 -
数学公式

- python实现案例
案例:10名员工减肥是否有效果
已知条件:是否显著是看与0的差距,即总体均值假设为0
假设检验:
1、原假设:mean(after-before) <= 0 (有效果:有效果是体重降低,所以小于0);备择假设:mean(after-before)> 0 (没效果)
2、显著性水平:alpha = 0.05
3、检验方式:两组数之差满足T检验要求–>单边配对T检验
import numpy as np
from scipy import stats
# 员工减肥前&后体重
train_before = np.array([98.8, 92.0, 94.9, 101.2, 99.3, 85.1, 94.8, 89.2, 89.5, 92.1])
train_after = np.array([88.4, 92.4, 90.3, 88.4, 89.3, 89.0, 92.5, 87.4, 88.9, 85.4])
# 总体均值
mean = 0
# 计算差值
data = train_after - train_before
# 差值样本的均值和标准差和容量
sample_mean = data.mean()
sample_std = data.std()
sample_len = len(data)
# T值
T = sample_mean / (sample_std / np.sqrt(sample_len))
print('T值为:', T)
# P值
P = stats.t.sf(T, df=sample_len-1) # 原假设是>(左边),所以拒绝域在右边,使用sf
print('P值为:', P)
alpha = 0.05
if P >= alpha:
print('支持原假设:减肥有效果')
else:
print('支持被择假设,减肥没有效果')








