前几天解析了CSN 日志文件,今天我们来解析FSM文件,FSM的全称为Free Space Map,空闲空间映射文件,每个表文件都有一个对应的以_fsm为后缀的文件(如下图,另外一个以_vm为后缀的文件,我们下回解析),用来登记该表的每个数据块block所剩余的可用空间。
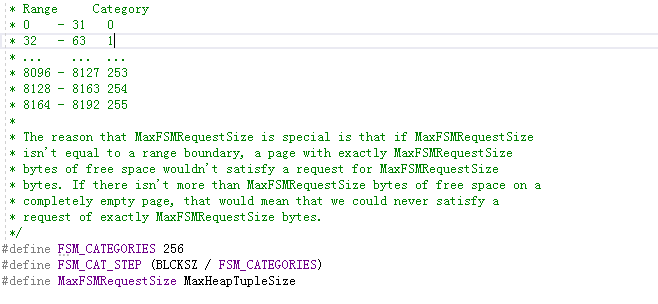
我们知道数据页的大小为8K=即8*2^10,如果需要精准表示每个页面的剩余空间的大小,至少需要14个bit位来存储,超过一个字节的大小。所以,openGauss/postgresql 采用稍微粗略的记录方式,将剩余空间分成256个档次, 用0表示剩余空间在0~31个字节范围之间,用1表示范围为32~63,,,,,,,,用255表示范围为8164~8192(如下图),采取这种方式,只需一个字节就可以表示一个block所剩空间的大小。
但是,一个FSM页面,真的可以登记8000多个block的剩余空间吗?答案是否定的。一个FSM页面到底可以登记多少个block的剩余空间信息?我们来解析源代码。
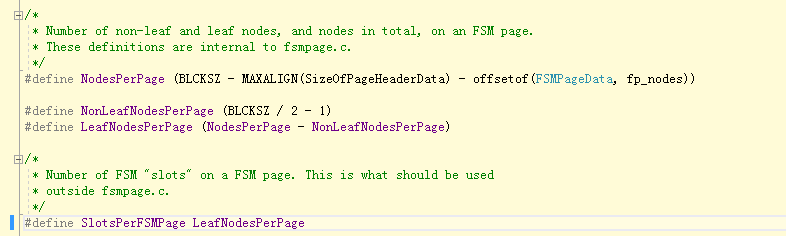
BLKSZ=8192
NodesPerPage :8192-40-4=8148
NonLeafNodesPerPage: 8192/2-1=4095
LeafNodesPerPage:8148-4095=4053
SlotsPerFSMPage=LeafNodesPerPage= 4053
通过以上计算,一个leaf 节点的FSM文件的block可以登记4053个表文件的block的剩余空间信息。我们简单计算一下,假如表文件有1024*1024个block(也就是8G),则需要FSM文件的block数量为1024乘1024除4053=258余2902,再加上一个父级,以及一个祖父级的fsm块,等于261个block,261*8192=2138112字节,大约需要2M的FSM空间,这个空间极小。
我们将表文件的块的剩余空间登记起来,目的是在需要空间的时候,快速找到满足空间要求的block. 这个又是如何实现的?
树形结构是适合用来查找的,FSM同样采用了这种机制。 前面我们讲过,一个FSM block可以存放4053个页面的剩余空间信息, 一个8G的表文件需要259个FSM Block来登记它们的剩余空间。 当在执行SQL的时候,需要找到一个满足空间要求的页面,如何在259页面中去找到一个满足条件的特定位点(一个字节宽度,记录着对应的一个表文件block的剩余空间)? 显然,我们需要将这些FSM页面按照一定规则组织起来,以便我们查找。
FSM页面具有层级结构,下面的代码是FSM页面的逻辑的数据结构。

用level属性表示该页面属于第几层级,用logpageno属性表示该页面属于该层级的第几个页面。因为typedef uint32 BlockNumber; 定义了blocknumer的类型是32位的无符号整数,而4053*4053*4053远超过2^32-1,所以FSM文件的组织层级为3级,从0开始计算,FSMAddress对象的level的属性最大值为2. 也就是根节点页面的level属性值为2,leaf 节点为0, 中间层节点为1.
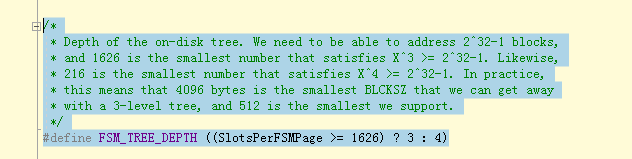
#define FSM_ROOT_LEVEL (FSM_TREE_DEPTH - 1), 也就是FMS页面的root节点页面的level为2.
FSM的root页面(节点)如何跟其下层页面之间建立关系的呢?我们继续看代码。

通过fsm_get_child函数中的这行代码, child.logpageno = parent.logpageno * SlotsPerFSMPage + slot;即一个父节点上的slot,可以换算成子节点上的一个页面号,即可以知道,父节点页面上的一个slot,管理(对应)的是子节点上一个页面,(该slot登记的信息是对应的子页面上所管理的4053个数据块的所剩空间的最大值,后面我们再讲到这块代码)。
这就是FSM文件块的层次结构。
但我们还没有讲,一个FSM页面,所登记的4053个页面的剩余空间信息,它们是如何组织的。 如果我们要去找到某个满足空间要求的页面,我们不能将这4053条空间信息挨个比对,直到找到满足条件的页面为止。如果是这样,那查找效率太差了,在追求高性能的数据库中,这样的代码是决对不允许存在的。
FSM页面内部的信息,采用的是二叉树的方式存放,以便快速查找到满足空间要求的页面(block)。

如上图,采用的是这样的二叉树来存放页面所剩空间的信息,父节点存放的是两个子节点中的最大的值,顶层记录的是整个树的最大的值。该二叉树采用数组来实现,因为页面中需要存储大量非叶子节点,这也就是为什么1个字节可以表示一个页面的剩余空间,但一个8k大小的FSM页面只能登记4053个页面的剩余空间,而不是8000多个页面。下面是fsm页面的数据结构,用一个数组fp_nodes来表示二叉树,前面NonLeafNodesPerPage(即4095)个元素是非叶子节点,后面才是叶子节点,登记了对应的数据页的剩余空间。非叶子节点元素里面记录的信息只是为了帮助实现快速查找,并非某个页面的剩余空间。
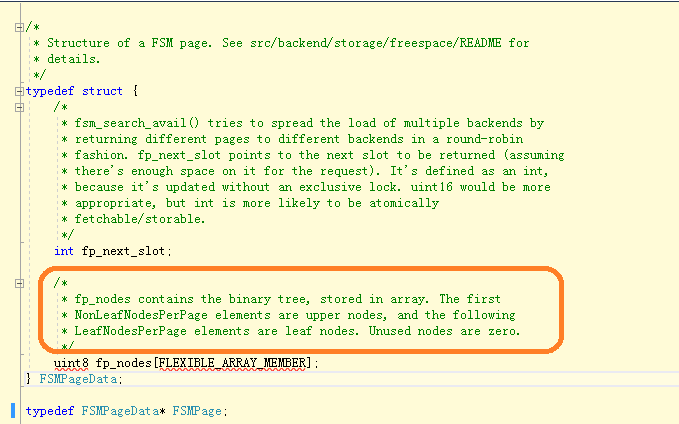
下面是在一个FSM页面内,查找满足空间要求的数据页面的函数。
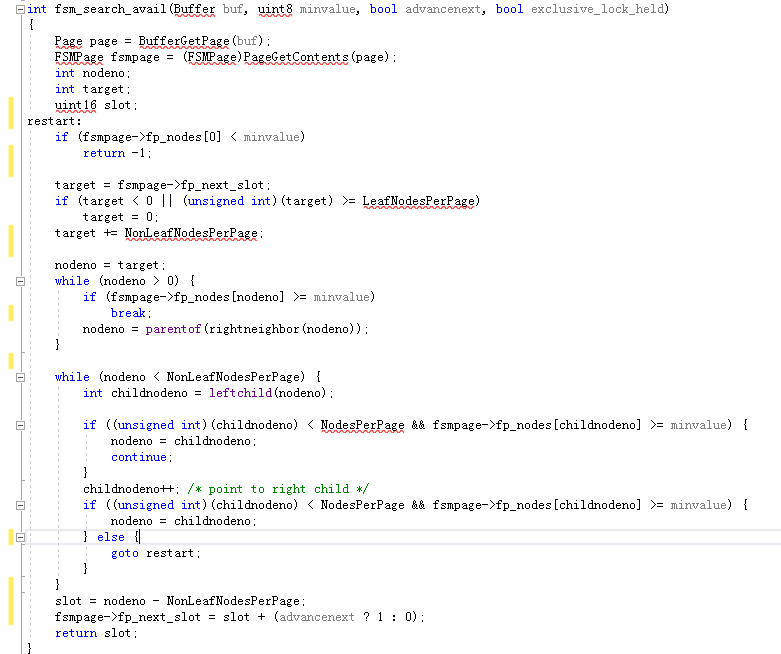
我们来解析这个fsm_search_avail函数:
if (fsmpage->fp_nodes[0] < minvalue)
return -1;
二叉树的根节点的值最大,如果根节点的值比要查找的值还小,说明这个FSM页面所管辖的数据页的所剩空间没有满足要求的, 直接退出。
然后从起点开始找,起点位置为fsmpage->fp_next_slot;
target = fsmpage->fp_next_slot;
如果起点位置不满足,开始攀爬,往上找(nodeno = parentof(rightneighbor(nodeno));)。代码如下:

直到找到满足要求的节点之后,因为该节点可能是非叶子节点(只要发生攀爬,就是非叶子节点),所以需要再往下探(往下探代码:int childnodeno = leftchild(nodeno);),具体代码如下。直到找到满足条件的叶子节点,然后查找完成。
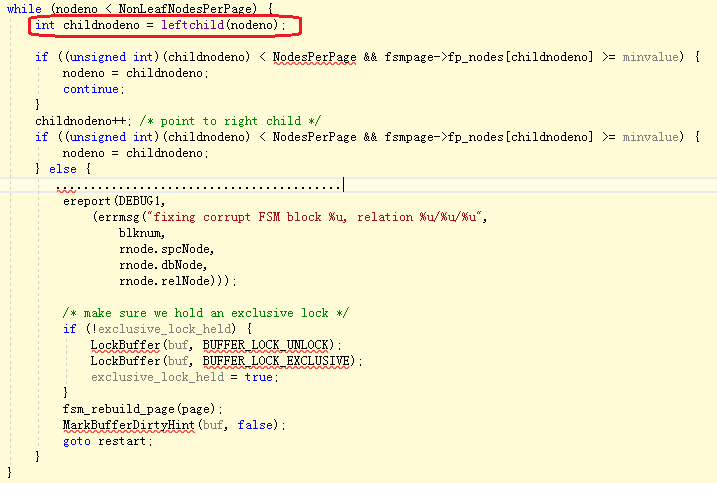
对于FSM文件的解析,到这里,核心功能应该说已基本介绍完毕。希望对读者朋友们理解这块内容有所帮助。






