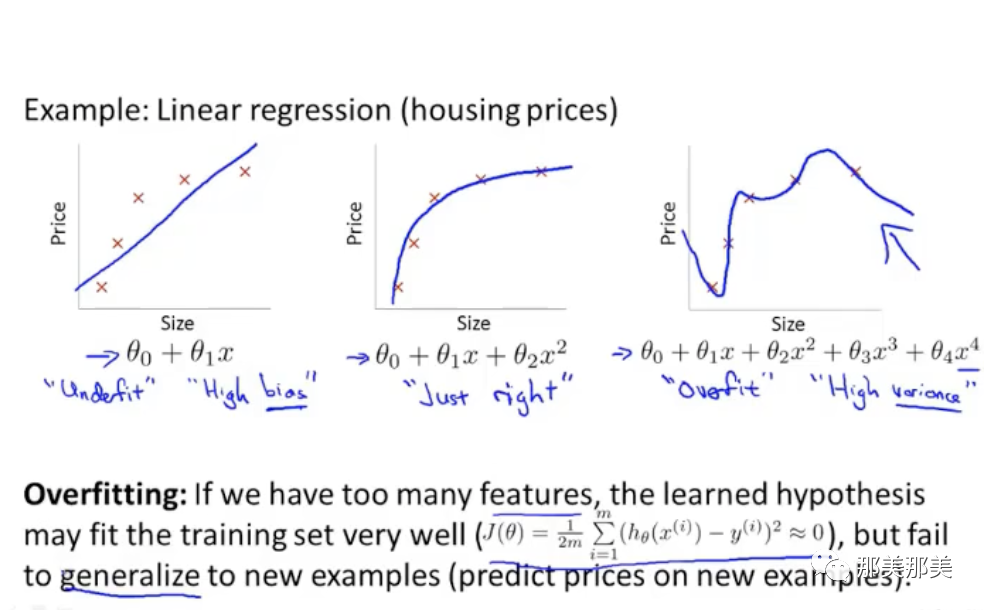
线型回归的欠拟合和过拟合问题.
逻辑回归的欠拟合和过拟合的问题.

过拟合即训练出来的h𝝷值能够将所有的样本进行区分,所得到的曲线极度扭曲此时J𝝷值趋近于0,无法很好地泛化到新的样本数据.
当我们样本数据的特征非常多,但训练数据非常少时,就会出现过拟合的情况.解决过拟合的问题,通常说来有两种方法:

1. 人工选择最相关的变量特征,但是有可能舍弃一些相关的特征.
2. 正则化来进行实现. 我们保留所有特征,但减少样本的数量级𝝷j的大小.
假设我们在J𝝷在后面加上惩罚变量1000 * 𝝷3^2, 1000 * 𝝷4^2,如果此时我们需要J𝝷得到最小化的值,那么我们只有令𝝷3、𝝷4趋于0,则这个时候的拟合就是一个曲线.𝝷3和𝝷4的值越小,此时越不容易出现过拟合的情况,曲线也就更平滑.
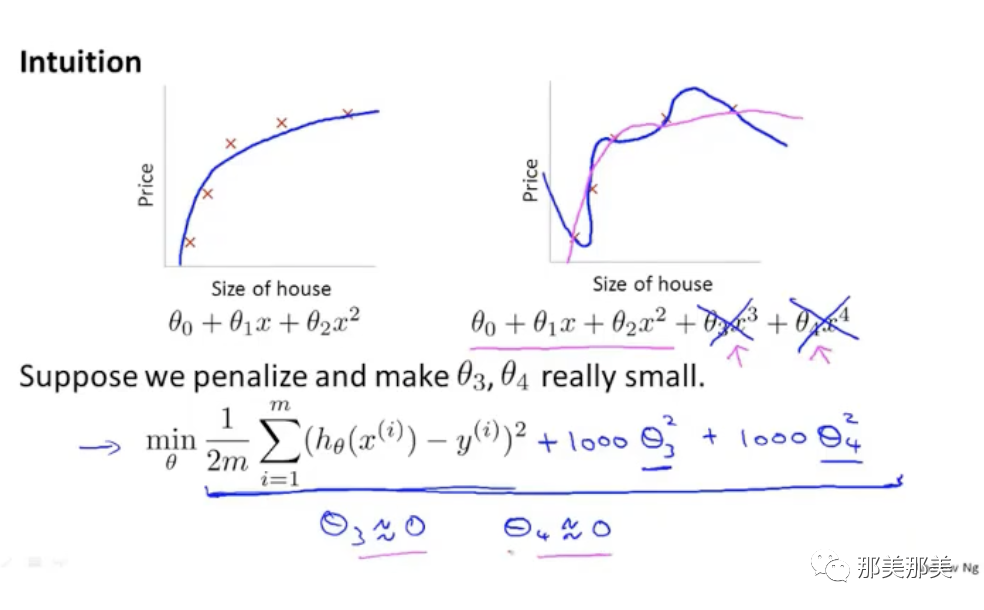
所以此时我们可以将J𝝷变为以下形式(因为我们根本不知道应该应该在那个𝝷上面加入惩罚函数,所以干脆全部加上).

如果设置正则化参数值过大,会导致出现𝝷1至𝝷4的值趋近于0, 才能使J𝝷的值最小化,则此时就出现了欠拟合的情况,因为此时的是𝝷0的值,即一条平行线.

线型回归和逻辑回归的正则化处理.

1-@ *y/m的值总是接近于1的一个数. 需要注意线型回归和逻辑回时的h𝝷(x)的含义是不同的,因为其预测函数是不同的.
为什么没有了𝝷^2 的表示,因为梯度下降的时候是对J𝝷的求偏导. 正则化函数是从𝝷1开始的,所以此时需要单独表示出𝝷0的过程.
文章转载自那美那美,如果涉嫌侵权,请发送邮件至:contact@modb.pro进行举报,并提供相关证据,一经查实,墨天轮将立刻删除相关内容。






